基础训练之“链表”

BM1  反转链表

 题意：给一个不带头节点的链表，将其翻转。

 题解：有以下几种思路

1. 新建一个头节点，然后使用头插法，将链表中的结点一个一个插入。
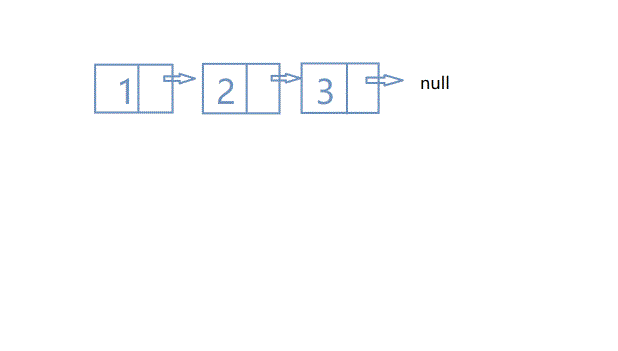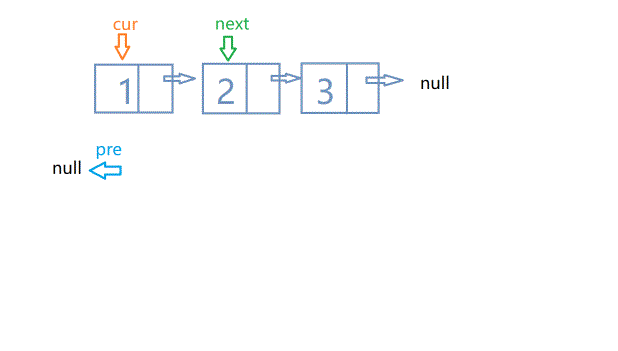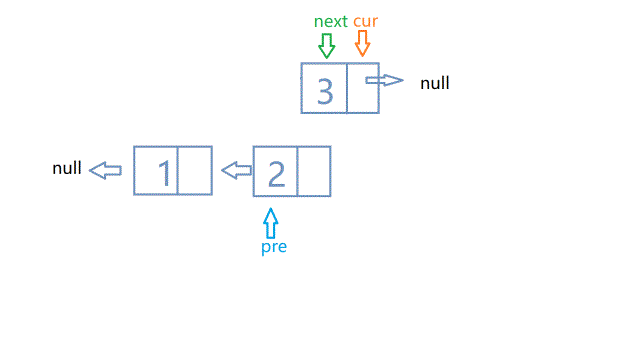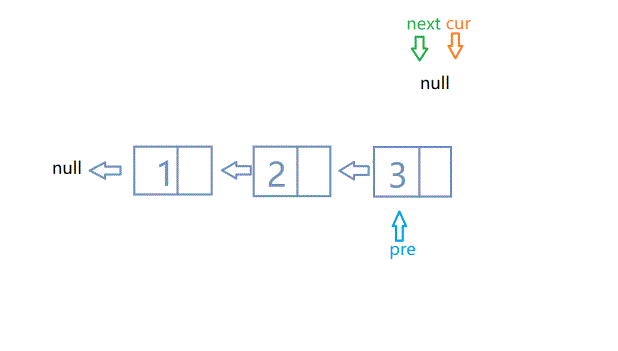
2. 原地进行翻转，这时需要三个变量进行操作，依次是pre(上一个节点)、cur(当前节点)、nxt(下一个节点)。原链表中，pre指向cur，cur指向nxt，我们需要做的是直接让pre指向空，让cur指向pre。如下图所示

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/

class Solution { //原地翻转
public:
    ListNode* ReverseList(ListNode* pHead) {
		if(pHead == nullptr) return nullptr;
		ListNode *pre, *cur, *nxt;
		pre = nullptr; //pre一开始为空
		cur = pHead; //cur指向第一个节点
		while(cur != nullptr) {
			nxt = cur->next; //保存下一个节点的地址
			cur->next = pre; //原地反转
			pre = cur; //后移，准备下一次反转
			cur = nxt;
		}
		return pre; //此时pre指向最后一个节点，而cur为空
    }
};


class Solution {//头插法
public:
    ListNode* ReverseList(ListNode* pHead) {
		ListNode *Head = new ListNode(0); //新建一个头节点
		ListNode *tmp; 
		while(pHead) {
			tmp = pHead->next;//保存下一个头节点地址
			pHead->next = Head->next;//头插法
			Head->next = pHead;
			pHead = tmp;
		}
		return Head->next;
    }
};

BM2 链表内指定区间反转

 题意：给你一个链表，让你在链表的指定区间进行反转

 题解：此题就是上一题的进阶版，对于第一题的两种方法接可用于此题。由于是对链表中间的某  一段区间进行操作，我们还要保证操作之后这一段与原链表要连接在一起。所以要保存这四个节点，翻转区间的首尾节点，以及原链表中与这段区间相连接的两个节点。以下给出头插法的代码。

class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        ListNode *pHead = new ListNode(0);//头节点
        ListNode *pre, *cur, *nxt, *tmp;//四个端点节点
        pHead->next = head;
        pre = pHead;
        cur = head;
        for(int i = 1; i <= n; ++i) {
            if(i < m) {//未到区间，向后遍历
                pre = pre->next;
                cur = cur->next;
            } else if (i >= m) {
                if(i == m) tmp = cur;//区间的第一个节点在翻转后会变成末尾节点，用tmp保存
                nxt = cur->next;//头插法
                cur->next = pre->next;
                pre->next = cur;
                cur = nxt;
            }
        }
        //翻转结束后，nxt会指向区间段的后一个节点
        //将区间与与原链表后面一段进行连接
        tmp->next = nxt;
        return pHead->next;
    }
};

BM3 链表中的节点每k个一组翻转

  题意：给你一个链表，每k个节点为一组进行翻转。

  题解：上一题的进阶版，思路大致一样，就是要注意一些细节。

class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        if(head == nullptr || k == 1) return head;
        ListNode *pHead = new ListNode(0);
        ListNode *pre, *nxt, *tmp, *cur, *p;
        int num = 0;
        pHead->next = head;
        pre = pHead;
        tmp = cur = p = head;
        while(p != nullptr) {//求链表长度
            p = p->next;
            num++;
        }
        if(head == nullptr || k == 1 || num < k) return head;
        for(int i = 1; i <= (num / k) * k; ++i) {//长度小于k的那一段无需进行翻转
            if(i % k == 1 && i != 1) {//进入下一段时，将翻转好的区间连接
                tmp->next = nxt;//进行连接
                pre = tmp;//更新pre
                tmp = cur;//更新tmp
            }
            nxt = cur->next;//头插法
            cur->next = pre->next;
            pre->next = cur;
            cur = nxt;
        }
        tmp->next = nxt;//连接剩下的一段
        return pHead->next;
    }
};

BM4 合并两个排序的链表

题意：给你两个有序的链表，让你合成为一个有序的链表。

题解：设置两个指针指向两个链表，依次对比大小，使用尾插法进行连接（就是连接在队尾），要注意的是当一个链表遍历完了之后，另一个链表大概率还剩下一截，要把剩下的链表连接。

class Solution {
public:
    ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
        ListNode *Head = new ListNode(0);//设置一个头结点方便操作
		ListNode *p1 = pHead1, *p2 = pHead2, *p = Head;
		while(p1 != nullptr && p2 != nullptr) {
			if(p1->val <= p2->val) {
				p->next = p1;
				p1 = p1->next;
			} else {
				p->next = p2;
				p2 = p2->next;
			}
			p = p->next;
		}
        //将剩下的节点接上
		if(p1 != nullptr) p->next = p1;
		if(p2 != nullptr) p->next = p2;
		return Head->next;
    }
};

BM5 合并k个已排序的链表

题意：给你n个有序的链表，让你合成为一个有序的链表。

题解：上一题的进阶版。上一题设置了两个指针进行比较，这里我们依旧可以采用这种思路，设置k个指针指向这k个链表。但是题目要求的时间复杂度是O(nlogn)，如果简单的让这k个指针进行比较，那每次选出一个最小值的结点的时间都需要O(k)的时间，选出n个节点的时间复杂度将会达到O(n*k)相当于O(n^2)。此时我们观察到，每次操作只需选出一个最小值节点，而将指向这个节点的指针往后移，相当于删除这个节点后新增一个节点，自然而然可以想到数据结构  堆。小根堆的每次插入和删除操作都是O(logn)的时间复杂度，意味着选出一个最小值节点的时间复杂度为O(logn),n个节点的时间复杂度为O(nlogn)，满足题目要求。优先队列的底层就是堆，将这k个指针丢入优先队列，按照上述的过程更新优先队列，即可合成一个有序的链表。

struct node {
    int val;//小根堆中每个节点的值
    ListNode *cur;//指针当前指向的位置

    //结构体重载运算符，不懂自行百度
    bool  operator < (const node &q) const {
        return val > q.val;
    }
};
priority_queue<node> que;//优先队列
class Solution {
public:
    ListNode *mergeKLists(vector<ListNode *> &lists) {
        for(int i = 0; i < lists.size(); ++i) {
            if(lists[i] != nullptr) {//将指针丢入优先队列
                que.push({lists[i]->val, lists[i]});
            }
        }
        ListNode *pHead = new ListNode(0), *p;
        p = pHead;
        while(!que.empty()) {
            node tmp = que.top();
            que.pop();//删除节点
            p->next = tmp.cur;//进行连接
            p = p->next;
            tmp.cur = tmp.cur->next;
            if(tmp.cur != nullptr) que.push({tmp.cur->val, tmp.cur});//更新节点
        }
        return pHead->next;
    }
};