问题描述
假设有一个能装入总体积为T的背包和n件体积分别为w1,w2,w2,……,wn的物品,能否从n件物品中挑选若干件恰好装满背包,即使w1+w2+……+wn=T,要求找出所有满足上述条件的解。例如:当T=10,各件物品的体积{1,8,4,3,5,2}时,可找到下列4组解:
(1,4,3,2)
(1,4,5)
(8,2)
(3,5,2)
解题思路
可利用回溯法的设计思想来解决背包问题。首先将物品排成一列,然后顺序选取物品装入背包,假设已选取了前i件物品之后背包还没有装满,则继续选取第i+1件物品,若该物品“太大”不能装入,则弃之而继续选取下一件,直至背包装满为止。但如果在剩余的物品中找不到合适的物品以填满背包,则说明“刚刚”装入背包的那件物品不合适,应将它取出弃之一边,继续再从它之后的物品中选取,如此重复,直至求得满足条件的解,或者无解。
代码
#include <iostream>
#include <malloc.h>
using namespace std;
/*
任务描述: 假设有一个能装入体积为T的背包和n件体积分别为w1,w2,…,wn的物品,能否从n件物品中挑选出
若干件恰好装满背包,即时w1 + w2 + …+ wn = T,
要求找出所有满足上述条件的解。例如:当T=10,各件物品的体积{1,8,4,3,5,2}时,
可找到下列4组解:
(1,4,3,2)、(1,4,5)、(8,2)、(3,5,2)。
作者:Mr.Lu
时间:2019-6-8
*/
//使用栈作为结构体
typedef struct {
int data[100];//
int top, first=0;
}stack;
//向栈中添加元素
int push(stack *s, int data){
s->data[s->top++] = data;
return data;
}
//从栈中删除元素
int pop(stack *s){
s->top--;
// cout<<s->top<<endl;
int data = s->data[s->top];
return data;
}
int main(){
double T, w[100];//假设最多有100种不同大小的物品
int n;
stack s;
int num = 0;//记录解的总数
double sum = 0;//记录栈中所有元素的值的和
cout<<"请输入背包的总体积:";
cin>>T;
cout<<"请输入物品种类数:";
cin>>n;
cout<<"请输入每种物品的体积:";
for(int i=0; i<n; i++){
cin>>w[i];
}
cout<<"满足条件的解有:"<<endl;
for(int i=0; i<n; i++){
//栈的初始化
s.top = 0;
sum = 0;
int r, p;//r记录是否循环到了底,p记录当前栈顶元素的位置
sum += w[push(&s, i)];
r = p = i+1;
if(sum > T){
continue;
}
else{
while(s.top!=0){
if(sum < T && r<n){
sum += w[push(&s, r)];
r++;
}
if(sum > T){
sum -= w[pop(&s)];
}
if(sum == T){
for(int k=s.first; k<s.top; k++){
cout<<w[s.data[k]]<<" ";
}
cout<<endl;
num++;
sum -= w[pop(&s)];
}
if(r == n){
p = pop(&s);
if(s.top==0){
break;
}
sum -= w[p];
p++;
if(p<n){
sum += w[push(&s, p)];
p++;
r = p;
}
else{
p = pop(&s);
if(s.top==0)
break;
sum -= w[p];
p++;
sum += w[push(&s, p)];
p++;
r = p;
}
}
}
}
}
if(num!=0){
cout<<"解的个数为:"<<num<<endl;
}
}
代码设计思路:首先使用栈来存储物品,在代码中已经定义了栈的结构体,整型变量top指向了栈的顶部元素,整型变量first指向了栈的底部(始终不变)。然后在下面,写了栈的相关操作,入栈与出栈,返回的都是当前栈顶元素的值(存入栈顶部的物品体积)。在主函数中,变量名的后面都做了相关的注释,可能大家看不懂的就是r,p三个整形变量的意义。p是记录当前栈顶元素在n件物品中的下一个位置,r是记录当前所要压入栈中的物品元素的位置。for循环中,每一次循环,都会进行一次初始化,然后将w[i]压入栈顶,进行回溯操作。对于T=10,各件物品的体积{1,8,4,3,5,2}时,for循环里面进行的操作可以用下列循环图表示。
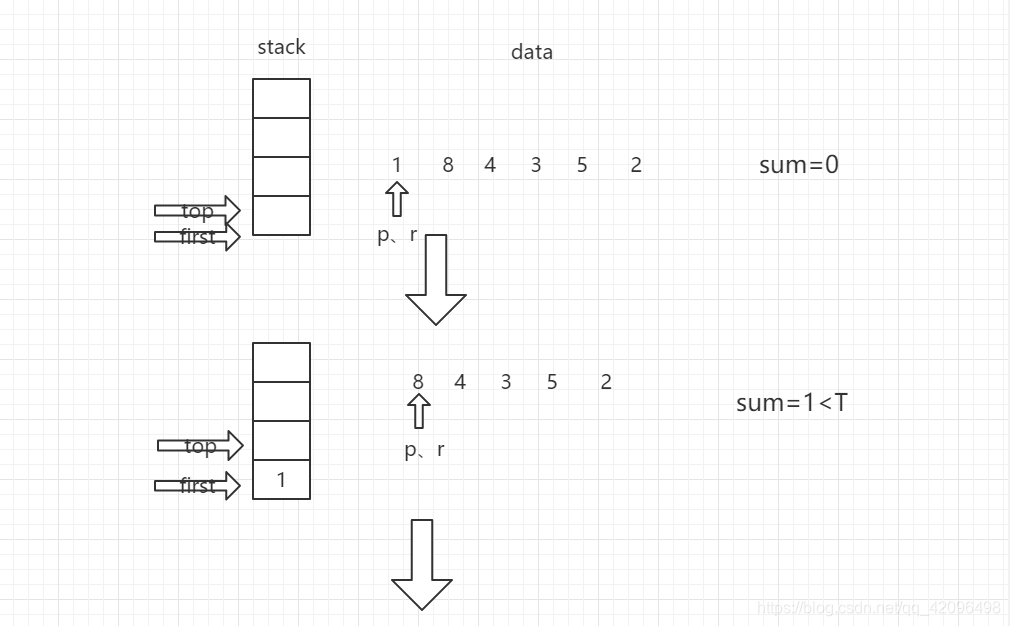
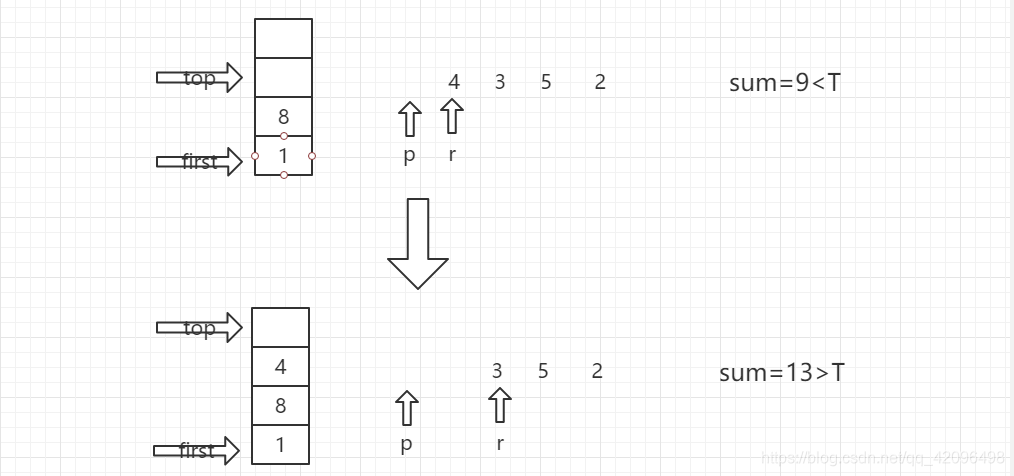
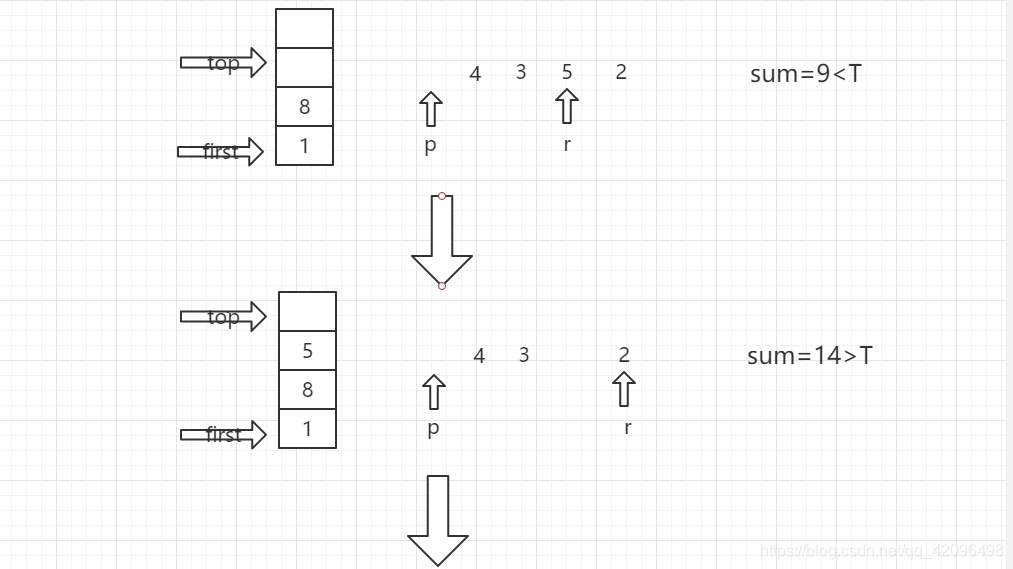
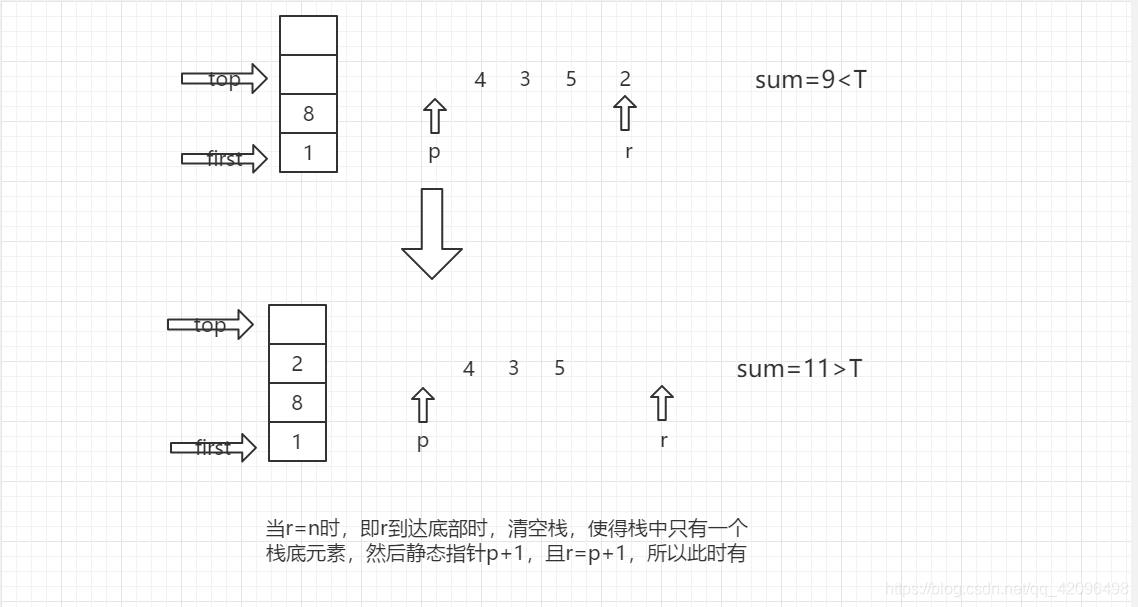
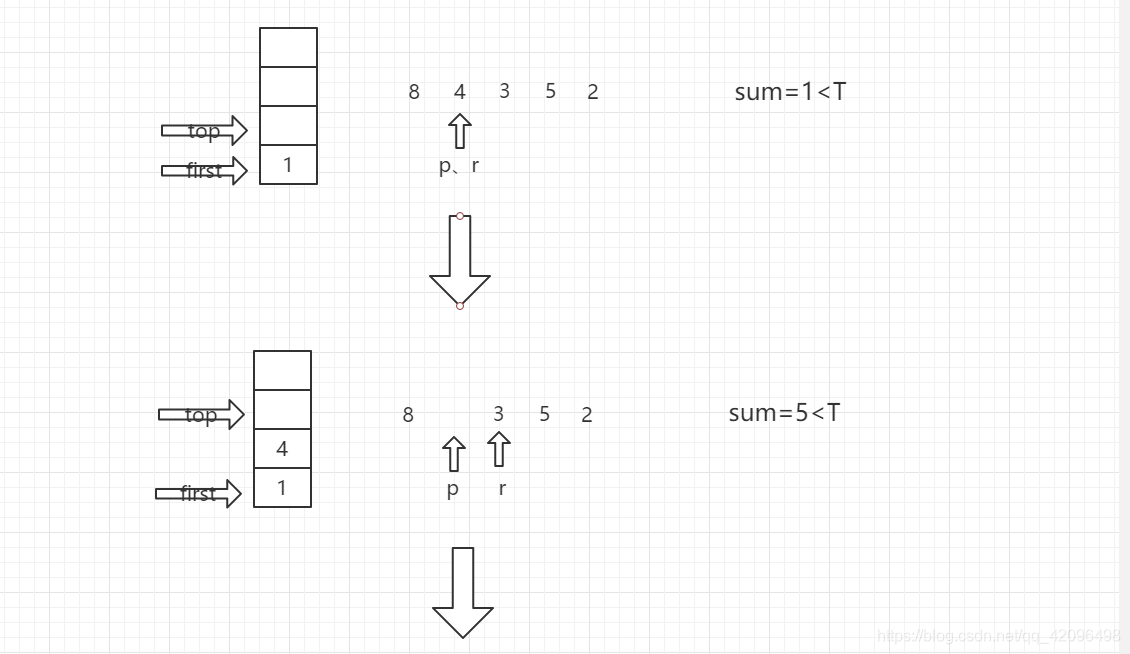

这样循环下去,如果sum=T,则从栈底first到栈顶top输出所有元素,如果sum<T,继续入栈,如果sum>T,出栈。当r=n时,使p+1,且让r=p,当p=n时,说明使元素1作为栈底元素已经把所有情况都遍历完。此时跳出循环,使之后的元素作为栈底元素,重复上述操作。
测试结果
1.背包体积T=10,各件物品的体积{1,8,4,3,5,2}
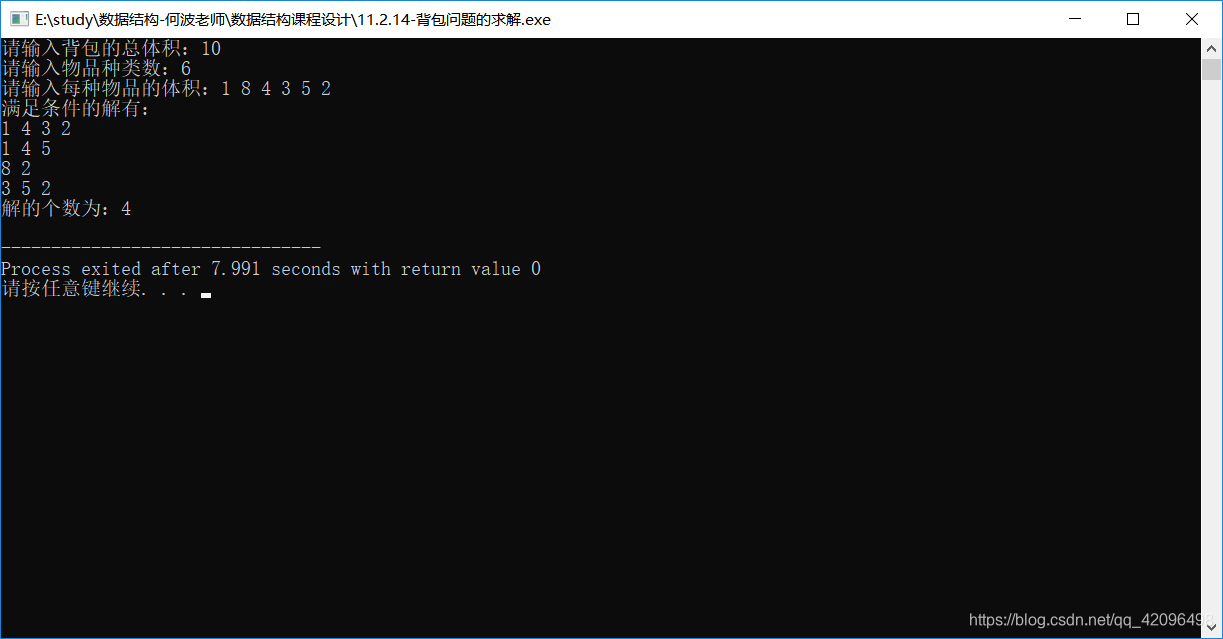
2.背包体积T=20,各件物品体积{5 ,8, 4, 3, 6, 9, 2, 1}
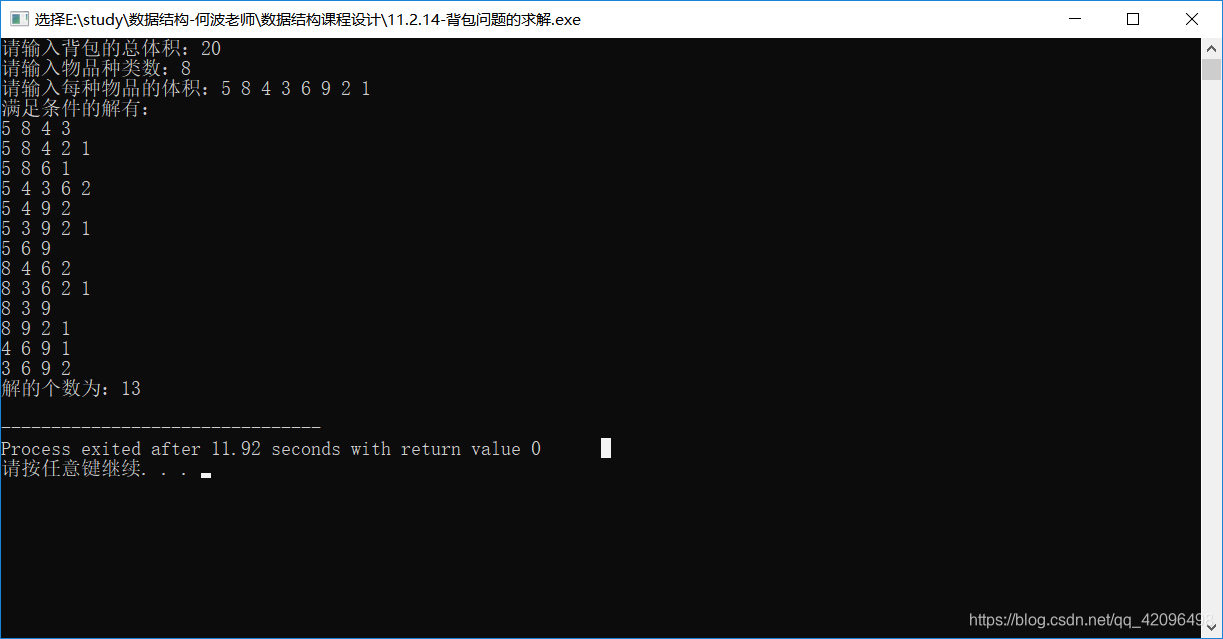








 博客围绕背包问题展开,即从n件物品中挑选若干件恰好装满总体积为T的背包。采用回溯法解题,先将物品排序,顺序选取装入,不合适则回溯。代码用栈存储物品,通过入栈、出栈操作遍历所有可能。还给出了不同背包体积和物品体积的测试结果。
博客围绕背包问题展开,即从n件物品中挑选若干件恰好装满总体积为T的背包。采用回溯法解题,先将物品排序,顺序选取装入,不合适则回溯。代码用栈存储物品,通过入栈、出栈操作遍历所有可能。还给出了不同背包体积和物品体积的测试结果。
















 5362
5362

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








