前面介绍了5种不同的分类算法,它们各有优缺点。我们可以将不同的分类组合起来,这种组合结果称为集成算法,或元算法。
优点:泛化错误率低,易编码,可以应用在大部分分类器之上,无参数调整。
缺点:对离群点敏感。
1.bagging:基于数据随机重抽样的分类器构建方法
自举汇聚法(bootstrap aggregating),也称bagging方法。是从原始数据集选择S次后得到S个新数据集的一种技术。
AdaBoost是adapptive boosting(自适应boosting)的缩写。AdaBoost为每个分类器都分配了一个权重值alpha,这些alpha值是基于每个弱分类器的错误率进行计算的。
2.Bagging、Boosting二者之间的区别
样本选择上:
- Bagging:训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。
- Boosting:每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。
样例权重:
- Bagging:使用均匀取样,每个样例的权重相等。
- Boosting:根据错误率不断调整样例的权值,错误率越大则权重越大。
预测函数:
- Bagging:所有预测函数的权重相等。
- Boosting:每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重。
并行计算:
- Bagging:各个预测函数可以并行生成。
- Boosting:各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果。
3.AdaBoost
(1)计算样本权重
训练数据中的每个样本,赋予其权重,即样本权重,用向量D表示,这些权重都初始化成相等值。假设有n个样本的训练集:

设定每个样本的权重都是相等的,即1/n。
(2)计算错误率

(3)计算弱学习算法权重
弱学习算法也有一个权重,用向量α表示,利用错误率计算权重α:

(4)更新样本权重
在第一次学习完成后,需要重新调整样本的权重,以使得在第一分类中被错分的样本的权重。

其中,  表示对第i个样本训练正确,不等于则表示分类错误。
表示对第i个样本训练正确,不等于则表示分类错误。  是一个归一化因子:
是一个归一化因子:
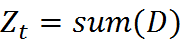
这个公式我们可以继续化简,将两个公式进行合并,化简如下:
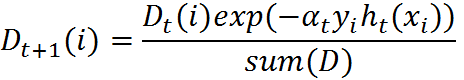
(5)AdaBoost算法
重复进行学习,这样经过t轮的学习后,就会得到t个弱学习算法、权重、弱分类器的输出以及最终的AdaBoost算法的输出。
四.基于单层决策树构建弱分类器
弱分类器使用单层决策树(decision stump),也称决策树桩,它是一种简单的决策树,通过给定的阈值,进行分类。
1.数据可视化
2.构建单层决策树
from numpy import *
def loadSimpData():
dataMat = matrix([[1,2.1],[2,1.1],[1.3,1.0],[1.0,1.0],[2.0,1.0]])
classLabels = [1.0,1.0,-1.0,-1.0,1.0]
return dataMat,classLabels
#单层决策树生成函数
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):
'''
dataMatrix - 数据矩阵
dimen - 第dimen列,也就是第几个特征
threshVal - 阈值
threshIneq - 标志
Returns:
retArray - 分类结果
'''
retArray = ones((shape(dataMatrix)[0],1)) #初始化retArray为1
if threshIneq == 'lt':
retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 #如果小于阈值,则为-1
else:
retArray[dataMatrix[:,dimen] > threshVal] = -1.0 #如果大于阈值,则为-1
return retArray
#找到数据集上最佳的单层决策树
def buildStump(dataArr,classLabels,D): # D:样本权重
dataMatrix = mat(dataArr)
labelMat = mat(classLabels).T
m,n = shape(dataMatrix)
numSteps =10; bestStump ={}; bestClassEst = mat(zeros((m,1))) #bestStump -最佳单层决策树信息
minError = inf #最小误差初始化为正无穷大
for i in range(n): #遍历所有特征
rangeMin = dataMatrix[:,i].min() #找到特征中最小值和最大值
rangeMax = dataMatrix[:,i].max()
stepSize = (rangeMax - rangeMin)/numSteps #计算步长
for j in range(-1,int(numSteps)+1):
for inequal in ['lt','gt']: #大于和小于的情况,均遍历。lt:less than,gt:greater than
threshVal = (rangeMin + float(j)*stepSize) #计算阈值
predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#计算分类结果
errArr = mat(ones((m,1))) #初始化误差矩阵
errArr[predictedVals == labelMat] =0 #分类正确的,赋值为0
print('errArr:',errArr)
weightedError = D.T *errArr #计算误差
print("split:dim %d,thresh %.2f,thresh inequal:%s,the weighted\
error is %.3f" %(i,threshVal,inequal,weightedError))
if(weightedError < minError): #找到误差最小的分类方式
minError = weightedError
bestClassEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump,minError,bestClassEst
算法运行结果:


五、使用AdaBoost提升分类器性能
在源代码基础上添加如下代码:
#基于单层决策树的AdaBoost训练过程
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
weakClassArr = [] #弱分类器相关信息列表
m = shape(dataArr)[0]
D = mat(ones((m,1))/m) #初始化权重向量的每一项值相等
aggClassEst = mat(zeros((m,1))) #累计估计值向量
for i in range(numIt):
bestStump,error,classEst = buildStump(dataArr,classLabels,D)
print('D:',D.T)
alpha = float(0.5*log((1-error)/max(error,1e-16))) #求单层决策树系数alpha
bestStump['alpha'] = alpha
weakClassArr.append(bestStump) #将该决策树存入列表中
print('classEst:',classEst.T) #打印决策树预测结果
expon = multiply(-1*alpha*mat(classLabels).T,classEst)
D = multiply(D,exp(expon)) #更新权重向量
D = D/D.sum()
aggClassEst += alpha*classEst #累加当前单层决策树的加权预测值
print('aggClassEst:',aggClassEst.T)
#求出分类错的样本个数
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))
errorRate = aggErrors.sum()/m
print('total error:',errorRate)
if errorRate == 0:
break
return weakClassArr #返回弱分类器的组合列表
结果如下图所示:

最后训练结果包含了三个弱分类器,其中包含了分类所需要的所有信息。一共迭代了3次,所以训练了3个弱分类器构成一个使用AdaBoost算法优化过的分类器,分类器的错误率为0。

测试算法:
#测试算法 AdaBoost分类函数
def adaClassify(datToClass,classifierArr): #@datToClass:测试数据点 @classifierArr:构建好的最终分类器
dataMatrix = mat(datToClass)
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m,1))) #初始化最终分类器
for i in range(len(classifierArr)): #遍历分类器列表中的每一个弱分类器
#每一个弱分类器对测试数据进行预测分类
classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\
classifierArr[i]['thresh'],classifierArr[i]['ineq'])
aggClassEst += classifierArr[i]['alpha']*classEst #加权累加
print(aggClassEst)
return sign(aggClassEst)

六、在一个数据集上应用AdaBoost
首先要有向文件中加载数据的方法,即loadDataSet()方法。
#自适应数据加载函数
def loadDataSet(fileName):
numFeat = len(open(fileName).readline().split('\t'))
dataMat = [] ; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat-1):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
绘制ROC曲线:
#ROC曲线的绘制及AUC计算函数
def plotROC(predStrengths,classLabels):
import matplotlib.pyplot as plt
cur = (1.0,1.0) #绘制光标的位置
ySum = 0 #用于计算AUC
numPosClas = sum(array(classLabels) ==1) #统计正例的数量
yStep = 1/float(numPosClas) #y轴步长
xStep = 1/float(len(classLabels)-numPosClas) #x轴步长
sortedIndicies = predStrengths.argsort() #预测强度排序
print("sored:",sortedIndicies)
fig = plt.figure()
fig.clf()
ax = plt.subplot(111) #表示图在1行1列的第一个位置
for index in sortedIndicies.tolist()[0]: #tolist转化为列表,[0]是矩阵在转为列表的注意事项
if classLabels[index] ==1.0:
delX = 0; delY = yStep;
else:
delX = xStep; delY = 0;
ySum += cur[1] #高度累加
ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b') #绘制ROC
cur = (cur[0]-delX,cur[1]-delY) #跟新绘制光标的位置
ax.plot([0,1],[0,1], 'b--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC curve for AdaBoost Horse Colic Detection System')
ax.axis([0,1,0,1])
plt.show()
print('the Area Under the Curve is:',ySum*xStep)
测试结果:

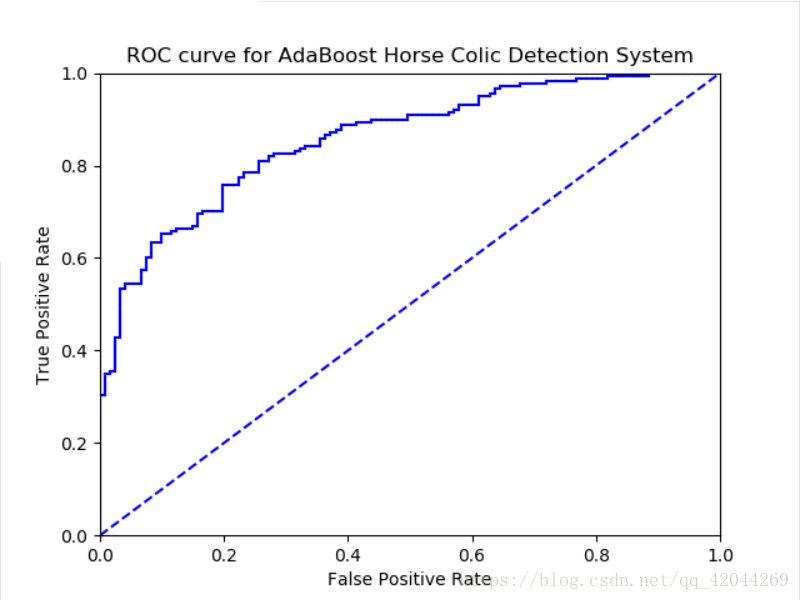




 博客介绍了集成算法,重点讲解了Bagging和AdaBoost。Bagging是基于数据随机重抽样构建分类器,AdaBoost为分类器分配基于错误率计算的权重。还对比了Bagging和Boosting在样本选择、样例权重等方面的区别,阐述了AdaBoost计算步骤,以及基于单层决策树构建弱分类器、提升分类器性能和应用实例。
博客介绍了集成算法,重点讲解了Bagging和AdaBoost。Bagging是基于数据随机重抽样构建分类器,AdaBoost为分类器分配基于错误率计算的权重。还对比了Bagging和Boosting在样本选择、样例权重等方面的区别,阐述了AdaBoost计算步骤,以及基于单层决策树构建弱分类器、提升分类器性能和应用实例。
















 267
267

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








