蒙特卡洛圆周率计算

最新推荐文章于 2025-07-03 23:49:07 发布
最新推荐文章于 2025-07-03 23:49:07 发布
阅读量3.9k 收藏 8
点赞数 1
CC 4.0 BY-SA版权
分类专栏： Python 文章标签： python 圆周率计算
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_42020563/article/details/80657239
本文介绍了Python标准库random用于生成随机数的功能，包括基本和扩展的随机数函数。重点讨论了使用蒙特卡洛方法计算圆周率的实例，通过这种方法在0.92642秒内估算出圆周率值，展示了计算思维在解决数学问题中的应用。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

random库是使用随机数的python标准库。

伪随机数：采用梅森旋转算法生产的伪随机数列中元素

random库主要用于生成随机数


基本随机数函数

随机数种子



相同的种子生成的随机数是相同的，可以复现结果。

扩展随机数函数




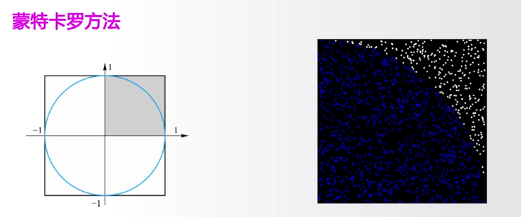
例 圆周率的计算

蒙特卡洛方法


from random import rand
最低0.47元/天 解锁文章

200万优质内容无限畅学
Day9：蒙特卡洛法（求圆周率）
黄粱一梦
07-09 3880
Day9：蒙特卡洛法（求圆周率） 一. 问题背景： 在只有一个随机数生成器的情况下如何估计π的大小？ 二. 解决思路： 蒙特卡洛法： 蒙特卡洛方法又称统计模拟法，随机抽样技术，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法。是使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近...
计算圆周率——蒙特卡洛法
那就平安囍樂的博客
09-21 1224
统计圆内的点数c，c与n的比值乘以4，就是π的值。编程实现用蒙特卡洛方法计算π值，为了自动测评的需要，请先读入一个正整数sd作为随机数种子，并要求使用 x,y = random.uniform(-1,1) , random.uniform(-1,1) 语句来生成随机点的坐标值。用蒙特卡洛方法计算圆周率π的原理如下：一个边长为2r的正方形内部相切一个半径为r的圆，圆的面积是πr2，正方形的面积为4r2，二者面积之比是π/4，因为比值与r大小无关，所以可以假设半径 r的值为1。
蒙特卡洛方法计算圆周率-.
06-17
蒙特卡洛方法计算圆周率 论文格式
蒙特卡洛法计算圆周率
wbk0127的博客
04-07 4249
一般情况下，针对得到的样本数据集创建相对模糊的模型，通过蒙特卡罗方法对于模型中的参数进行选取，使之于原始数据的残差尽可能的小，从而达到创建模型拟合样本的目的。2、首先根据题目要求，生成伪随机数， 设置随机数种子random.seed(123)，接着获取用户输入的撒点数量，同时定义计数器，记录圆内点的数量。借助random函数可以生成大量均匀分布的坐标点，接着统计出图形内的点数，通过它们占总点数的比例和坐标点生成范围的面积就可以求出的近似值。大数定律是描述相当多次数重复试验的结果的定律，在大数定理的保证下，
蒙特卡洛方法：随机抽样的艺术与科学
最新发布
拒绝AI玄学，只聊真技术▲
07-03 1038
— 它让不可解的问题变得可计算，让复杂的分布变得可采样。
蒙特卡洛算法（Monte Carlo algorithm）求圆周率
星空_MAX
05-15 4504
蒙特卡洛算法是统计模拟算法的一种，蒙特卡洛算法的数学理论基础是大数定理，在事件发生次数多的情况下，利用事件发生的频率作为时间发生概率的近似值 统计问题可直接求解，对于连续问题可不用离散化 与穷举法相对比而言，属于随机搜索，而穷举法属于给定特定规则的搜索 下面给出一个实例，来让蒙特卡洛算法求出圆周率 在一个2*2的矩形内，随机生成点，求在圆中相对矩形的数量比例，从而推出圆周率 推导过程： 矩形面积：圆的面积 = 所有点的数量：落在圆中点的数量 => 4r*r ：Pi*r*r =所有点.
蒙特卡洛法计算圆周率π（Python，Java，c 三种方式详解）
热门推荐
她的坏机器人
01-30 4万+
一、蒙特卡洛法简介 蒙特·卡罗方法（MonteCarlomethod），也称统计模拟方法，一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。 二、蒙特卡洛法计算圆周率的原理 正方形的面积为： 圆的面积为： 圆的面积比上正方形的面积为：π / 4 所以我们使用蒙特卡洛法在正方形内随机撒点，落在圆内的点 / 落在正方形内...
蒙特卡洛方法计算圆周率的数值
03-26
使用蒙特卡洛方法计算圆周率的数值
Monte_Carlo_1.zip_圆周率_圆周率计算_蒙特卡洛 积分_蒙特卡洛积分_计算圆周率
09-14
利用蒙特卡洛方法计算圆周率的基本思想是：假设有一个边长为2的正方形，其中包含一个半径为1的单位圆。如果我们随机在这个正方形内生成大量点，那么这些点落在圆内的概率就是π/4。通过统计落入圆内的点的数量，并与...
蒙特卡洛方法计算圆周率.py
07-27
初学python，以概率的方法——蒙特卡洛方法求圆周率，以此练手
蒙特卡洛算法求圆周率
qq_44783220的博客
08-10 696
#include "iostream" #include <time.h> #define MAX_ITERS 1000000 using namespace std; double Rand(double L, double R) { return L + (R - L) * rand() * 1.0 / RAND_MAX; } double GetPi() ...
Java 蒙特卡洛算法求圆周率近似值实例详解
08-29
主要介绍了蒙特卡洛算法的起源，特点，以及Java编程中利用蒙特卡洛算法计算圆周率近似值的实例,需要的朋友可以参考下
random库与使用蒙特卡洛方法计算圆周率
weixin_41442912的博客
05-30 1900
简介random库Python的另一个标准库，它主要是用来生成随机数的。random库生成的随机数是采用梅森旋转算法生成的（伪）随机数。主要的函数常用函数random.seed(a=None)初始化一个随机数的种子，默认为系统的时间。相同的种子对应的随机数是相同的。random.random()随机生成（0.0，1.0）之间的小数。这个函数在随机数使用中比较常用。通过一个实例...
Python：蒙特卡洛方法求圆周率
YO__Y的博客
06-13 1633
使用蒙特卡洛方法求圆周率。基本思想：利用圆与其外接正方形面积之比为 pi ／的关系，通过产生大量均匀分布的二维点，计算落在单位圆和单位正方形的数量之比再乘以4便得到 pi 的近似值。样本点越多，计算出的数据将会 近真识的 pi .
蒙特卡洛模拟（求圆周率）
亦是远方的小地方
08-29 3595
蒙特卡洛模拟；仿真；MatLab；数学建模；求圆周率；
蒙特卡洛方法求圆周率
06-07 1760
用随机优化算法--蒙特卡洛算法求圆周率 $\pi$
蒙特卡洛方法计算圆周率
李祖平大人的博客
02-24 2223
C语言实现蒙特卡洛方法计算圆周率
小木大数据-蒙特卡洛法求圆周率
小木的博客
06-21 911
我们配置好了spark和zk，下一步就是启动它们了，启动的方法是先把slave2,5,6的zk首先启动起来，然后到master这台机器上启动spark，最后到slave1上面启动备用的Spark-Master节点，从而实现高可用架构。接下来我来说一下什么叫做蒙特卡洛法，很简单，我们现在有一个变长为2的正方形，里面内嵌一个半径为1的圆： 我们把这个东西分为三部分，一部分是圆的内部，一部分是圆的外部且...
Python:利用蒙特卡洛方法求解圆周率
u011732210的博客
12-18 1731
【代码】Python:利用蒙特卡洛方法求解圆周率。
蒙特卡洛计算圆周率
04-02
<think>好的，我现在需要帮助用户了解如何使用蒙特卡洛方法计算圆周率。首先，我得回顾一下蒙特卡洛方法的基本原理，确保自己理解正确。蒙特卡洛方法是一种通过随机采样和概率统计来求解数值问题的技术，对吧？比如通过生成大量随机点，然后统计落在特定区域的点的比例来估计面积或积分。 用户的问题是关于计算圆周率π的，所以我需要将这个方法应用到圆的面积估算上。我记得圆的面积公式是πr²，而正方形的面积是边长的平方。假设我们取一个边长为2的正方形，内切一个半径为1的圆。这样，圆的面积就是π，正方形的面积是4。两者的面积比就是π/4，这个比例应该等于在正方形内随机生成的点落在圆内的概率。 接下来，步骤应该是这样的：生成大量的随机点（比如N个），然后计算有多少点落在圆内（记为M个）。然后π≈4*M/N。这个公式对吗？是的，因为M/N近似于π/4，乘以4就得到π的估计值。 现在需要考虑如何具体实现这个过程。比如，在编程中，如何生成均匀分布在正方形内的点？通常使用随机数生成器，范围在[-1,1]之间，这样正方形的中心在原点，边长为2。对于每个点(x,y)，计算x² + y²是否小于等于1，如果是，就算落在圆内。 然后，用户可能需要示例代码。Python是一个常用的语言，所以用Python写个简单的例子比较合适。代码的大致结构是循环生成N次随机点，统计符合条件的情况，最后计算4*M/N。同时，可能需要考虑如何提高精度，比如增加N的值，或者多次运行取平均。 但是用户提供的引用中有提到近似计算圆周率的例子，比如引用3提到在编程课中引入这个实验。所以可能需要结合这些引用内容，确保回答符合已有的资料。例如，引用1提到蒙特卡洛方法得出的值接近理论值，说明方法的有效性；引用2讨论的是用蒙特卡洛模拟硬币抛掷，这和生成随机点类似，都是通过大量实验逼近理论概率。 另外，用户的问题可能需要分步骤解释，确保结构清晰。比如，先讲原理，再讲步骤，然后给代码示例，最后讨论影响精度的因素。同时，按照用户的系统指令，数学表达式需要用$...$，独立公式用$$...$$，并且正确使用LaTeX语法。 可能的疑问点包括：为什么正方形的边长是2？其实边长也可以是其他值，但为了方便计算，选择边长为2且中心在原点，这样坐标范围是[-1,1]，计算距离更方便。另外，如何验证这个方法的正确性？比如当N趋近于无穷大时，估计值是否趋近于π。 然后，需要考虑生成的相关问题。根据示例，可能需要提出关于蒙特卡洛方法的其他应用、如何提高计算精度、或与其他方法比较的问题。例如，蒙特卡洛方法的误差分析，或者如何在编程中优化这个过程。 最后，检查是否需要引用提供的资料。引用1和引用3都提到了蒙特卡洛方法的应用，可以在回答中适当引用，比如在说明方法有效性时提到引用1的结果。引用2虽然讲的是硬币抛掷，但可以类比到生成随机点的随机性，不过可能不需要直接引用。 现在，确保回答结构符合用户的要求：使用中文，分步骤说明，代码用正确格式，数学表达式正确，生成相关问题，并在引用处添加标识。例如，在提到蒙特卡洛方法接近理论值时，引用[^1]。</think>### 使用蒙特卡洛方法计算圆周率的步骤 #### 1. **基本原理** 蒙特卡洛方法通过随机采样和概率统计估算数值。对于圆周率$π$的计算，可在一个边长为$2$的正方形内生成均匀分布的随机点，并统计落在其内切圆（半径$1$）中的点的比例。圆与正方形的面积比为$π/4$，因此可通过比例估算$π$[^1]。 #### 2. **数学推导** - 正方形面积：$S_{\text{正方形}} = (2r)^2 = 4$（设半径$r=1$）。 - 圆面积：$S_{\text{圆}} = πr^2 = π$。 - 随机点落在圆内的概率：$P = S_{\text{圆}} / S_{\text{正方形}} = π/4$。 - 若生成$N$个点，其中$M$个在圆内，则$π ≈ 4M/N$。 #### 3. **算法实现** ```python import random def estimate_pi(n_samples): count_inside = 0 for _ in range(n_samples): x = random.uniform(-1, 1) # 生成[-1,1)的随机坐标 y = random.uniform(-1, 1) if x**2 + y**2 <= 1: # 判断是否在圆内 count_inside += 1 return 4 * count_inside / n_samples # 示例：使用100万样本估算π print(estimate_pi(1_000_000)) # 输出可能接近3.1415 ``` #### 4. **精度与误差分析** - 精度取决于样本量$N$，误差通常以$O(1/\sqrt{N})$的速度下降[^1]。 - 例如，$N=10^6$时误差约为$0.001$，与引用[1]中提到的$0.886$（可能涉及不同应用）的误差趋势一致。 #### 5. **优化方向** - **增加样本量**：直接提高计算精度，但计算成本增加。 - **并行计算**：利用多线程/分布式加速采样。 - **方差缩减技术**：如重要性采样（需结合具体场景）。 ---
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值