LFSR(线性反馈移位寄存器)

最新推荐文章于 2025-07-09 23:17:37 发布

原创最新推荐文章于 2025-07-09 23:17:37 发布 · 2.7w 阅读

36 ·

CC 4.0 BY-SA版权

文章标签：

#Verilog

嵌入式学习专栏收录该内容

47 篇文章

订阅专栏

本文详细介绍了线性反馈移位寄存器(LFSR)的工作原理及其在计数器设计中的应用。LFSR是一种特殊的移位寄存器，其下一个状态由当前状态的线性组合决定，常见于生成M序列。文章还探讨了LFSR的周期特性，抽头选择的重要性，以及如何通过特定的回授多项式实现最大长度的序列。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

线性反馈移位寄存器是指给定前一状态的输出，将该输出的线性函数再用作输入的移位寄存器。异或运算是最常见的但比特线性函数，对寄存器的某些位进行异或操作后作为输入，再对寄存器中各比特位进行整体移位。

module cy4(q3,clk,pre_n);
input clk,pre_n;
output reg q3;
reg q2,q1;

always @(posedge clk or negedge pre_n)
if(!pre_n) {q3,q2,q1} <= 3'b111;
else {q3,q2,q1} <= {q2,(q1^q3),q3};
endmodule

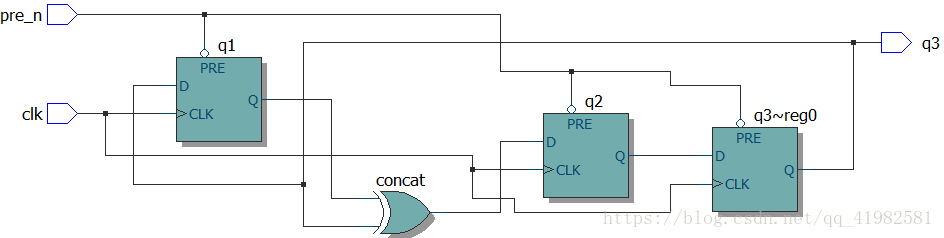
在这里插入图片描述

与常见的计数器相比，LFSR计数器具有速度快、消耗逻辑门少的特点。通常有n个触发器，其周期数为2^n-1个。
影响下一个状态的比特位叫做抽头。
最大长度的LFSR生成一个M序列（例如，只有与有一定抽序列的LFSR才能通过所有 2^n − 1 个内部状态，不包括全零状态），除非它本身为全零，亦即状态永不改。
多项式中常数**“1”**并不代表某一个抽头，它所指的是一个比特位的输入（例如等效为 1 ）。多项式中的指数代表从左至右的抽头位，第一个和最后一个比特一般相应的是输入和输出位。当且仅当相应的回授多项式是本原多项式时，LFSR才能达到最大长度。这表示以下条件是必须的：
抽头的数量必须为偶数。
抽头之间不能成对出现，必须是互质的。