【Leetcode 1039】多边形三角剖分的最低得分

最新推荐文章于 2023-04-02 15:46:27 发布

原创最新推荐文章于 2023-04-02 15:46:27 发布 · 238 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #数据结构 #算法 #cpp #leetcode

Algorithms 专栏收录该内容

20 篇文章

订阅专栏

本文探讨了如何给定一个凸N边多边形，将其剖分为N-2个三角形，并通过动态规划算法求解这些三角形顶点乘积之和的最低分。介绍了算法的实现细节及测试用例。

问题描述

给定 N，想象一个凸 N 边多边形，其顶点按顺时针顺序依次标记为 A[0], A[i], ..., A[N-1]。

假设您将多边形剖分为 N-2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 N-2 个三角形的值之和。

返回多边形进行三角剖分后可以得到的最低分。

测试用例1：

输入：[1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

测试用例2：
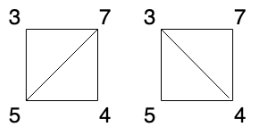
在这里插入图片描述
测试用例3：

输入：[1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

提示：

3 <= A.length <= 50
1 <= A[i] <= 100

参考实现：

class Solution {
public:
    int minScoreTriangulation(vector<int>& A) {
        int n = A.size();
        if(n==0)    return 0;
        vector<vector<int>> dp(n, vector<int>(n, INT_MAX));

        for(int i=0; i<n-1; ++i)
            dp[i][i+1] = 0;
        
        for(int length = 3; length <= n; ++length){
            for(int i = 0; i <= n - length; ++i){
                int j = i + length - 1;
                for(int k=i+1; k<=j-1; ++k)
                    dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + A[i] * A[j] * A[k]);
            }
        }
        return dp[0][n-1];
    }
};