本文详细介绍了在研究日常动作识别中，如何对EEG和sEMG数据进行采集、显示及预处理。通过对不同动作的sEMG信号进行傅里叶变换和小波去噪方法（WTD、WDFTD、IWD）的对比，发现组合小波去噪法在去除基线漂移和高频噪声方面表现最佳。同时，对EEG数据使用FIR滤波器进行带通滤波，以提取特定频率范围内的信号。预处理步骤对于提高动作识别的准确性和信噪比至关重要。
1、EEG数据与SEMG数据的采集与显示
1.1 SEMG数据显示
在该论文中所针对的动作是日常生活中喝水拿杯子动作的研究，并且将喝水这个动作分解为5个子动作，分别是Act1~Act5。除此以外再加上静息动作Act0。
使用肌电采集器将各个动作进行采集并保存数据，数据目录截图如下。其中1-5分别为5个子动作，6中存放的是静息动作
除了6静息动作以外，每组动作都采集了50次左右，用于后面进行数据的训练与测试，如下图所示
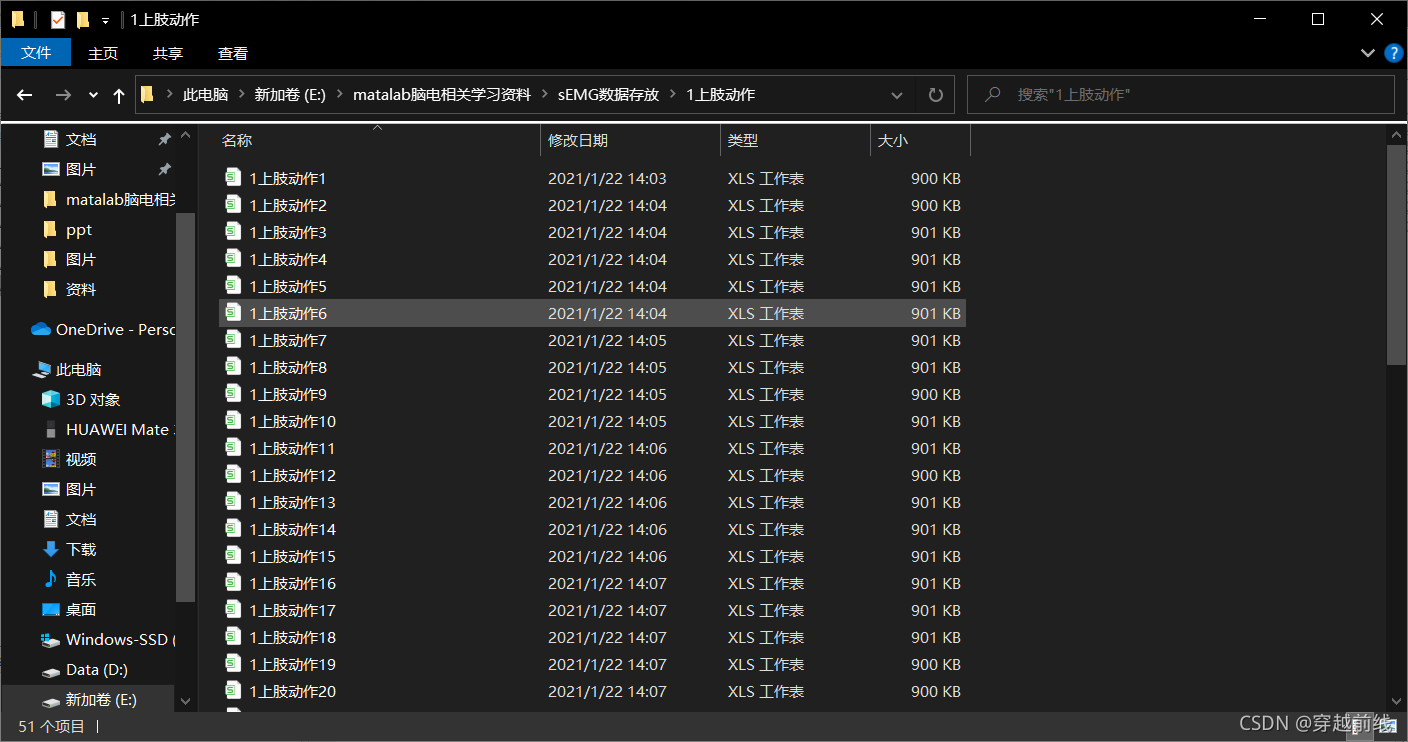
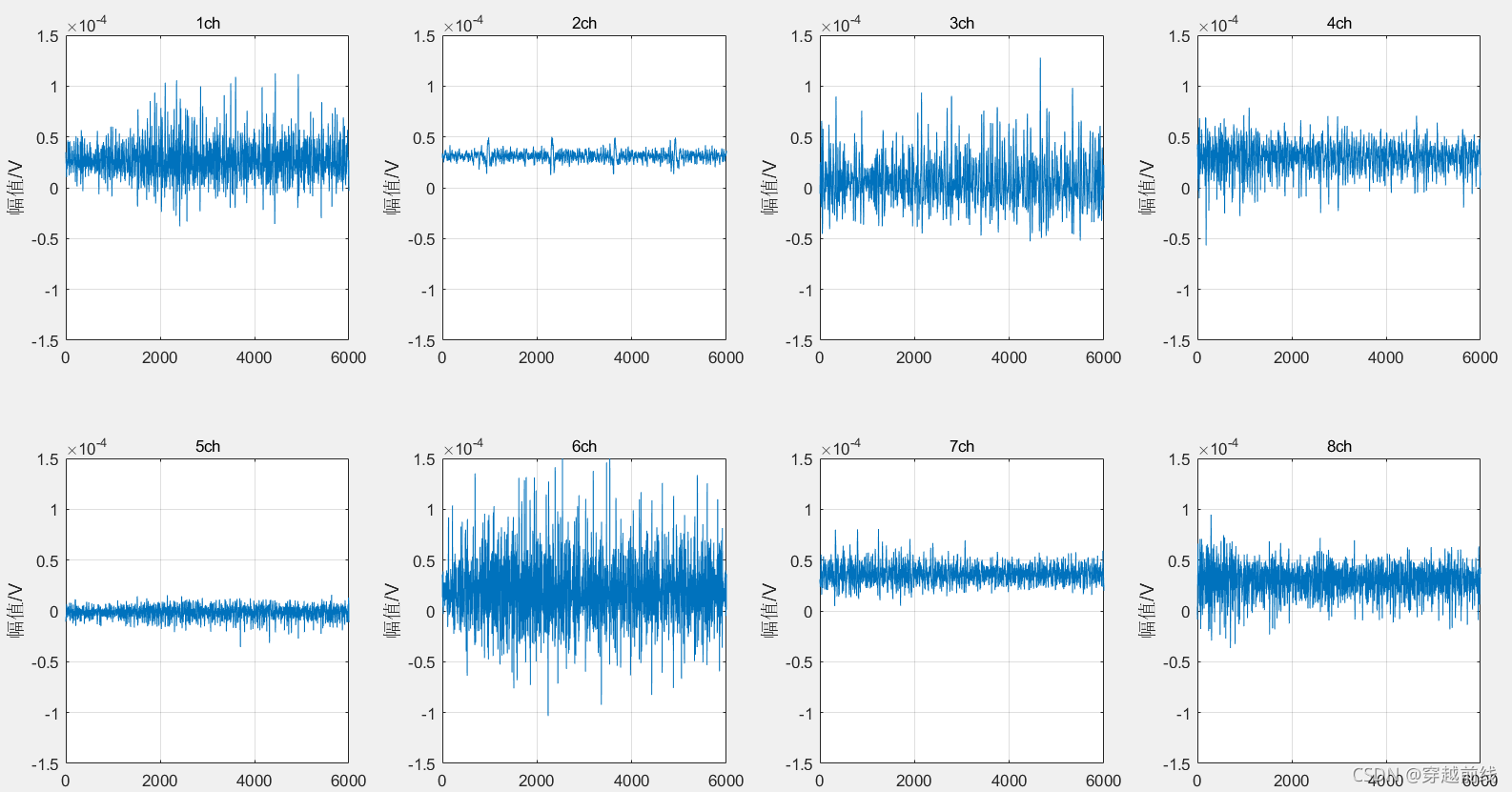
在此处通过matlab代码将6个动作的原始时域图显示出来。代码如下所示。（因为6个代码只有filename文件名不一样，所以在这里只展示一组代码，其余都是同理）
clear;
clc;
filename='/matlab.2019a/bin/paper review/sEMG数据存放/1上肢动作/1上肢动作24.csv'
P=csvread(filename);%从第1行第0列开始读取数据
figure(1);%creat figure window
for column_i = 1:8
sEMG=P(:,column_i);%获取一个通道的肌电数据
sEMG_1=length(sEMG);%获取一个通道的数据量
n = 0:sEMG_1-1;%横坐标数值
subplot(2, 4, column_i);
plot(n,sEMG);
grid;%显示或隐藏轴网格线，切换主栅格的可见性
ylabel('幅值/V','FontSize',12);%y轴的标签
title(sprintf('%dch',column_i),'FontSize',10);
axis([0 sEMG_1 -1.5*10^(-4) 1.5*10^(-4)])
end
做一下额外说明，上面代码中的上肢动作24，是随便取得一组数据，因为每个动作都采集了很多次，所以展示图片的时候，任意选择一组就行。
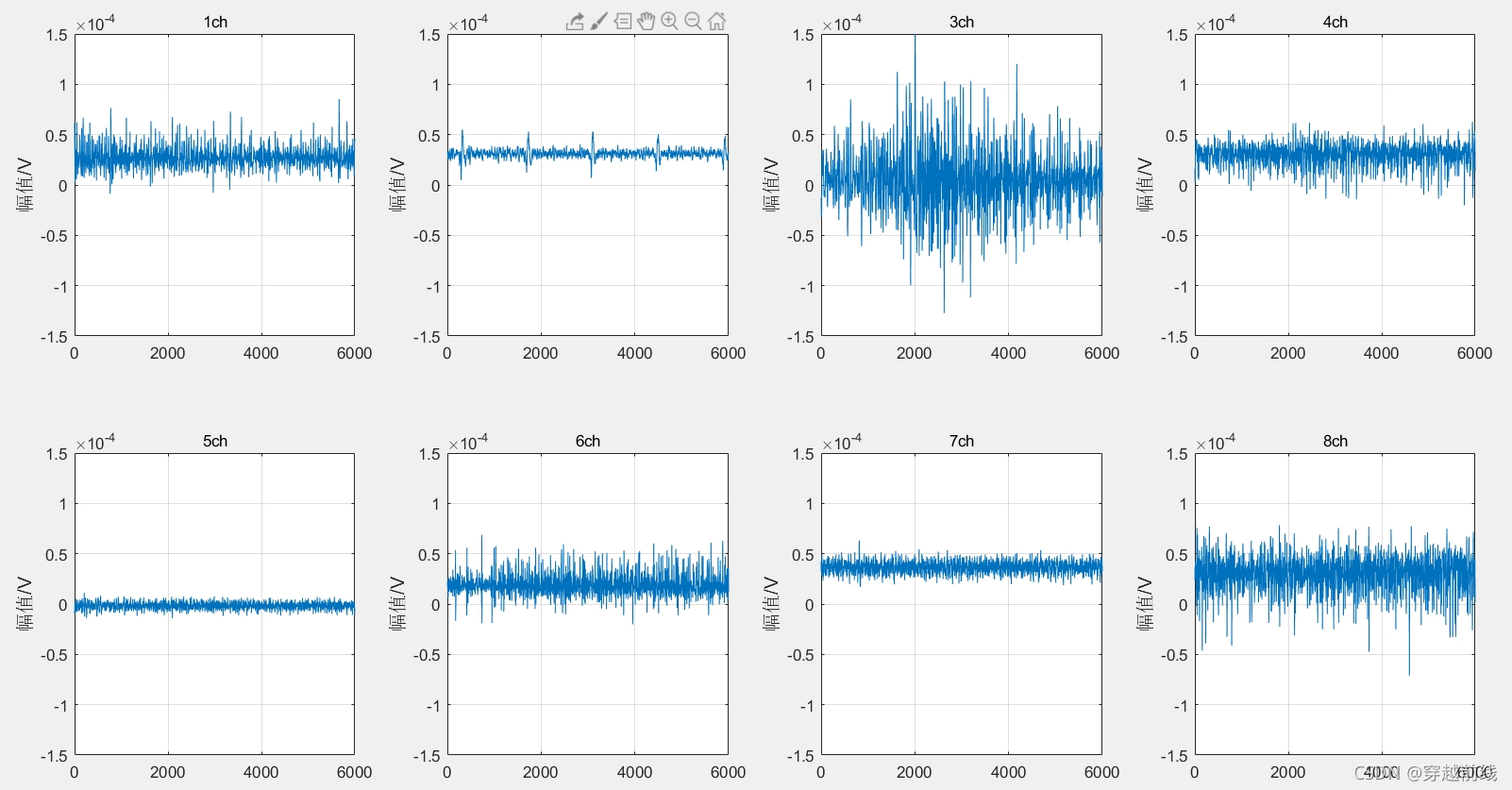
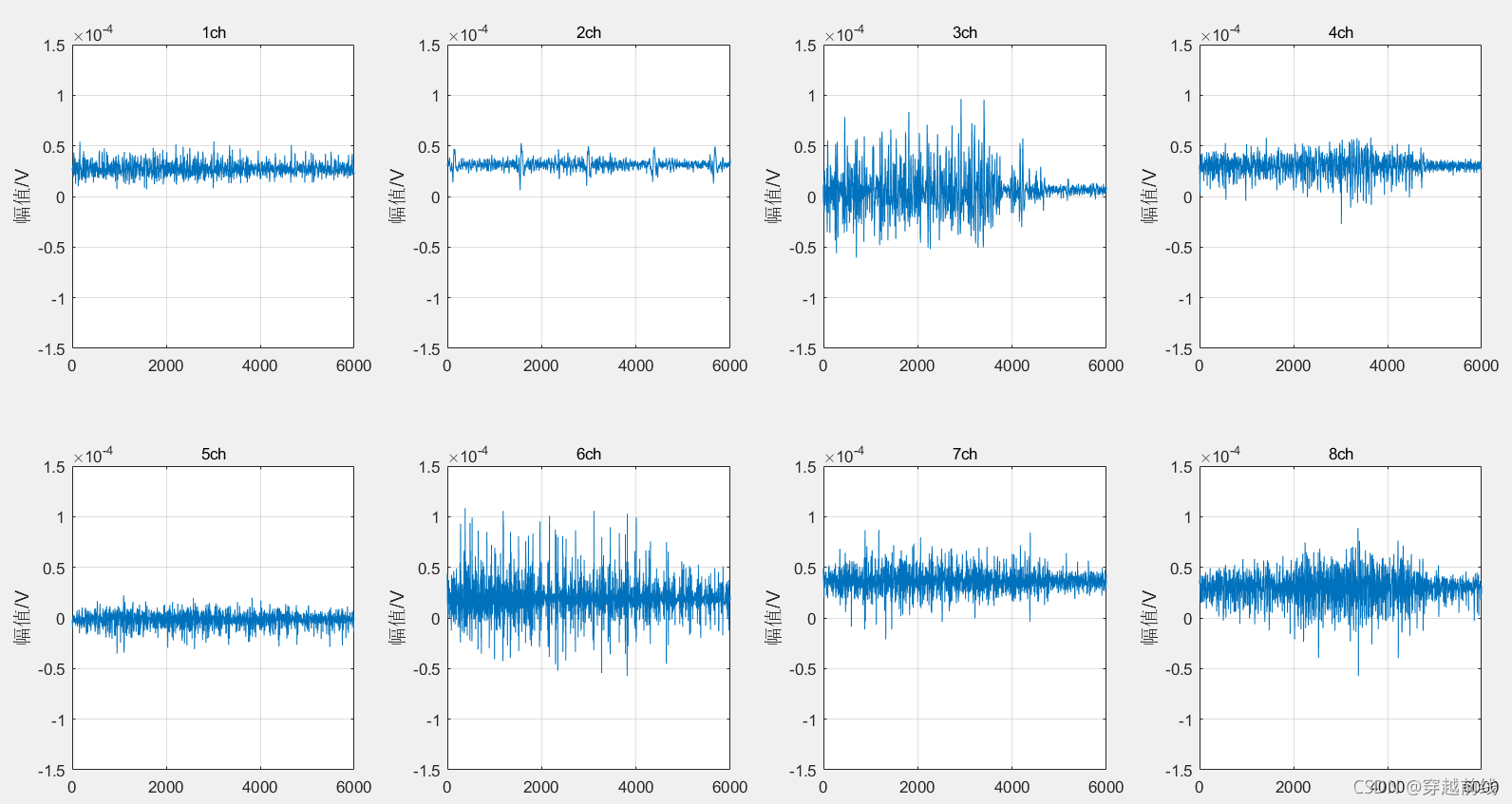
一下是静息动作和5个子动作的原始时域图如下所示。
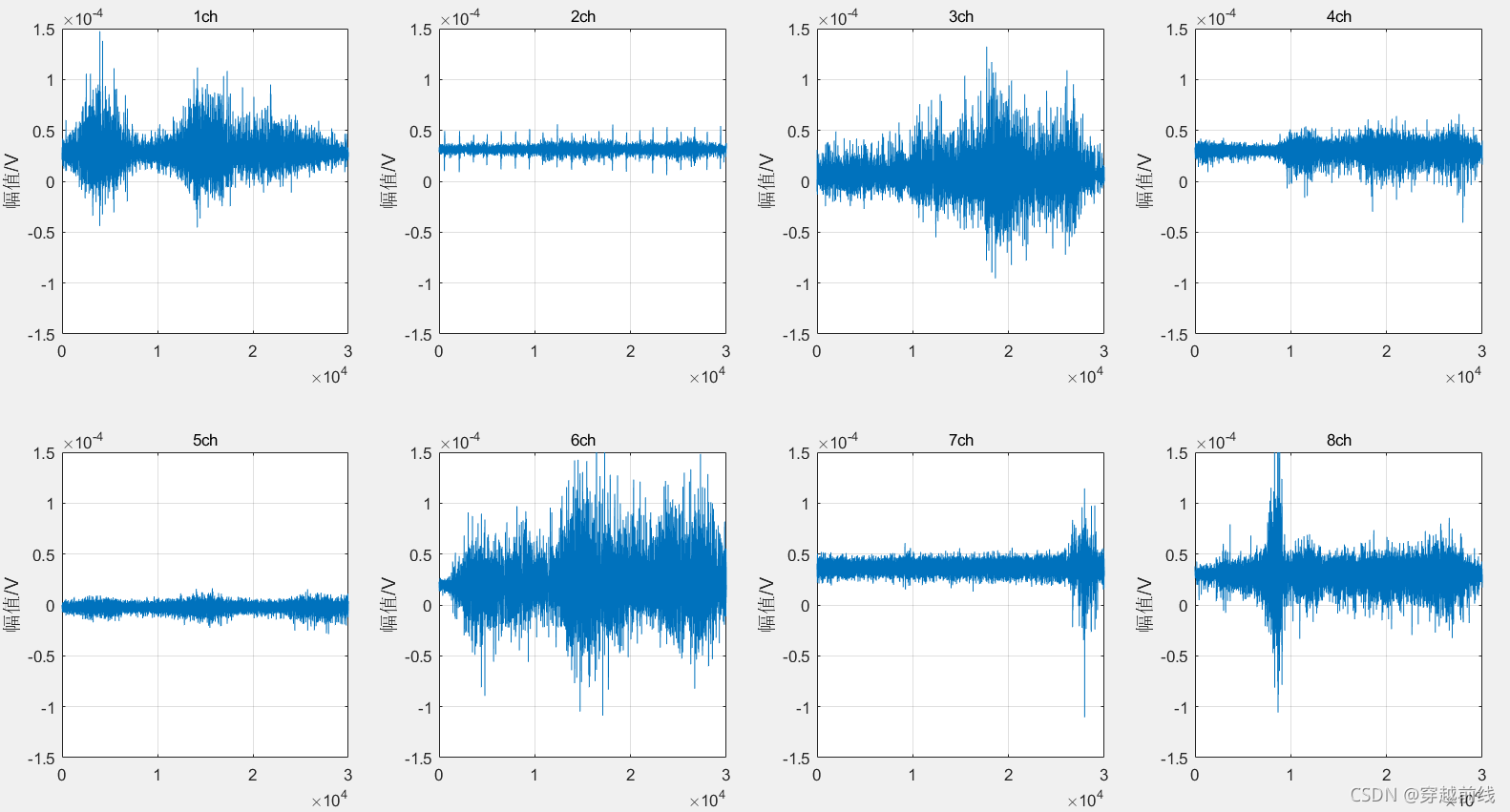
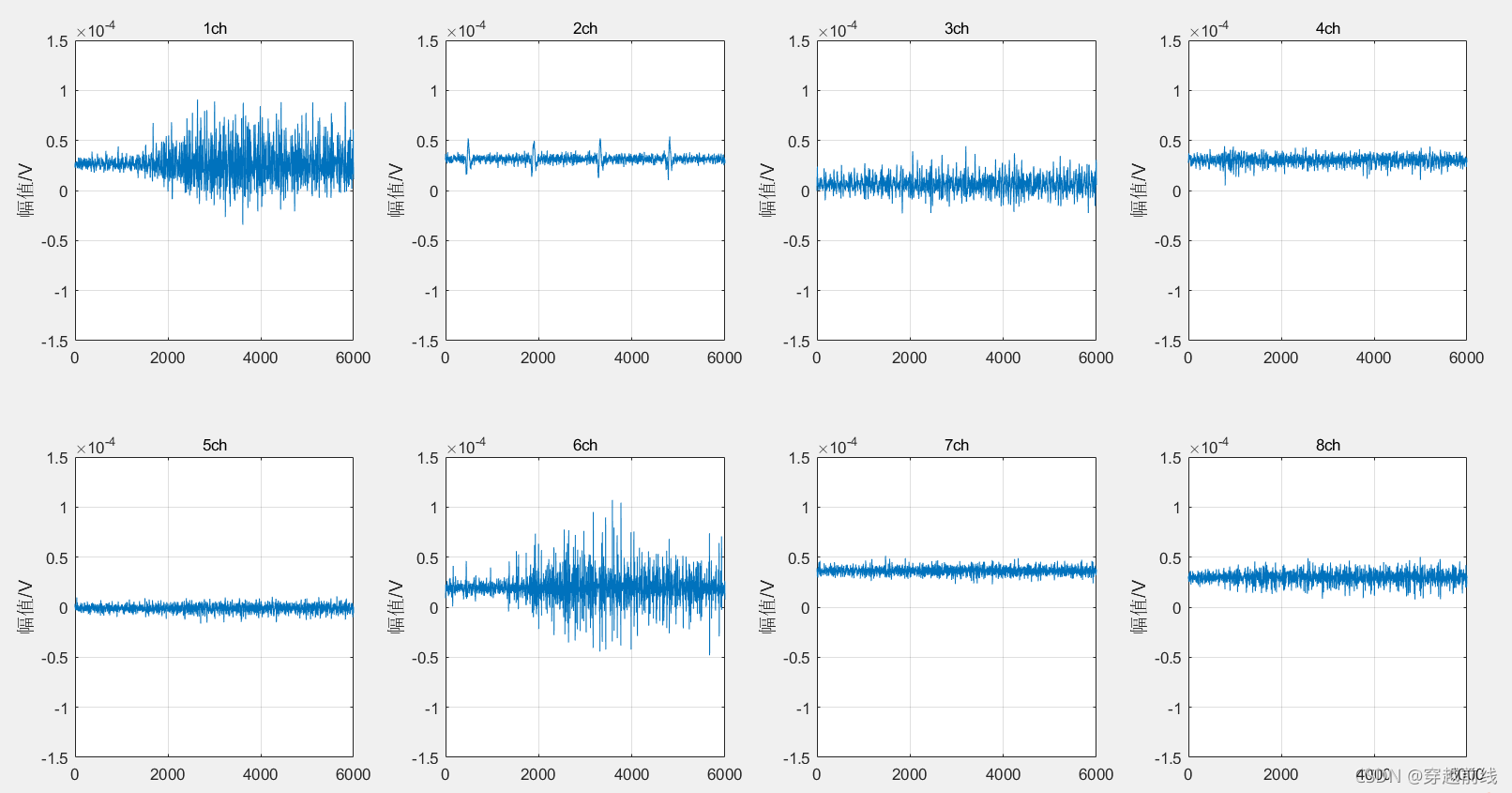
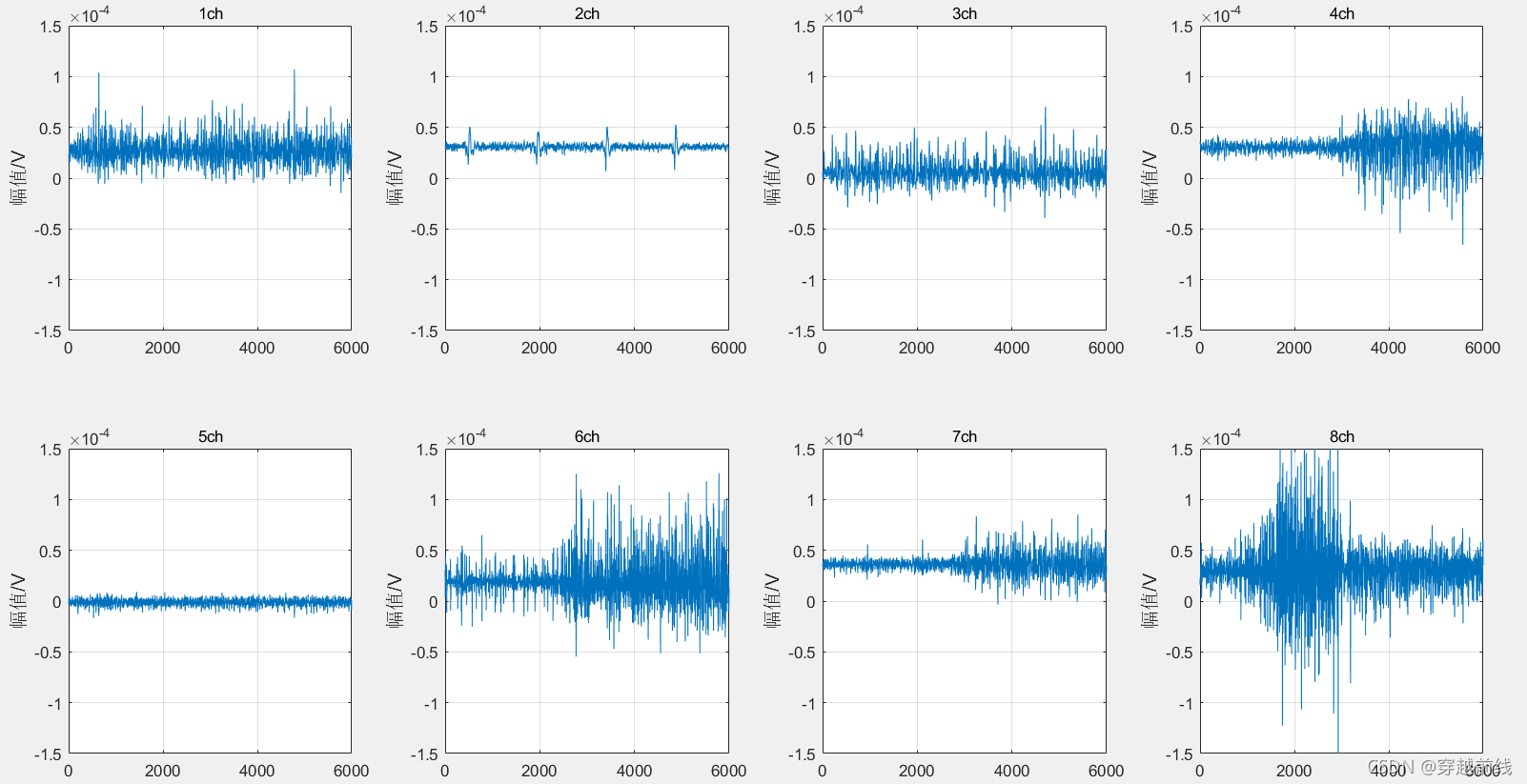
1.2 EEG数据显示
在1.1中展示了sEMG数据显示的过程与输出的原始时域图。在本节中实现的是脑电数据EEG的显示。本文选用的是64导联脑电帽，但是在采集过程中使用的是其中的32个通道。在本文课题中大脑进行的工作主要是对于拿水杯动作的想象。而根据对脑区功能的划分，与运动想象相关度最大的为C3,C4通道，因此选取这两个通道为主要研究对象并展示它们的原始时域图
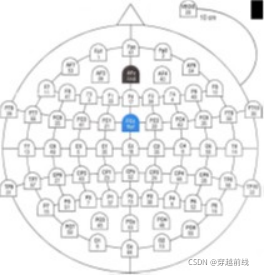
其中中心点Cz是失状线和冠状线的交点，因而常作为基准点
VEOG是垂直眼电电极，常用于记录眨眼伪迹。
因此Cz与VEOG待会儿会与C3,C4共同显示出原始时域图
显示EEG原始时域图所需的matlab代码如下所示
clear;
clc;
filename='/matlab.2019a/bin/paper review/EEG数据存放/1上肢动作/1上肢动作24.csv'
P=csvread(filename);%从第1行第0列开始读取数据figure(1);%Create figure window
%% 读取并显示C3通道数据
EEG=P(:,5);%获取一个通道的肌电数据
EEG_l=length(EEG);%获取一个通道的数据量
n = 0:EEG_l-1;%横坐标数值
subplot(4, 1, 1);
plot(n,EEG);
grid;%显示或隐藏轴网格线,切换主栅格线的可见性
% ylabel('幅值/V','FontSize',12);%y轴的标签
title('C3通道数据');
%% 读取并显示C4通道数据
EEG=P(:,6);%获取一个通道的肌电数据
EEG_l=length(EEG);%获取一个通道的数据量
n = 0:EEG_l-1;%横坐标数值
subplot(4, 1, 2);
plot(n,EEG);
grid;%显示或隐藏轴网格线,切换主栅格线的可见性
title('C4通道数据');
%% 读取并显示VEOG通道数据
EEG=P(:,20);%获取一个通道的肌电数据
sEMG_l=length(EEG);%获取一个通道的数据量
n = 0:EEG_l-1;%横坐标数值
subplot(4, 1, 3);
plot(n,EEG);
grid;%显示或隐藏轴网格线,切换主栅格线的可见性
title('VEOG通道数据');
%% 读取并显示Cz通道数据
EEG=P(:,18);%获取一个通道的肌电数据
sEMG_l=length(EEG);%获取一个通道的数据量
n = 0:EEG_l-1;%横坐标数值
subplot(4, 1, 4);
plot(n,EEG);
grid;%显示或隐藏轴网格线,切换主栅格线的可见性
title('VEOG通道数据');
原始脑电时域图如下所示
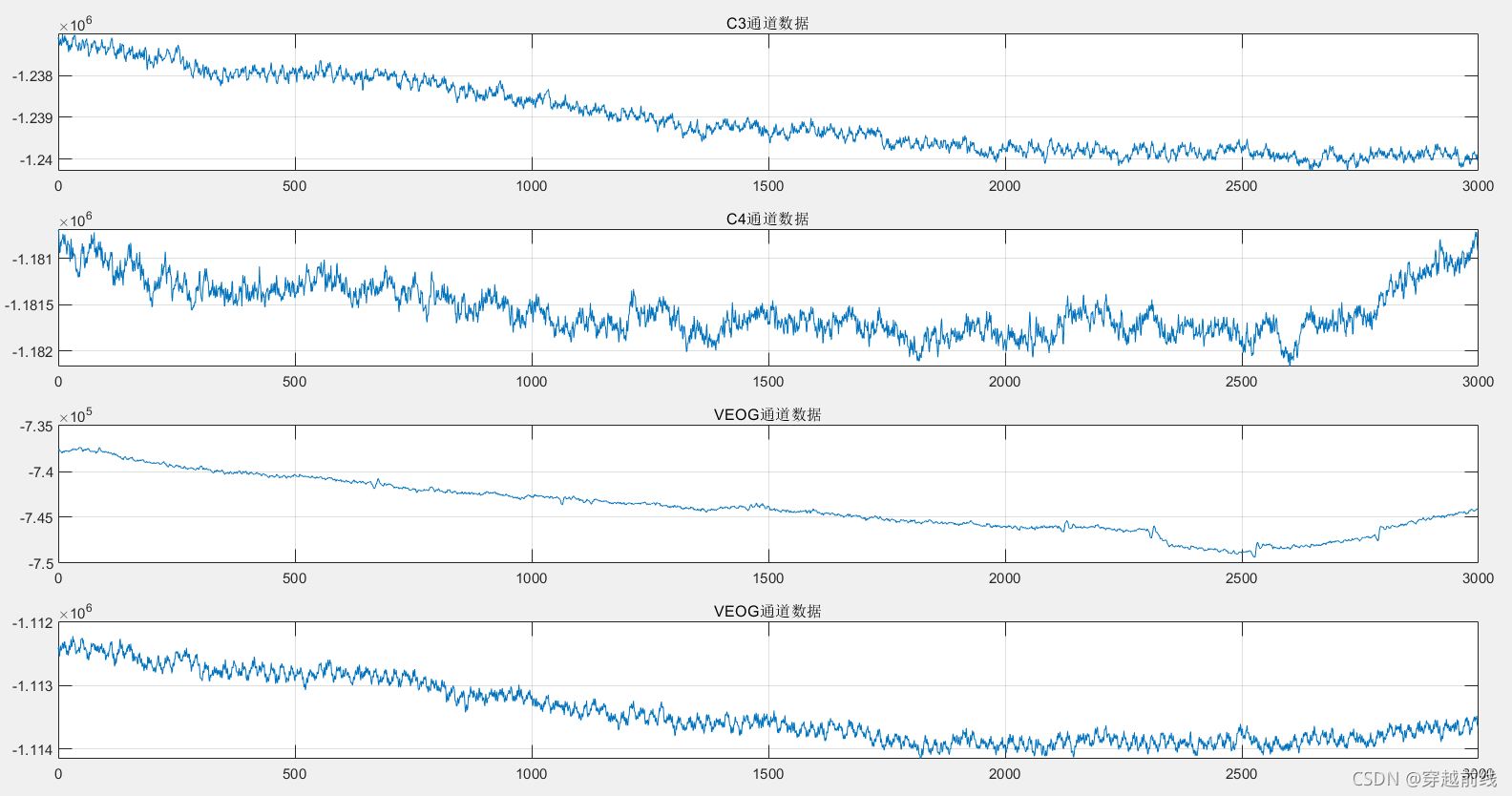
2 EEG与sEMG数据预处理
实验采集到的数据并不能直接使用，信号中还含有较多的噪声信号，为了得到干净的信号，就需要对信号做一定的处理工作。信号预处理的主要工作就是通过滤波，滤除信号中的无用信息，提高信号的信噪比，为后续的特征提取工作提供干净的信号，进一步提高动作分类的识别率。
2.1 肌电数据预处理
表面肌电信号具有信噪比低、随机性强、非平稳等特点，并且由于sEMG信号的采集机制，电极是放置于皮肤表面的，因此相对来说很容易受到皮肤的干燥程度，穿着衣服的松紧度，以及一系列的外部环境影响到我们所采集到的信号。根据我们对肌电信号的学习，我们了解到，肌电信号主要包含三种噪声。一，高斯白噪声，二，基线漂移，三，工频噪声。其中工频噪声的处理可以使用软件滤波的方式，也可以使用去噪硬件电路。由于我所采用的采集设备具有良好的去噪硬件电路，所以本文中便不再去除工频噪声。
2.1.1 傅里叶变换显示原始频域图
由于基线漂移是在频域中研究的，因此我们需要先使用傅里叶变换将原始时域图变换为频域图。将时域变换为频域所需要的傅里叶变换代码如下所示，由于各个通道的代码都一样，所以只展示Act1的代码。
%%%傅里叶变换，频谱图展示%%%
clear;
clc;
filename='/matlab.2019a/bin/paper review/sEMG数据存放/1上肢动作/1上肢动作24.csv'
P=csvread(filename,0,0);%从第1行第0列开始读取数据
[row, column]=size(P);%获取数据维度大小
SampleFre = 2000;%采样频率
ch_i=0;%switch计数
figure(1);%Create figure window
for column_i=1:8
ch_i=ch_i+1;
sEMG=P(:,column_i);%获取一个通道的肌电数据
sEMG_l = length(sEMG);%获取一个通道上数据长度
t = (0:sEMG_l-1)/SampleFre;%频率的倒数为时间
sEMG_fft = fft(sEMG);%对信号进行傅里叶变换，此时的数据为对称的复数，需要进行一些
sEMG_fft_single = 2 * abs(sEMG_fft(1:length(sEMG_fft)/2)) / length(sEMG_fft)
Frequence_single = SampleFre * (1:length(sEMG_fft)/2) / length(sEMG_fft);
subplot(2, 4, ch_i);
plot(Frequence_single, sEMG_fft_single);
grid;
ylabel('幅值/V','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
title(sprintf('%dch',ch_i),'FontSize',30, 'FontWeight', 'bold');% 设置肢体大
axis([0 1000 0 3*10^(-6)])
end
将代码运行，得到以下五个子动作的原始频域图
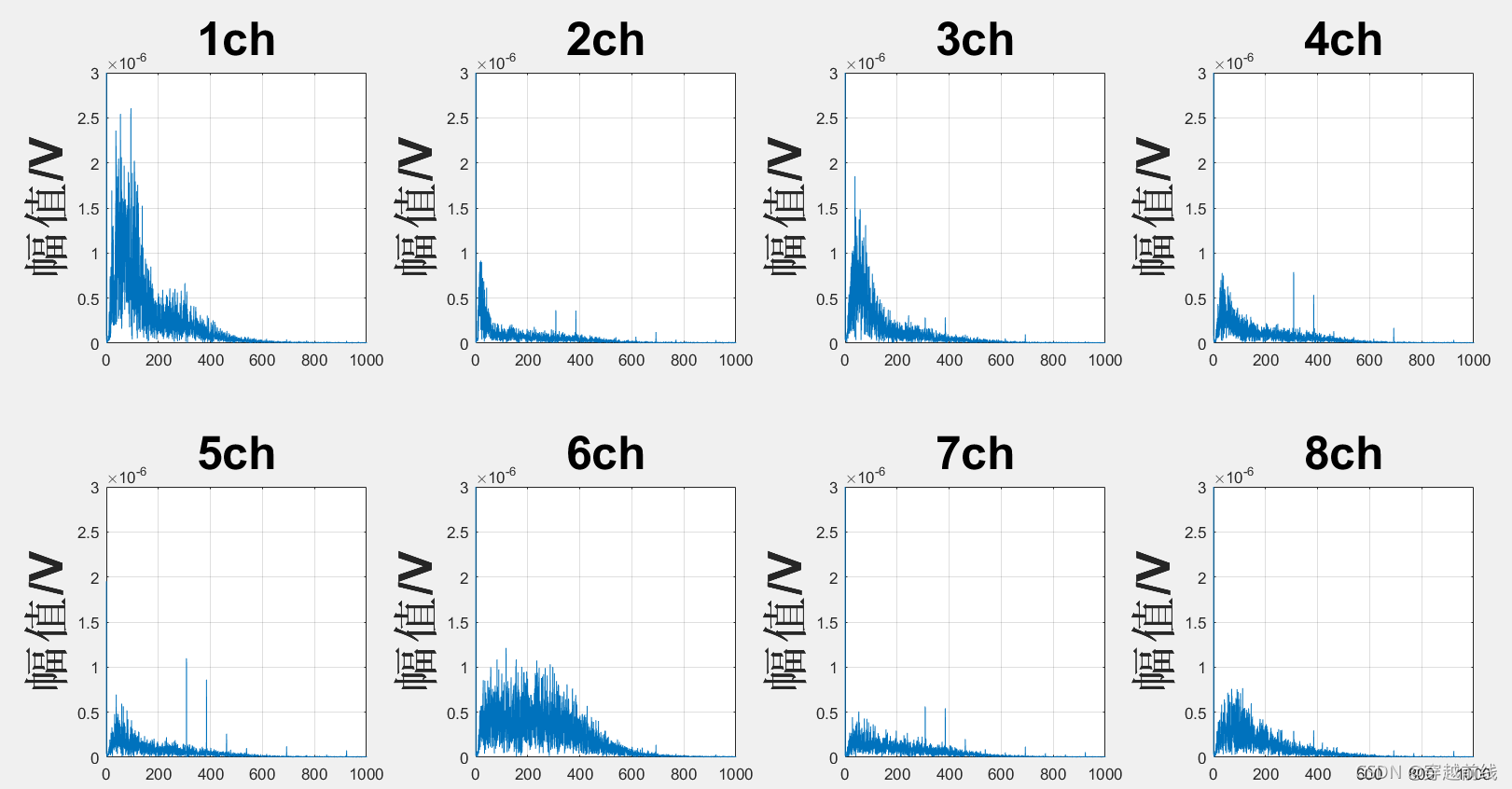
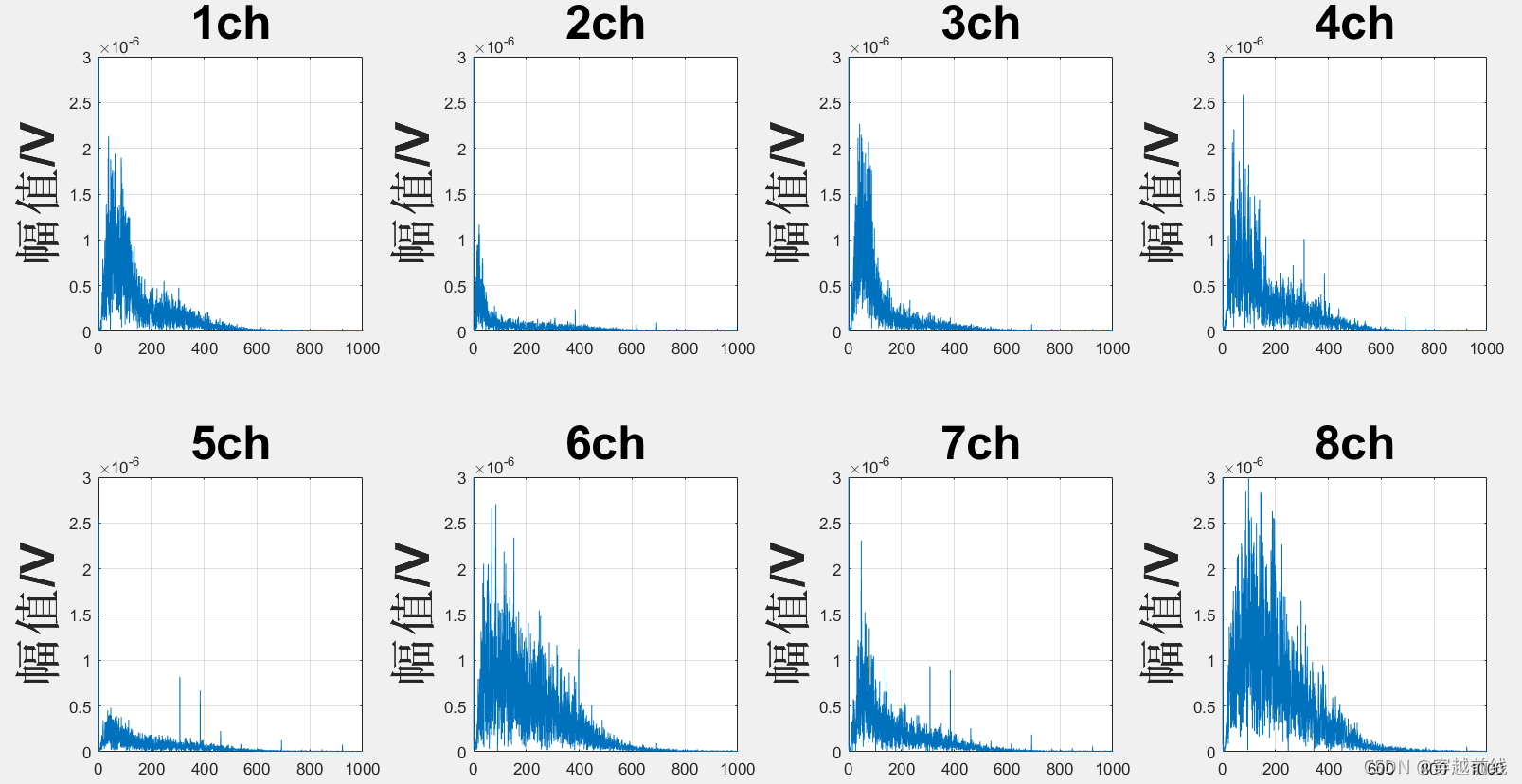
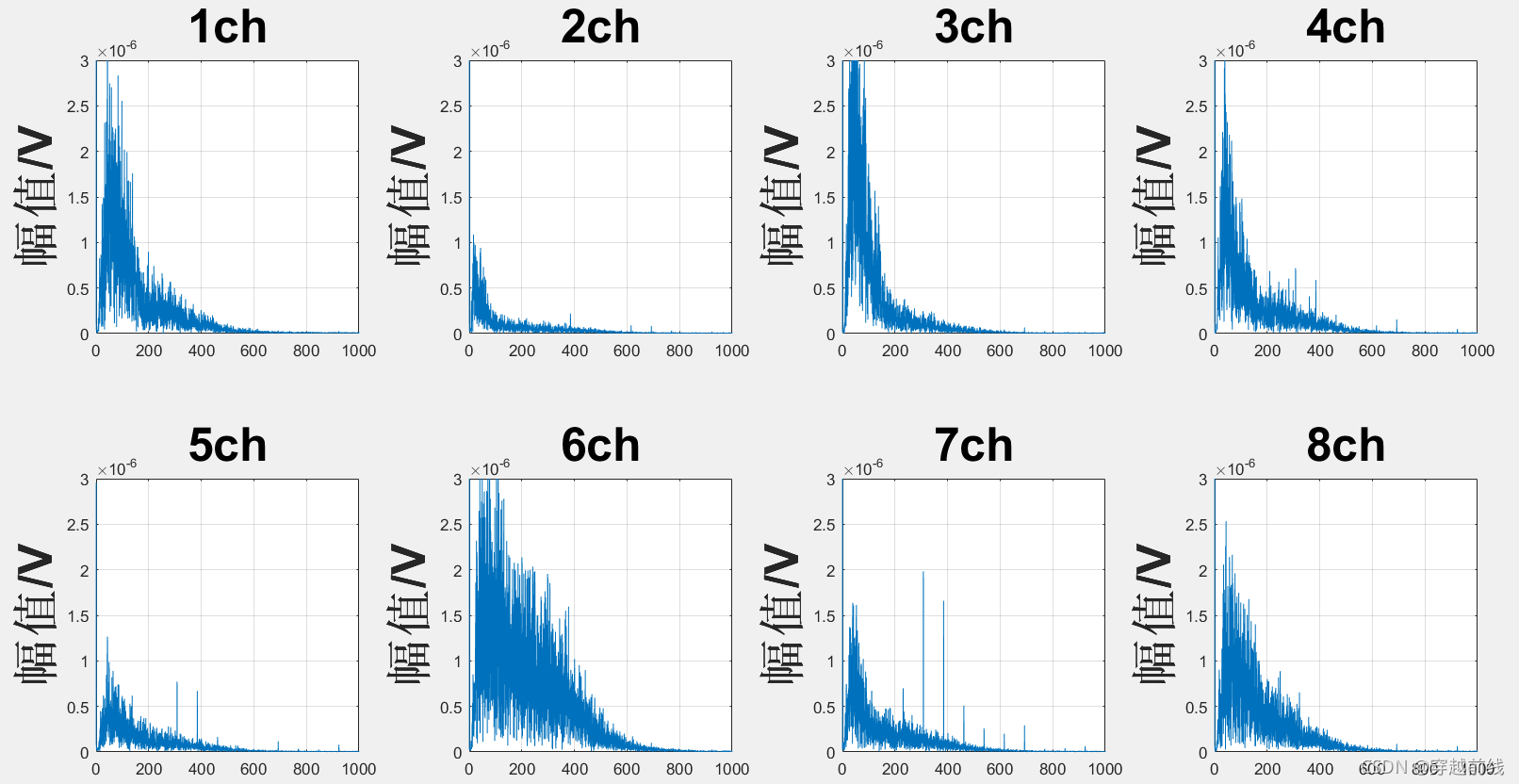
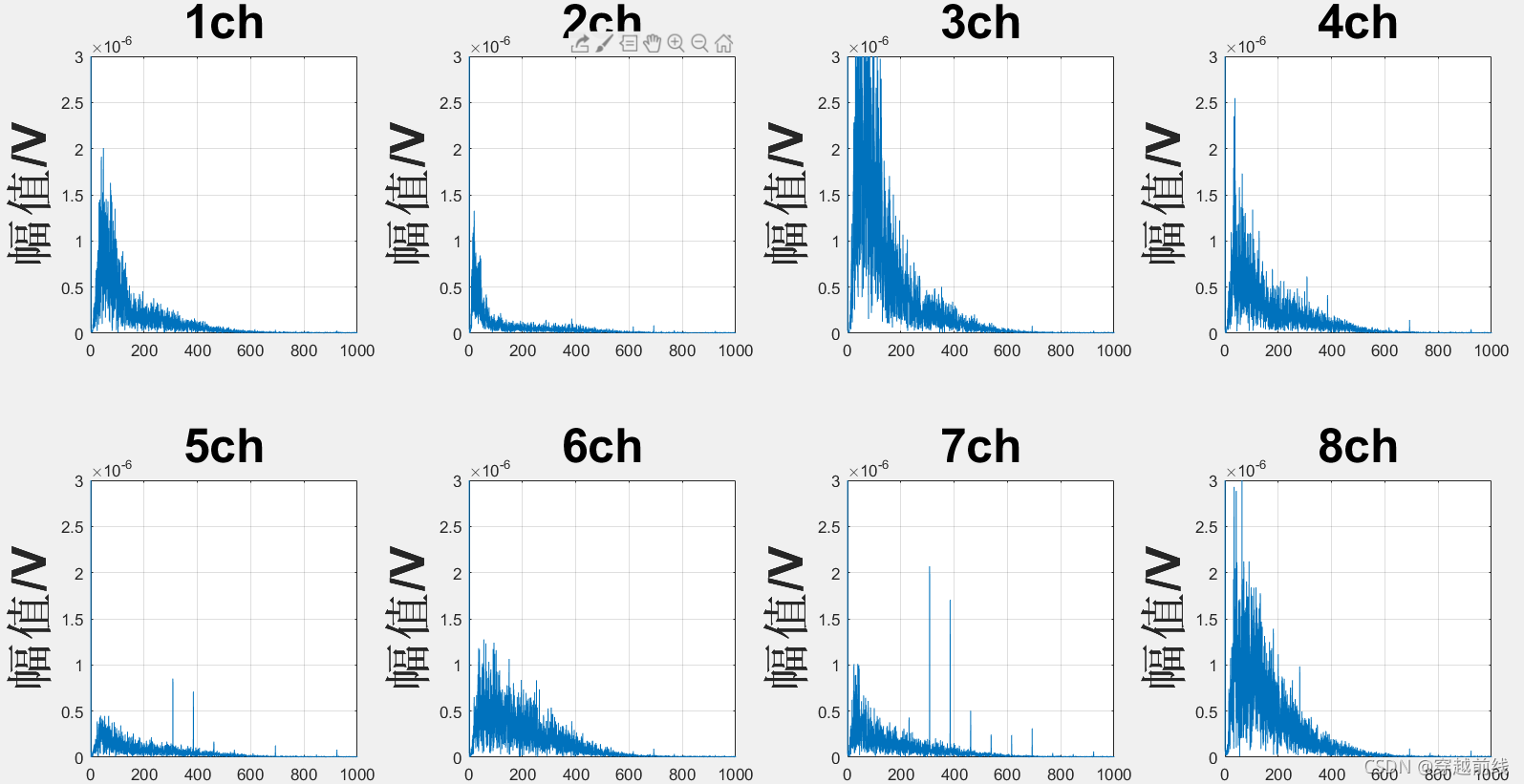
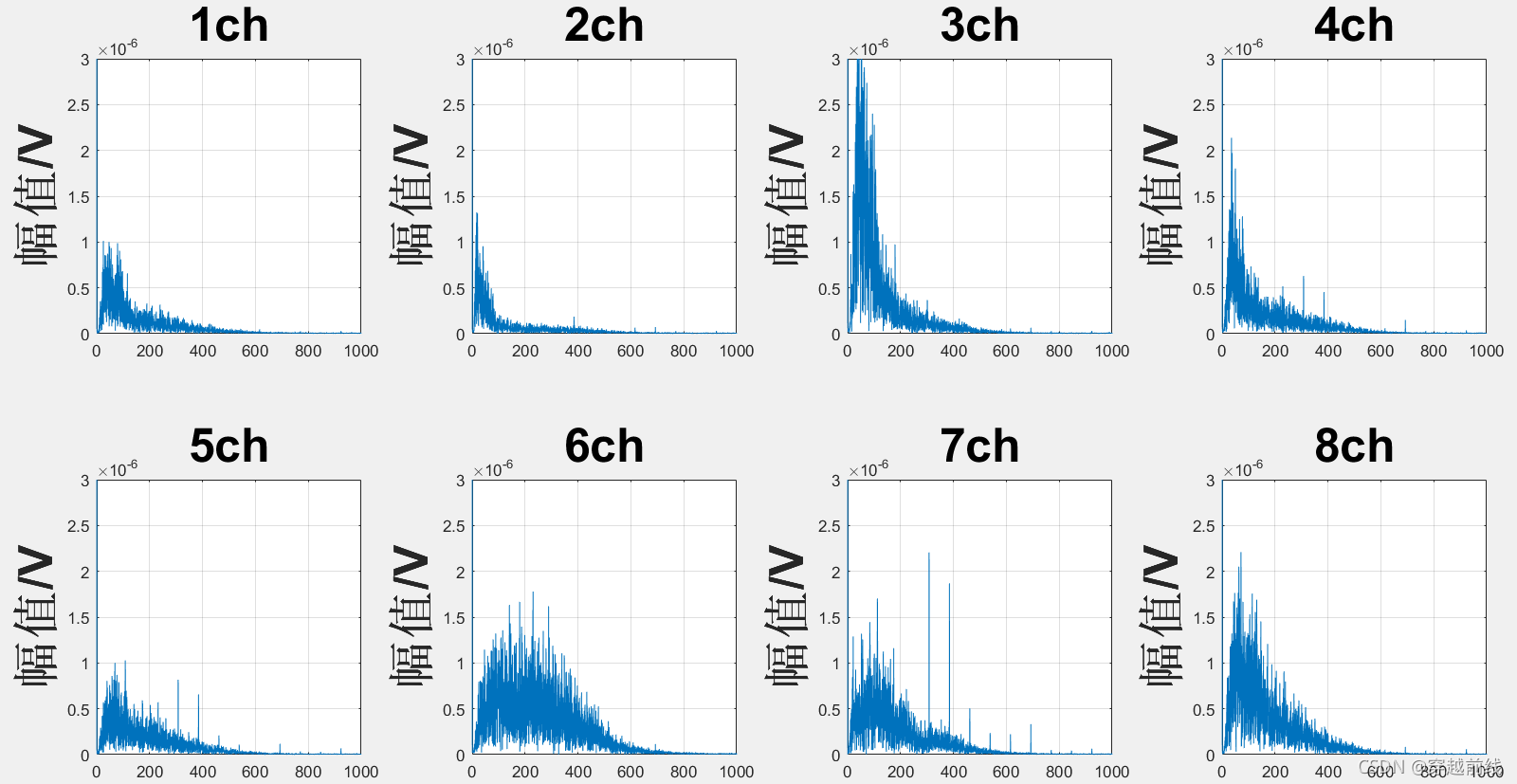
根据分析，我们不难看出，这些信号的原始频域图都在低频域有很大的幅值，很显然这并不是我们想要的。而造成这种现象的原因正是因为基线漂移，因此，我们必须采取措施去除基线漂移的影响。
2.1.2 小波去噪法
通过上面的分析，我们已经知道了，我们所采集的sEMG信号受到了基线漂移的影响，因此我们需要想办法将其消除，因此在本节的内容中引入了小波去噪法。
本文主要分析与探讨的是小波变换阈值去噪（WTD）和基于小波变换数字滤波阈值去噪（WDFTD）对肌电信号的滤波效果，主要分析两种滤波器的优点和缺点，期望寻求一种效果最好的滤波器。
（一）基于小波变换的阈值去噪
小波阈值变换去噪是进行表面肌电信号滤波常用的一种方法。有用信号通常表现为低频信号，而噪声信号通常表现为高频信号在对信号进行小波分解后有用信号和噪声信号的小波系数的特点不一样，有用信号的小波系数大且数量少，噪声信号的小波系数小且数量多。本文利用基于小波变换的阈值去噪法去除sEMG高频噪声主要步骤如下：
第一步：对采集的表面肌电信号进行小波分解，确定分解层数和小波函数。本文选择sym6函数作为信号滤波的小波函数，并通过实验得出选择4层分解能过得到比较好的滤波效果。
第二步：选择阈值估计方法。本文选择启发式阈值（heursure），同时选择了mln标志。
第三步：信号重构，将小波分解后的底层的系数和各层的细节系数进行重构，得到重构后的时、频域信号。
根据以上步骤设计matlb代码实现小波变换的阈值去噪，代码如下。
%%%肌电WDT降噪效果分析%%%
clear;
clc;
SampleFre = 2000;%采样频率
filename='/matlab.2019a/bin/paper review/sEMG数据存放/1上肢动作/1上肢动作24.csv'
P=csvread(filename,0,0);%从第1行第0列开始读取数据
[row, column]=size(P);%获取数据维度大小
sEMG=P(:,1);%获取第一个通道的肌电数据
sEMG_l=length(sEMG);%获取第一个通道的数据量
%% WTD降噪后单一评价指标的计算 %%
[XD_WTD,CXD,LXD]=wden(sEMG, 'heursure', 's', 'mln', 4, 'sym6');%对信号进行小波变换
figure(1);%Create figure window
% 展示WTD降噪后信号
subplot(2, 1, 1);
plot(XD_WTD);
base_line = zeros(1,sEMG_l);
hold on;
plot(base_line, 'r');
title('时域信号','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
ylabel('幅值/V','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
% 展示WTD降噪后幅频信号
subplot(2, 1, 2);
t = (0:sEMG_l-1)/SampleFre;%频率的倒数为时间
sEMG_fft = fft(XD_WTD);%对信号进行傅里叶变换，此时的数据为对称的复数，需要进行一些变换
sEMG_fft_single = 2 * abs(sEMG_fft(1:length(sEMG_fft)/2)) / length(sEMG_fft);
Frequence_single = SampleFre * (1:length(sEMG_fft)/2) / length(sEMG_fft);
plot(Frequence_single, sEMG_fft_single);
ylabel('幅值/V','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
title('频域信号','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
axis([0 1000 0 3*10^(-6)])
sEMG_f(1:sEMG_l-1) = sEMG(1:sEMG_l-1);%为平滑度准备数据
sEMG_b(1:sEMG_l-1) = sEMG(2:sEMG_l);
XD_f(1:sEMG_l-1) = XD_WTD(1:sEMG_l-1);
XD_b(1:sEMG_l-1) = XD_WTD(2:sEMG_l);
RMSE_WTD = sqrt(sum((sEMG-XD_WTD).^2)/sEMG_l);%计算均方根误差
SNR_WTD = 10*log10((sum(XD_WTD.^2)/sEMG_l)/(sum((sEMG-XD_WTD).^2)/sEMG_l));%计算
r_WTD = sum((XD_b-XD_f).^2)/sum((sEMG_b-sEMG_f).^2);%计算平滑度
%输出单个评价指标的值
fprintf('WTD的RMSE(均方根)：\t%f\n', RMSE_WTD);
fprintf('WTD的SNR(信噪比)：\t%f\n', SNR_WTD);
fprintf('WTD的r(平滑度)：\t%f\n', r_WTD);
运行代码可以得到经过小波变换阈值去噪后的时域图与频域图，并得到相应的评价指标。各动作小波变换阈值去噪法所得时频域图及评价指标如下所示。
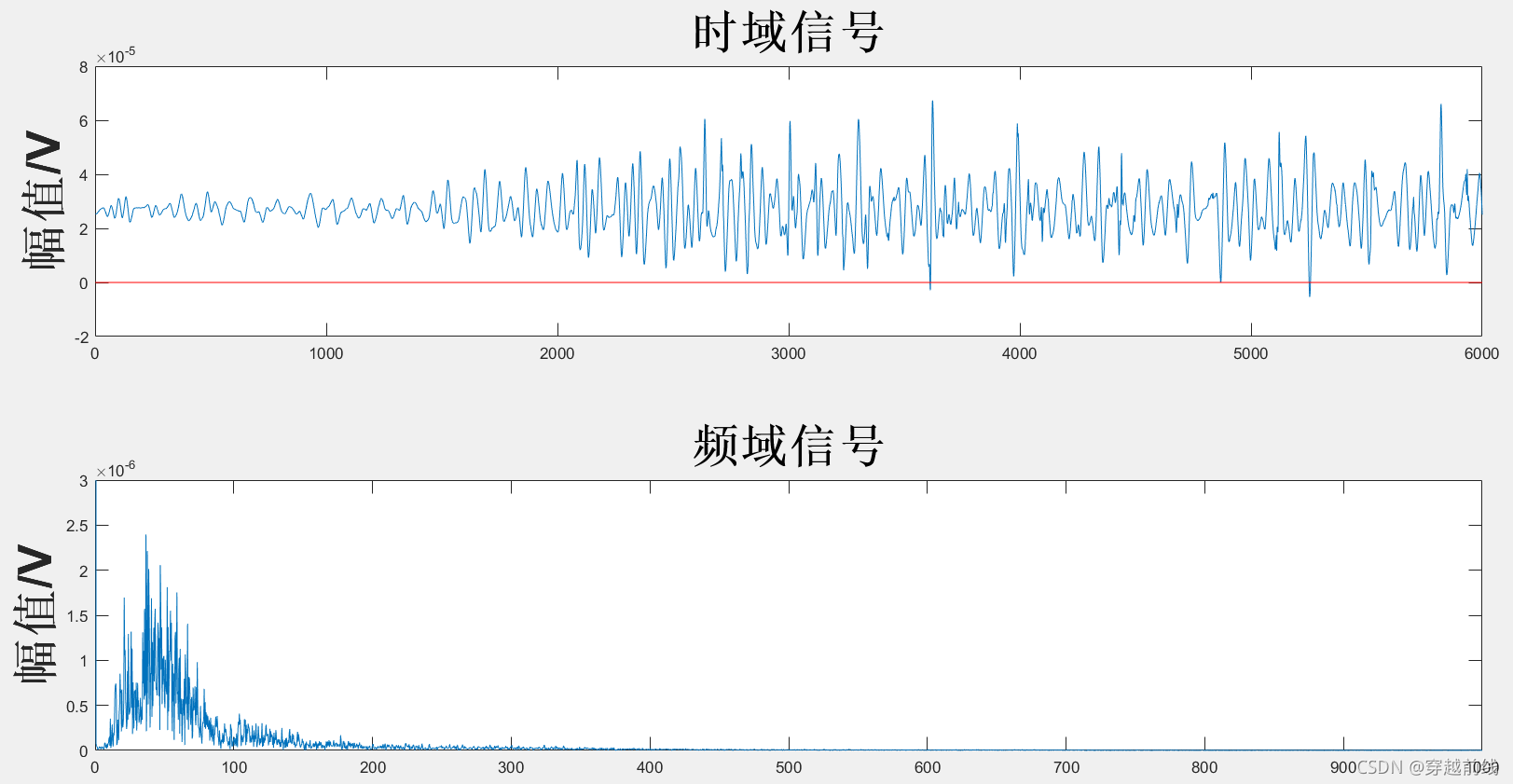
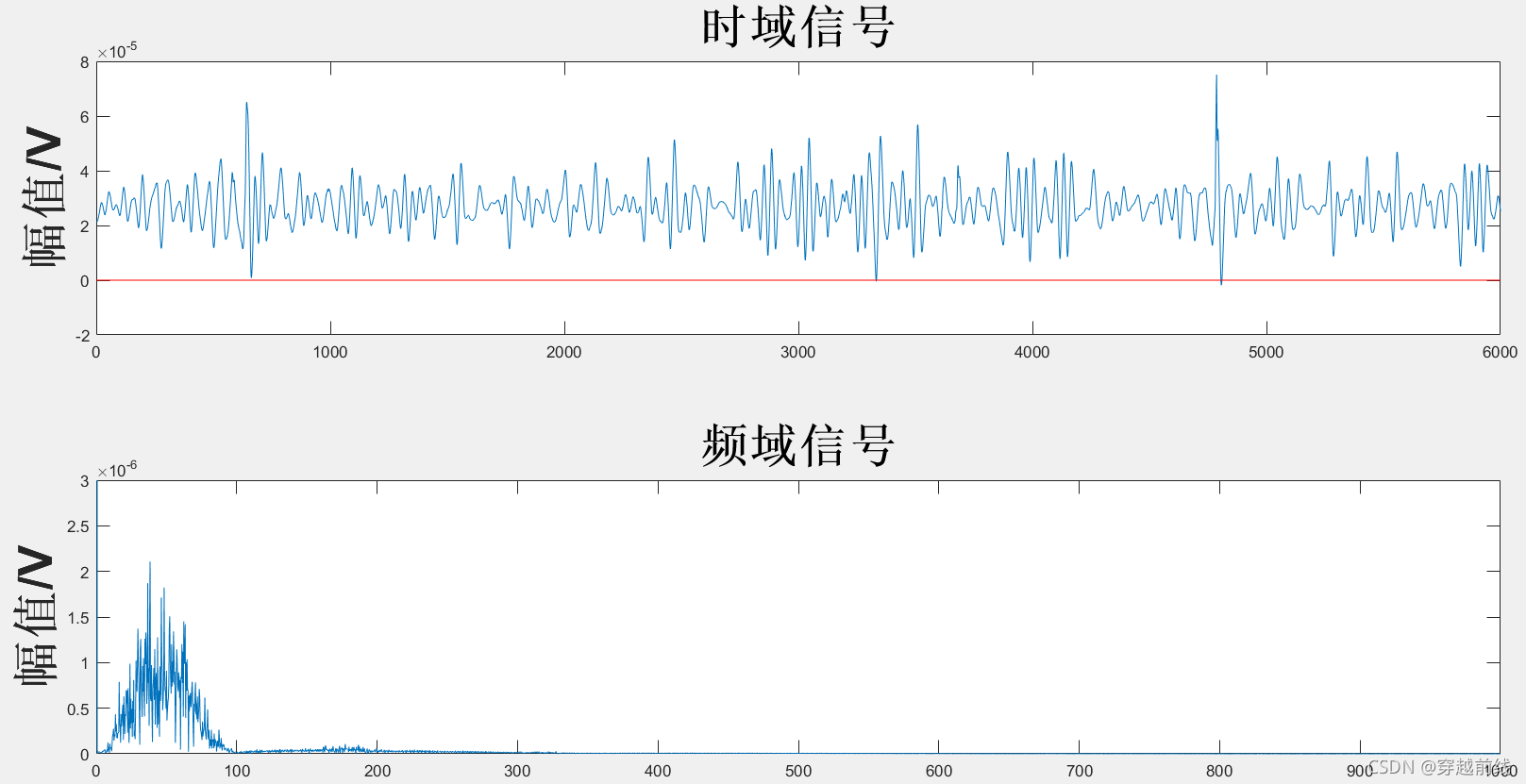
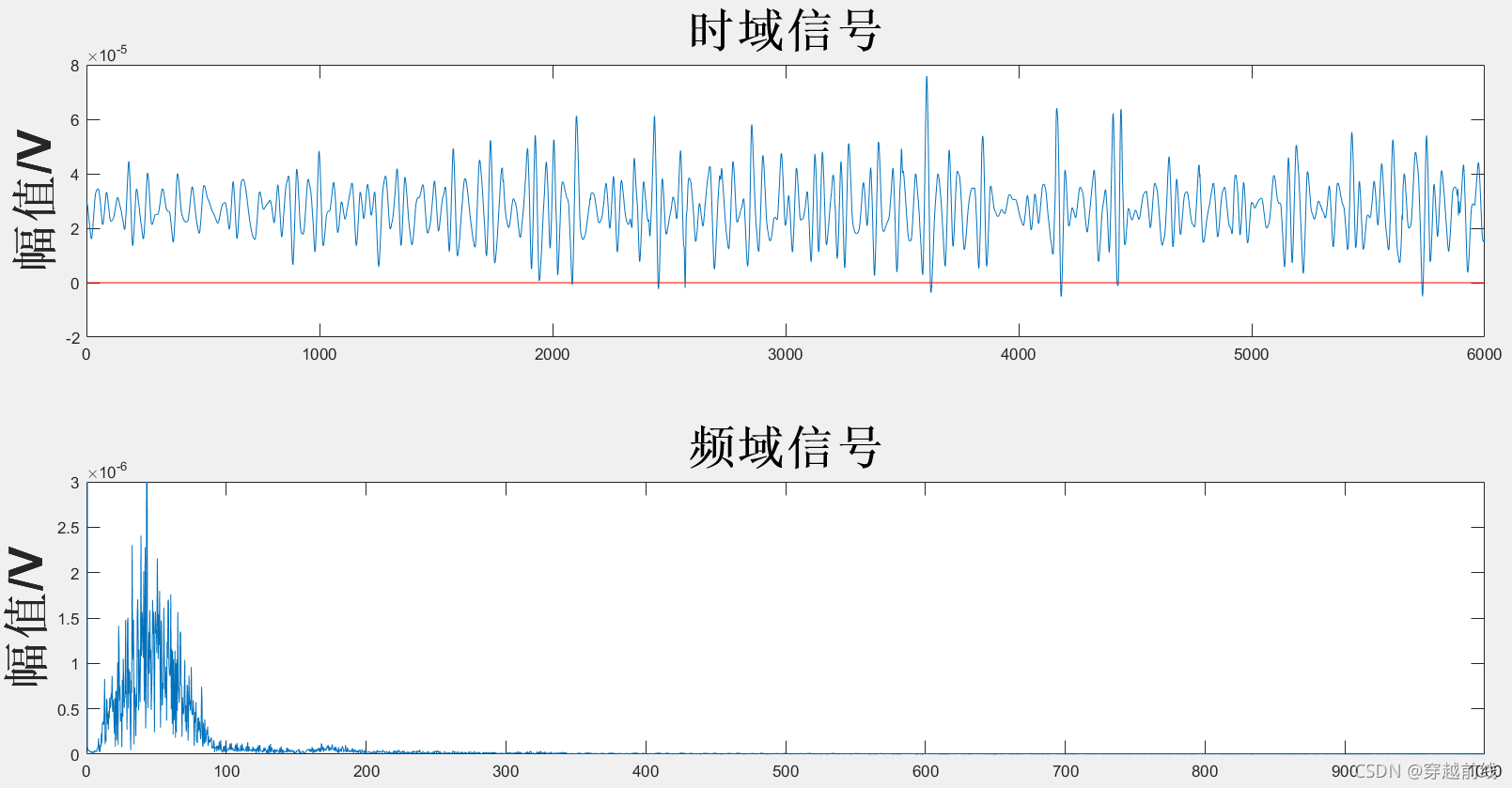
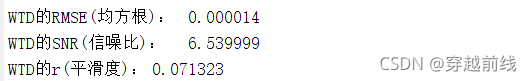
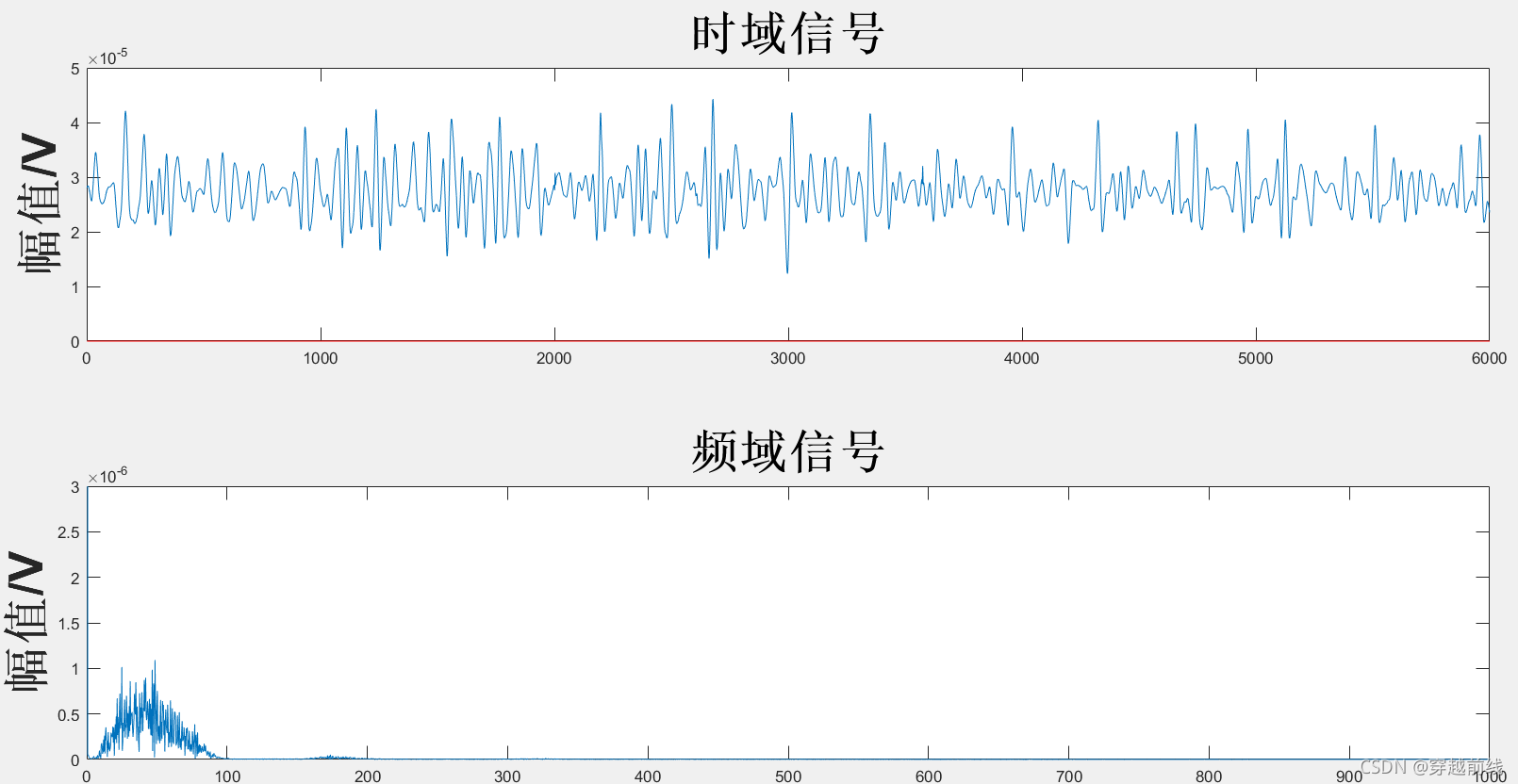
以上图中的红线代表幅值的0点，可以发现WTD并没有去掉表面肌电信号的基线漂移。同时也可以发现，原始信号的尖端毛刺变少了，频谱图的高频部分幅值很小（图中没有表示出来，因为基线的频率幅值太大了），WTD滤除高频噪声的效果很好。从WTD滤波后的信号的评价指标来看，滤波后的信号平滑度和信噪比的数值都在可以接受的范围内。
(二)基于小波变换数字滤波阈值去噪
基于小波变换数字滤波阈值去噪是将小波阈值.去噪和数字滤波器组合所得。肌电信号的有用频段主要集中在0HZ-500HZ，除了工频噪声之外还含有直流分量的噪声以及多数高斯白噪声。Delsys无线表面肌电采集系统采样频率为2000HZ，根据香农采样定理可得， 采集到的表面肌电信号的最高频率为1000HZ。
对采集到的信号进行5层分解，可以得到各个小波系数的频率范围如下表所示。表中的a5(n)代表直流分量，在进行小波重构时将其设置为0可消除肌电信号的基线漂移问题。表中d1(n)代表高频信号，肌电信号的频率主要在0-500HZ,所以将d1(n)置0,可以消除高频噪声。
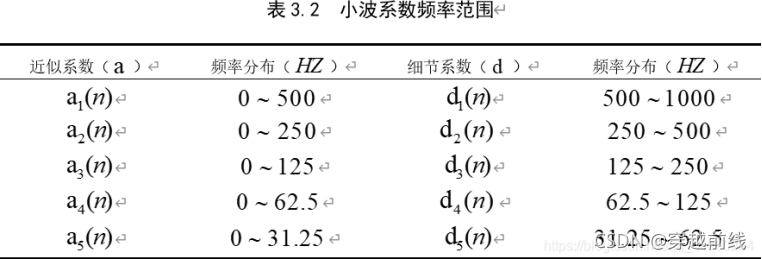
matlab实现小波变换数字滤波阈值去噪所需要代码如下所示：
%%%肌电WDFTD降噪效果分析%%%
clear;
clc;
SampleFre = 2000;%采样频率
filename='/matlab.2019a/bin/paper review/sEMG数据存放/1上肢动作/1上肢动作24.csv'
P=csvread(filename,0,0);%从第1行第0列开始读取数据
[row, column]=size(P);%获取数据维度大小
sEMG=P(:,1);%获取第一个通道的肌电数据
sEMG_l=length(sEMG);%获取第一个通道的数据量
%% WDFTD降噪后单一评价指标的计算 %%
[C,L]=wavedec(sEMG,5,'sym6');%多级一维小波分解 改分解层数
ca5=appcoef(C,L,'sym6',5);%一维近似系数，计算一维信号的近似系数
[cd1,cd2,cd3,cd4,cd5]=detcoef(C,L,[1,2,3,4,5]);%一维细节系数，获取小波分解的细节系数
%利用数字滤波阈值 去除基线漂移 和 高频信号降噪
%将第一层细节系数设置为0，进行高频信号降噪，将最后一层的近似系数设置为0，进行基线漂移的
C5=[zeros(size(ca5)); cd5; cd4; cd3; cd2; zeros(size(cd1))];
% C5=[ca5; cd5; cd4; cd3; cd2; zeros(size(cd1))];%没有去除基线漂移
sEMG_wavelet=waverec(C5,L,'sym6');%多层次一维小波重构
figure(1);%Create figure window
% 展示WDFTD降噪后信号
subplot(2, 1, 1);
plot(sEMG_wavelet);
base_line = zeros(1,sEMG_l);
hold on;
plot(base_line, 'r');
title('时域信号','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
ylabel('幅值/V','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
% 展示WDFTD降噪后幅频信号
subplot(2, 1, 2);
t = (0:sEMG_l-1)/SampleFre;%频率的倒数为时间
sEMG_fft = fft(sEMG_wavelet);%对信号进行傅里叶变换，此时的数据为对称的复数，需要进行
sEMG_fft_single = 2 * abs(sEMG_fft(1:length(sEMG_fft)/2)) / length(sEMG_fft);
Frequence_single = SampleFre * (1:length(sEMG_fft)/2) / length(sEMG_fft);
plot(Frequence_single, sEMG_fft_single);
ylabel('幅值/V','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
title('频域信号','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
axis([0 1000 0 3*10^(-6)])
sEMG_f(1:sEMG_l-1) = sEMG(1:sEMG_l-1);%为平滑度准备数据
sEMG_b(1:sEMG_l-1) = sEMG(2:sEMG_l);
sEMG_wavelet_f(1:sEMG_l-1) = sEMG_wavelet(1:sEMG_l-1);
sEMG_wavelet_b(1:sEMG_l-1) = sEMG_wavelet(2:sEMG_l);
RMSE_WDFTD = sqrt(sum((sEMG-sEMG_wavelet).^2)/sEMG_l);%计算均方根误差
SNR_WDFTD =10*log10((sum(sEMG_wavelet.^2)/sEMG_l)/(sum((sEMG-mean(sEMG))-sEMG_l)));
r_WDFTD = sum((sEMG_wavelet_b-sEMG_wavelet_f).^2)/sum((sEMG_b-sEMG_f).^2);%计算
% 输出单个评价指标的值
fprintf('WTD的RMSE(均方根)：\t%f\n', RMSE_WDFTD);
fprintf('WTD的SNR(信噪比)：\t%f\n', SNR_WDFTD);
fprintf('WTD的r(平滑度)：\t%f\n', r_WDFTD);
运行matlab代码可以得到WDFTD滤波器下去噪后的图像，如下所示
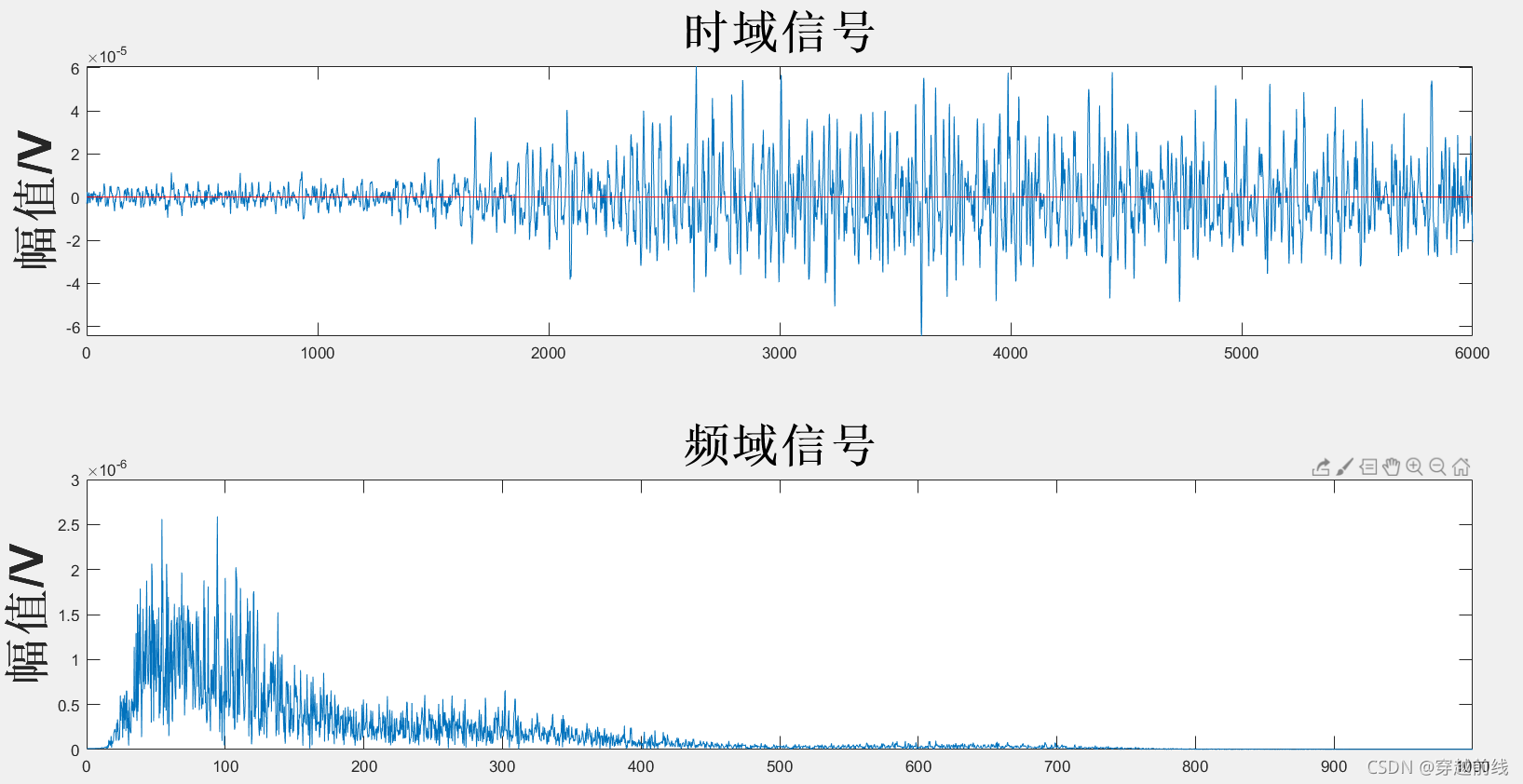
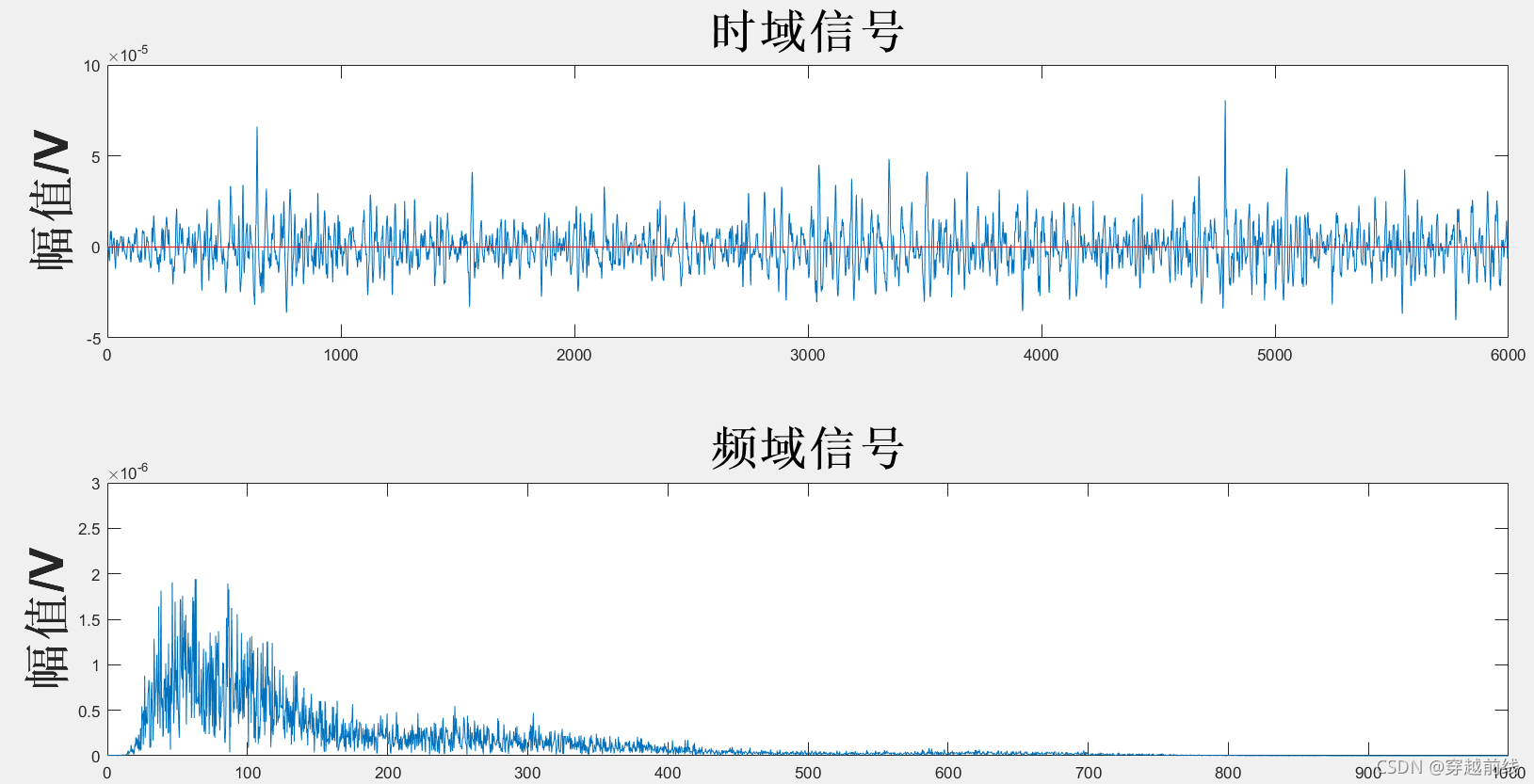
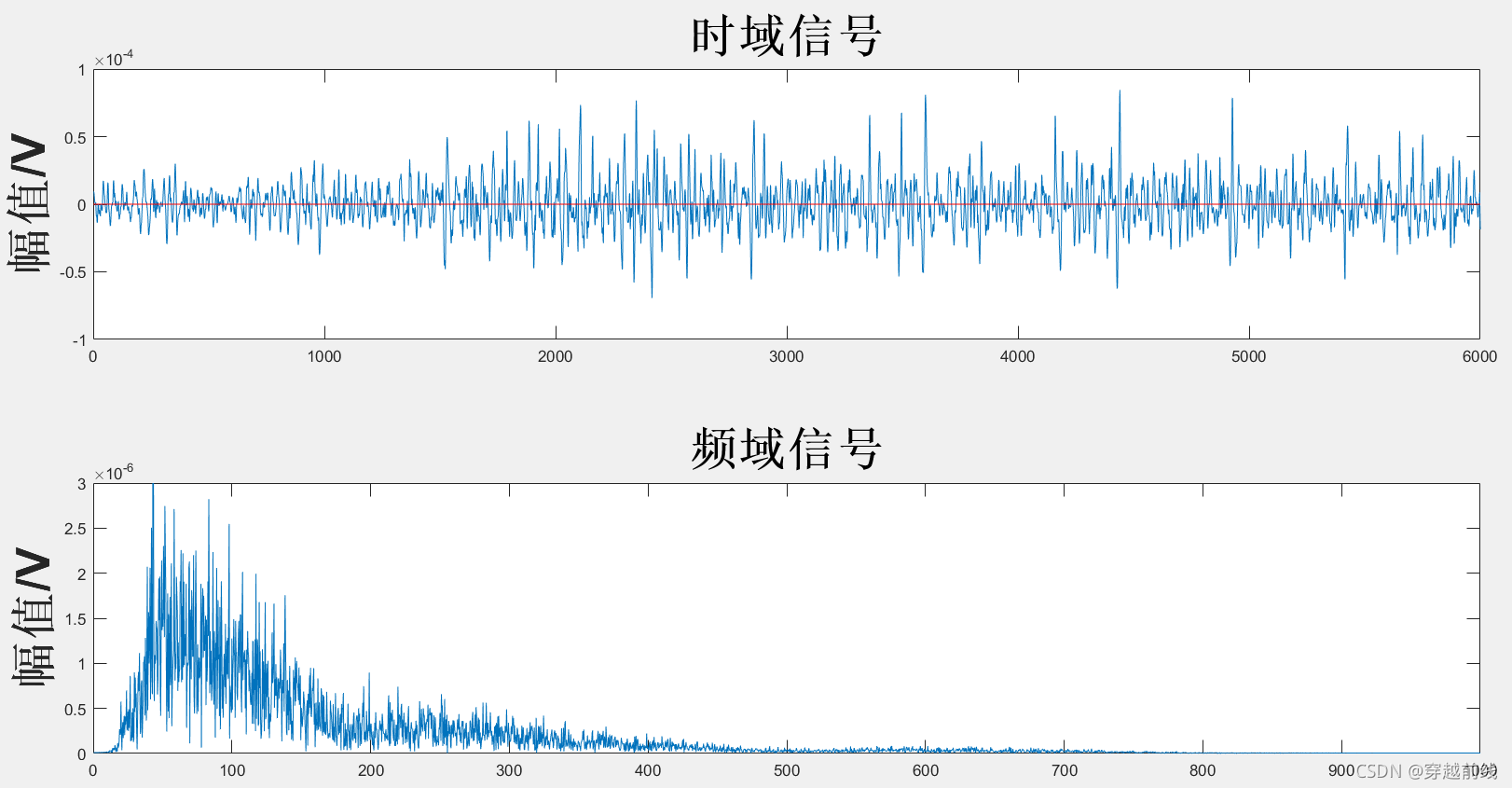
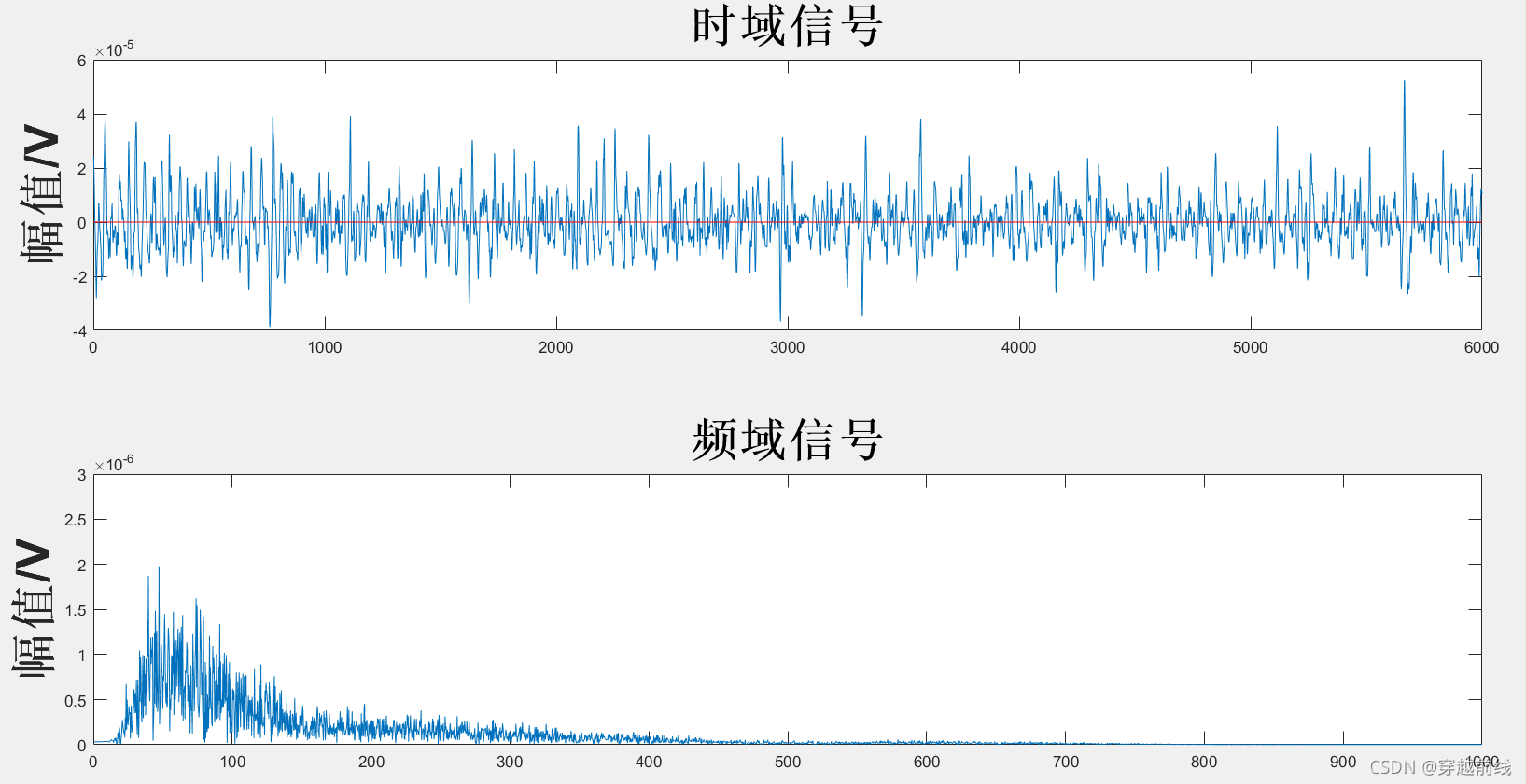
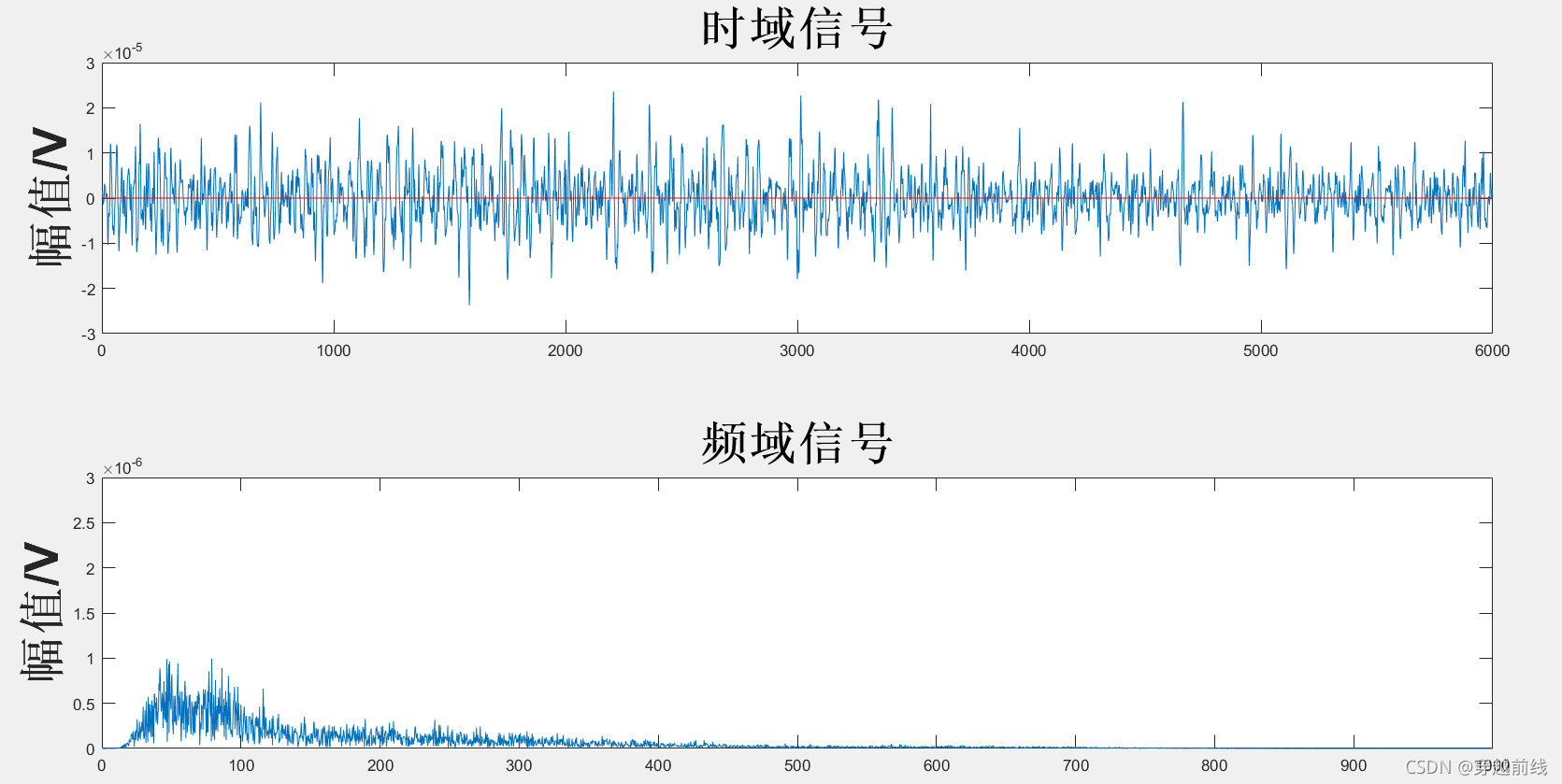
经过观察分析WDFTD滤波后的sEMG的时域图，图中红线代表及电信号的幅值的基线， 由图可以看到WDFTD滤波器可以去除表面肌电信号的基线漂移，但是从图中频域信号来看，WDFTD滤波器去除高频信号的能力相比于WTD滤波器还存在一定的不足。
2.1.3 组合小波去噪法
经过分析WDFTD滤波器和WTD滤波器都有各自的优点和不足，所以综合两者的优点， 经两个滤波器进行组合，采用组合的小波去噪法，这样既可以滤除高频噪声，又可以很好的解决基线漂移的现象。组合小波去噪所需的matlab代码如下所示。
%%%肌电WTD+WDFTD降噪效果分析%%%
clear;
clc;
SampleFre = 2000;%采样频率
filename='/matlab.2019a/bin/paper review/sEMG数据存放/1上肢动作/1上肢动作24.csv'
P=csvread(filename,0,0);%从第1行第0列开始读取数据
[row, column]=size(P);%获取数据维度大小
sEMG=P(:,1);%获取第一个通道的肌电数据
sEMG_l=length(sEMG);%获取第一个通道的数据量
%% IWD降噪后单一评价指标的计算 %%
[XD,CXD,LXD]=wden(sEMG, 'heursure', 's', 'mln', 4, 'sym6');%对信号进行小波变换阈值
[C,L]=wavedec(XD, 5, 'sym6');%多级一维小波分解 改分解层数
ca5=appcoef(C,L,'sym6',5);%一维近似系数，计算一维信号的近似系数
[cd1,cd2,cd3,cd4,cd5]=detcoef(C,L,[1,2,3,4,5]);%一维细节系数，获取小波分解的细节系
%利用数字滤波阈值 去除基线漂移 和 高频信号降噪
%将第一层细节系数设置为0，进行高频信号降噪，将最后一层的近似系数设置为0，进行基线漂移的
C5=[zeros(size(ca5)); cd5; cd4; cd3; cd2; zeros(size(cd1))];
sEMG_wavelet=waverec(C5,L,'sym6');%多层次一维小波重构
figure(1);%Create figure window
% 展示IWD降噪后信号
subplot(2, 1, 1);
plot(sEMG_wavelet);
base_line = zeros(1,sEMG_l);
hold on;
plot(base_line, 'r');
title('时域信号','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
ylabel('幅值/V','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
% 展示IWD降噪后幅频信号
subplot(2, 1, 2);
t = (0:sEMG_l-1)/SampleFre;%频率的倒数为时间
sEMG_fft = fft(sEMG_wavelet);%对信号进行傅里叶变换，此时的数据为对称的复数，需要进行
sEMG_fft_single = 2 * abs(sEMG_fft(1:length(sEMG_fft)/2)) / length(sEMG_fft);
Frequence_single = SampleFre * (1:length(sEMG_fft)/2) / length(sEMG_fft);
plot(Frequence_single, sEMG_fft_single);
ylabel('幅值/V','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
title('频域信号','FontSize',30, 'FontWeight', 'bold');% 设置肢体大小，字体加粗
axis([0 1000 0 3*10^(-6)])
sEMG_f(1:sEMG_l-1) = sEMG(1:sEMG_l-1);%为平滑度准备数据
sEMG_b(1:sEMG_l-1) = sEMG(2:sEMG_l);
sEMG_wavelet_f(1:sEMG_l-1) = sEMG_wavelet(1:sEMG_l-1);
sEMG_wavelet_b(1:sEMG_l-1) = sEMG_wavelet(2:sEMG_l);
RMSE_IWD = sqrt(sum((sEMG-sEMG_wavelet).^2)/sEMG_l);%计算均方根误差
SNR_IWD = 10*log10((sum(sEMG_wavelet.^2)/sEMG_l)/(sum((sEMG-mean(sEMG))-sEMG_l)));
r_IWD = sum((sEMG_wavelet_b-sEMG_wavelet_f).^2)/sum((sEMG_b-sEMG_f).^2);%计算平
% 输出单个评价指标的值
fprintf('WTD的RMSE(均方根)：\t%f\n', RMSE_IWD);
fprintf('WTD的SNR(信噪比)：\t%f\n', SNR_IWD);
fprintf('WTD的r(平滑度)：\t%f\n', r_IWD);
运行代码，所得到的各个子动作sEMG信号经组合小波去噪法后的时频域图像及评价指标如下所示
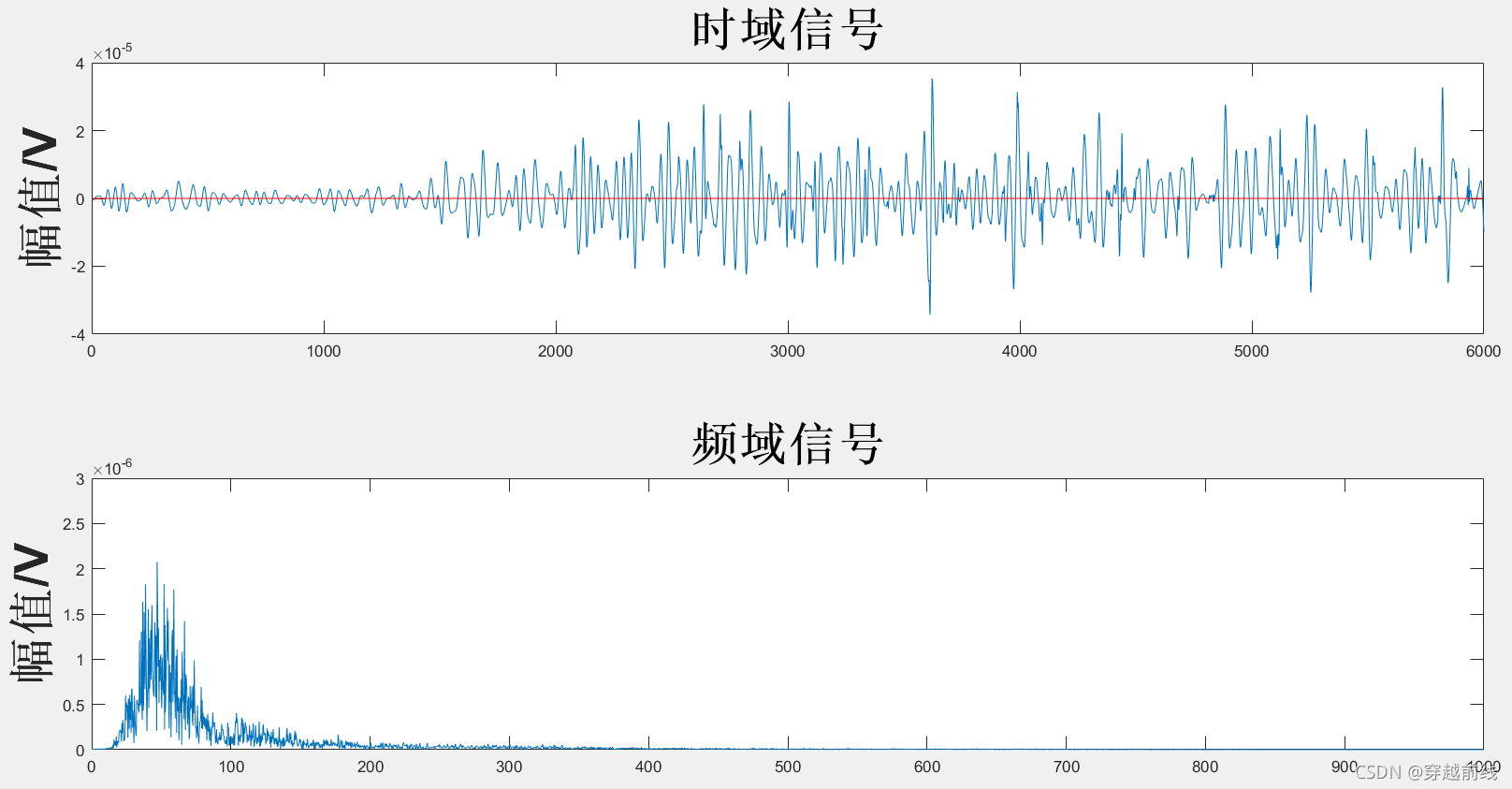
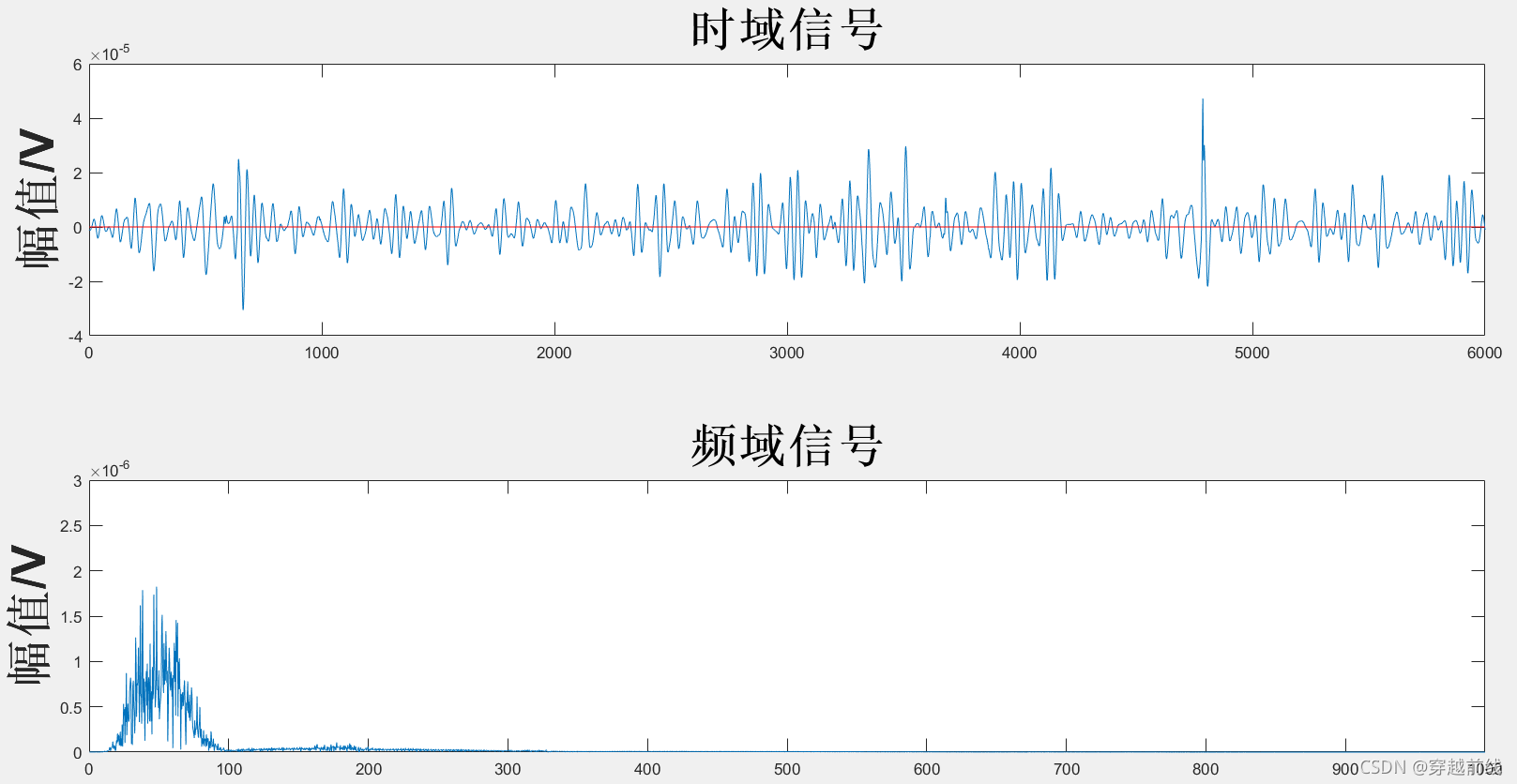
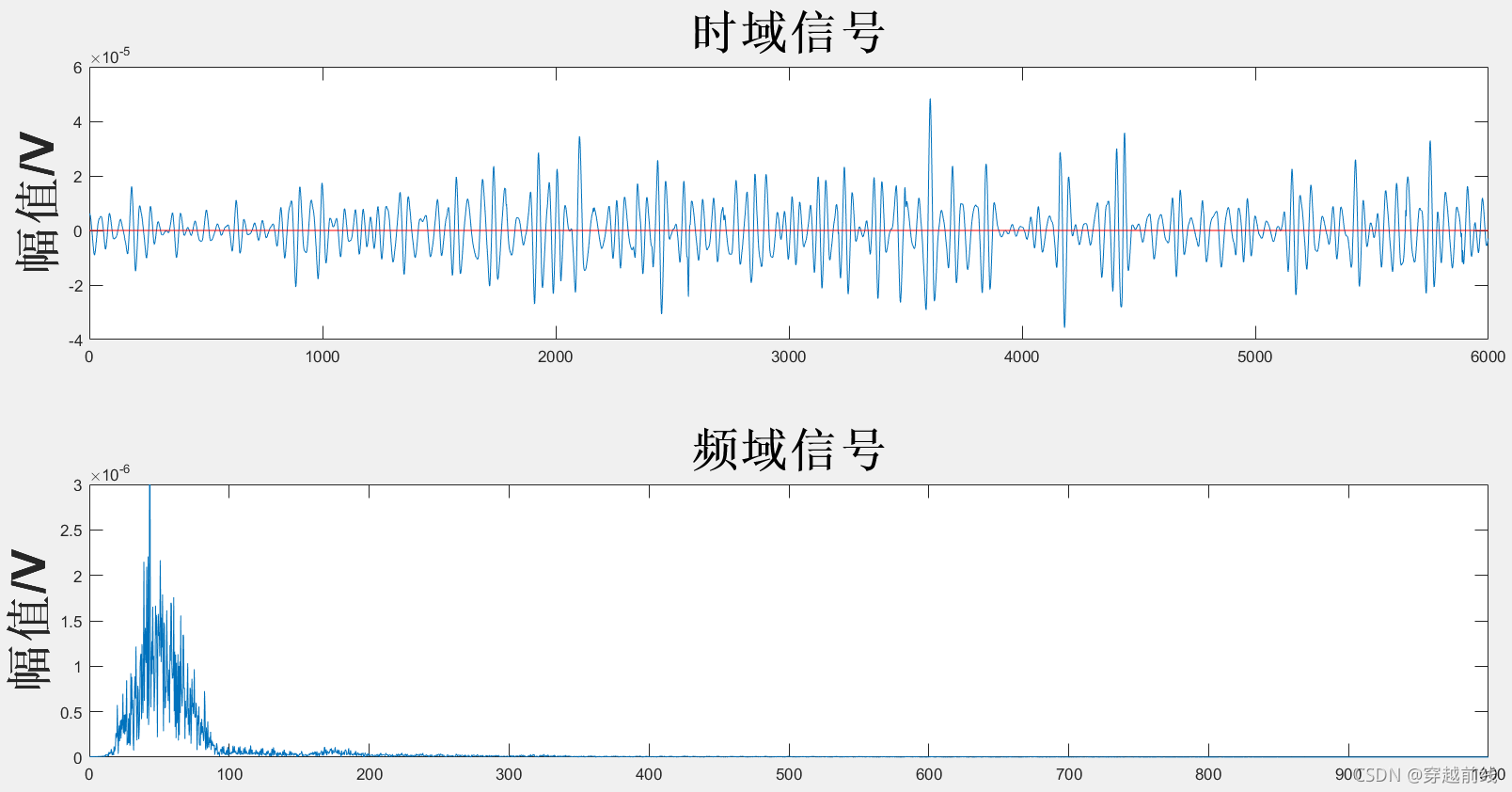
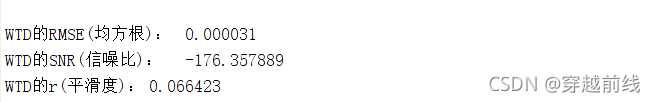
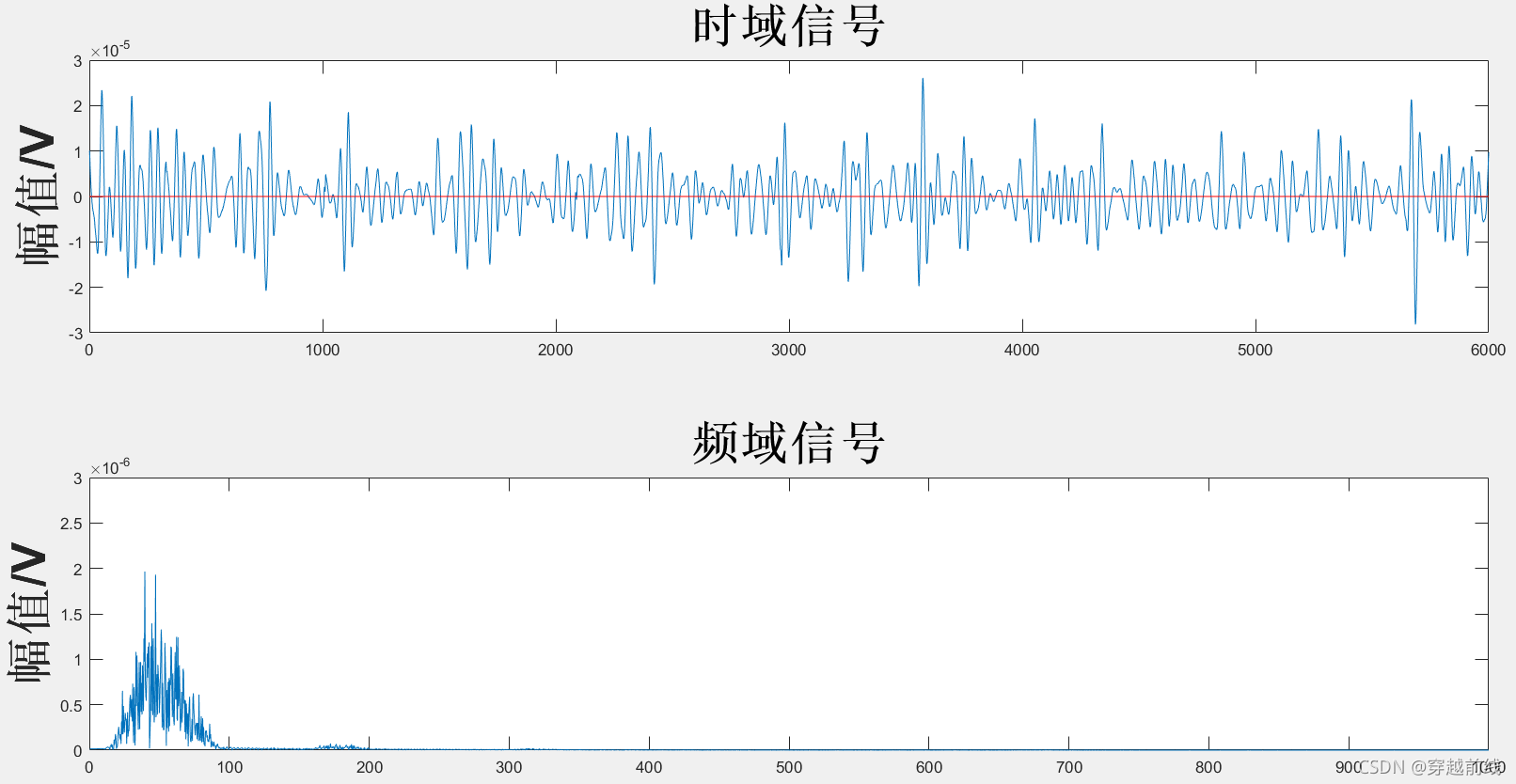
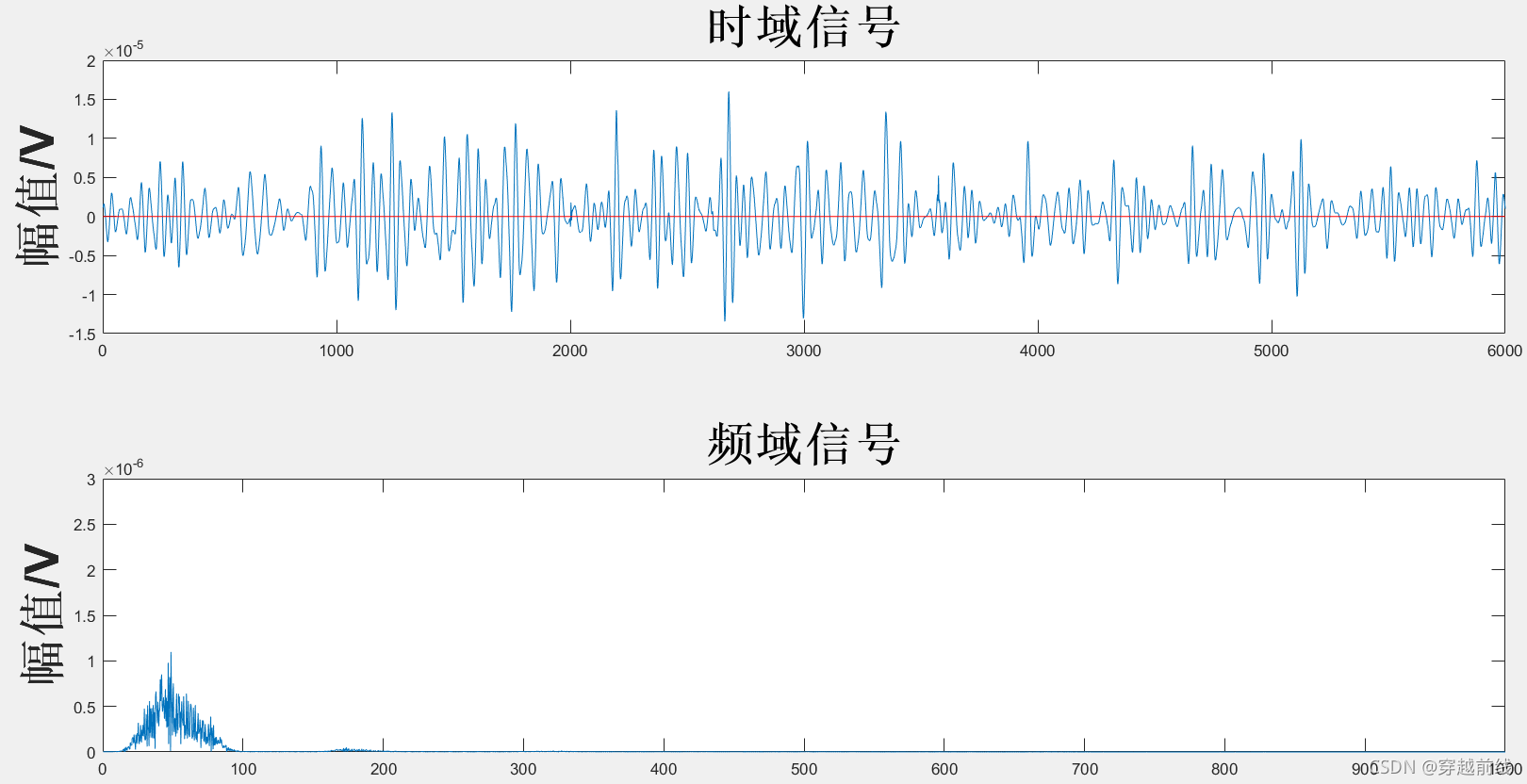
经过组合小波滤波器处理的信号具有较好的平滑度，同时信噪比也比较高， 符合信号滤波的要求，说明使用组合小波滤波法能够能到理想的结果。可以发现经过滤波不仅去除了对信号质量影响极大的基线漂移，也有效的滤除了500HZ以上的高频噪声。那么为了验证三种滤波器滤波的效果，我们需要用matlab代码生成三种滤波方式下的对比图。
所需matlab代码如下所示
%%% 肘屈曲第15组组数据的通道1经过WTD\WDFTD\IWD降噪后的对比 %%% close all;
clear;
clc;
%% 数据读取 %%
filename = '/matlab.2019a/bin/paper review/sEMG数据存放/1上肢动作/1上肢动作24.csv'
P=csvread(filename,1,0);%从第1行第0列开始读取数据
[row, column]=size(P);%获取数据维度大小
sEMG=P(:,4);%获取第一个通道的肌电数据
sEMG_l=length(sEMG);%获取第一个通道的数据量
figure(2)
% 展示原始信号
subplot(4, 1, 1);
plot(sEMG);
base_line = zeros(1,sEMG_l);
hold on;
plot(base_line, 'r'); title('原始信号');
ylabel('幅值/V');%y轴的标签
%% WTD降噪后单一评价指标的计算 %%
[XD_WTD,CXD,LXD]=wden(sEMG, 'heursure', 's', 'mln', 4, 'sym6');%对信号进行小波变
sEMG_f(1:sEMG_l-1) = sEMG(1:sEMG_l-1);%为平滑度准备数据
sEMG_b(1:sEMG_l-1) = sEMG(2:sEMG_l);
XD_f(1:sEMG_l-1) = XD_WTD(1:sEMG_l-1);
XD_b(1:sEMG_l-1) = XD_WTD(2:sEMG_l);
RMSE_WTD = sqrt(sum((sEMG-XD_WTD).^2)/sEMG_l);%计算均方根误差
SNR_WTD = 10*log10((sum(XD_WTD.^2)/sEMG_l)/(sum((sEMG-XD_WTD).^2)/sEMG_l));%计算
r_WTD = sum((XD_b-XD_f).^2)/sum((sEMG_b-sEMG_f).^2);%计算平滑度
% 将计算得到的数据放入容器
RMSE_cont(1) = RMSE_WTD;
SNR_cont(1) = SNR_WTD;
r_cont(1) = r_WTD;
% 展示WTD降噪后信号
subplot(4, 1, 2); plot(XD_WTD);
base_line = zeros(1,sEMG_l);
hold on;
plot(base_line, 'r');
title('WTD降噪');
ylabel('幅值/V');%y轴的标签
%输出单个评价指标的值
fprintf('WTD的RMSE：\t%f\n', RMSE_WTD);
fprintf('WTD 的 SNR：\t%f\n', SNR_WTD);
fprintf('WTD的r：\t%f\n', r_WTD);
fprintf('\n');
%% WDFTD降噪后单一评价指标的计算 %%
[C,L]=wavedec(sEMG,5,'sym6');%多级一维小波分解 改分解层数
ca5=appcoef(C,L,'sym6',5);%一维近似系数，计算一维信号的近似系数
[cd1,cd2,cd3,cd4,cd5]=detcoef(C,L,[1,2,3,4,5]);%一维细节系数，获取小波分解的细节系
%利用数字滤波阈值 去除基线漂移 和 高频信号降噪
%将第一层细节系数设置为0，进行高频信号降噪，将最后一层的近似系数设置为0，进行基线漂移的
C5=[zeros(size(ca5));
cd5; cd4; cd3; cd2; zeros(size(cd1))];
% C5=[ca5; cd5; cd4; cd3; cd2; zeros(size(cd1))];%没有去除基线漂移
sEMG_wavelet=waverec(C5,L,'sym6');%多层次一维小波重构
sEMG_f(1:sEMG_l-1) = sEMG(1:sEMG_l-1);%为平滑度准备数据
sEMG_b(1:sEMG_l-1) = sEMG(2:sEMG_l);
sEMG_wavelet_f(1:sEMG_l-1) = sEMG_wavelet(1:sEMG_l-1);
sEMG_wavelet_b(1:sEMG_l-1) = sEMG_wavelet(2:sEMG_l);
RMSE_WDFTD = sqrt(sum((sEMG-sEMG_wavelet).^2)/sEMG_l);%计算均方根误差
SNR_WDFTD = 10*log10((sum(sEMG_wavelet.^2)/sEMG_l)/(sum((sEMG-sEMG_wavelet).^2)))
r_WDFTD = sum((sEMG_wavelet_b-sEMG_wavelet_f).^2)/sum((sEMG_b-sEMG_f).^2);%计算
% 将计算得到的数据放入容器
RMSE_cont(2) = RMSE_WDFTD; SNR_cont(2) = SNR_WDFTD;
r_cont(2) = r_WDFTD;
% 展示WTD降噪后信号
subplot(4, 1, 3);
plot(sEMG_wavelet);
base_line = zeros(1,sEMG_l); hold on;
plot(base_line, 'r'); title('WDFTD降噪');
ylabel('幅值/V');%y轴的标签
% 输出单个评价指标的值
fprintf('WDFTD的RMSE：\t%f\n', RMSE_WDFTD);
fprintf('WDFTD 的 SNR：\t%f\n', SNR_WDFTD);
fprintf('WDFTD的r：\t%f\n', r_WDFTD);
fprintf('\n');
%% IWD降噪后单一评价指标的计算 %%
[XD,CXD,LXD]=wden(sEMG, 'heursure', 's', 'mln', 4, 'sym6');%对信号进行小波变换阈值
% [C,L]=wavedec(sEMG, 5, 'sym6');%多级一维小波分解 改分解层数
[C,L]=wavedec(XD, 5, 'sym6');%多级一维小波分解 改分解层数
ca5=appcoef(C,L,'sym6',5);%一维近似系数，计算一维信号的近似系数
[cd1,cd2,cd3,cd4,cd5]=detcoef(C,L,[1,2,3,4,5]);%一维细节系数，获取小波分解的细节系
%利用数字滤波阈值 去除基线漂移 和 高频信号降噪
%将第一层细节系数设置为0，进行高频信号降噪，将最后一层的近似系数设置为0，进行基线漂移的
C5=[zeros(size(ca5));
cd5; cd4; cd3; cd2; zeros(size(cd1))];
% C5=[ca5; cd5; cd4; cd3; cd2; zeros(size(cd1))];%没有去除基线漂移
sEMG_wavelet=waverec(C5,L,'sym6');%多层次一维小波重构
% XD=waverec(C5,L,'sym6');
%多层次一维小波重构
% [sEMG_wavelet,CXD,LXD]=wden(XD, 'heursure', 's', 'mln', 4, 'sym6');%对信号进行
%%% 上面注释掉的代码，验证了更改WDFTD和WTD的顺序，对去噪效果有无影响，经验证，无影响！
sEMG_f(1:sEMG_l-1) = sEMG(1:sEMG_l-1);%为平滑度准备数据sEMG_b(1:sEMG_l-1) = sEMG(2:sEMG_l);
sEMG_wavelet_f(1:sEMG_l-1) = sEMG_wavelet(1:sEMG_l-1);
sEMG_wavelet_b(1:sEMG_l-1) = sEMG_wavelet(2:sEMG_l);
RMSE_IWD = sqrt(sum((sEMG-sEMG_wavelet).^2)/sEMG_l);%计算均方根误差
SNR_IWD = 10*log10((sum(sEMG_wavelet.^2)/sEMG_l)/(sum((sEMG-sEMG_wavelet).^2)))/sEMG_l
r_IWD = sum((sEMG_wavelet_b-sEMG_wavelet_f).^2)/sum((sEMG_b-sEMG_f).^2);%计算平
% 将计算得到的数据放入容器
RMSE_cont(3) = RMSE_IWD; SNR_cont(3) = SNR_IWD; r_cont(3) = r_IWD;
% 展示IWD降噪后信号
subplot(4, 1, 4);
plot(sEMG_wavelet);
base_line = zeros(1,sEMG_l);
hold on;
plot(base_line, 'r');
title('IWD降噪');
ylabel('幅值/V');%y轴的标签
% 输出单个评价指标的值
fprintf('IWD的RMSE：\t%f\n', RMSE_IWD);
fprintf('IWD 的 SNR：\t%f\n', SNR_IWD);
fprintf('IWD的r：\t%f\n', r_IWD);
%% 评价指标归一化和综合评价指标的计算 %%
%评价指标的归一化
PRMSE = (RMSE_cont-min(RMSE_cont))/(max(RMSE_cont)-min(RMSE_cont));%均方根误差的
PSNR = (SNR_cont-min(SNR_cont))/(max(SNR_cont)-min(SNR_cont));%信噪比的归一化处理
Pr = (r_cont-min(r_cont))/(max(r_cont)-min(r_cont));%平滑度的归一化处理
%综合评价值T的计算
PRMSE_mean = mean(PRMSE);%计算均方根误差的均值
Pr_mean = mean(Pr);%计算平滑度的均值
PRMSE_std = std(PRMSE);%计算均方根误差的标准差
Pr_std = std(Pr);%计算平滑度的标准差
PRMSE_CV = PRMSE_std/PRMSE_mean;%计算均方根误差的变异系数
Pr_CV = Pr_std/Pr_mean;%计算平滑度的变异系数
PRMSE_W = PRMSE_CV/(PRMSE_CV+Pr_CV);%计算均方根误差的权重
Pr_W = Pr_CV/(PRMSE_CV+Pr_CV);%计算平滑度的权重
T = PRMSE_W*PRMSE + Pr_W*Pr;%计算综合指标T
%综合评价值P的计算
PSNR_mean = mean(PSNR);%计算信噪比的均值
PSNR_std = std(PSNR);%计算信噪比的方差
PSNR_CV = PSNR_std/PSNR_mean;%计算信噪比的变异系数
PRMSE_W_P = PRMSE_CV/(PRMSE_CV+Pr_CV+PSNR_CV);%计算均方根误差的权重,P评价指标
PSNR_W_P = PSNR_CV/(PRMSE_CV+Pr_CV+PSNR_CV);%计算信噪比的权重,P评价指标
Pr_W_P = Pr_CV/(PRMSE_CV+Pr_CV+PSNR_CV);%计算平滑度的权重,P评价指标
P = PRMSE_W_P*PRMSE - PSNR_W_P*PSNR + Pr_W_P*Pr + T;%计算综合评价指标P
%% 绘图 %%
figure(1)
subplot(2, 1, 1);
T=plot(T,':h','LineWidth',3); hold on;
P=plot(P,'-.h','LineWidth',3);
xlabel('分解层数','FontSize',20,'FontWeight','bold');
ylabel('归一化值','FontSize',20,'FontWeight','bold');
legend([T, P], 'T', 'P');%添加图例
subplot(2, 1, 2);
RMSE=plot(RMSE_cont, '-o');
hold on;
SNR=plot(SNR_cont, '-o');
hold on;
r=plot(r_cont, '-o');
legend([RMSE, SNR, r], 'RMSE', 'SNR', 'r');%添加图例
%% end
通过运行此程序，可以将原始信号，小波变换阈值去噪（WTD）后的信号和基于小波变换数字滤波阈值去噪（WDFTD）以及混合小波变换后的信号展现到一张图中，让我们更轻松地看出几种信号的差异，以此来分析出哪种滤波更合适。如下图所示。
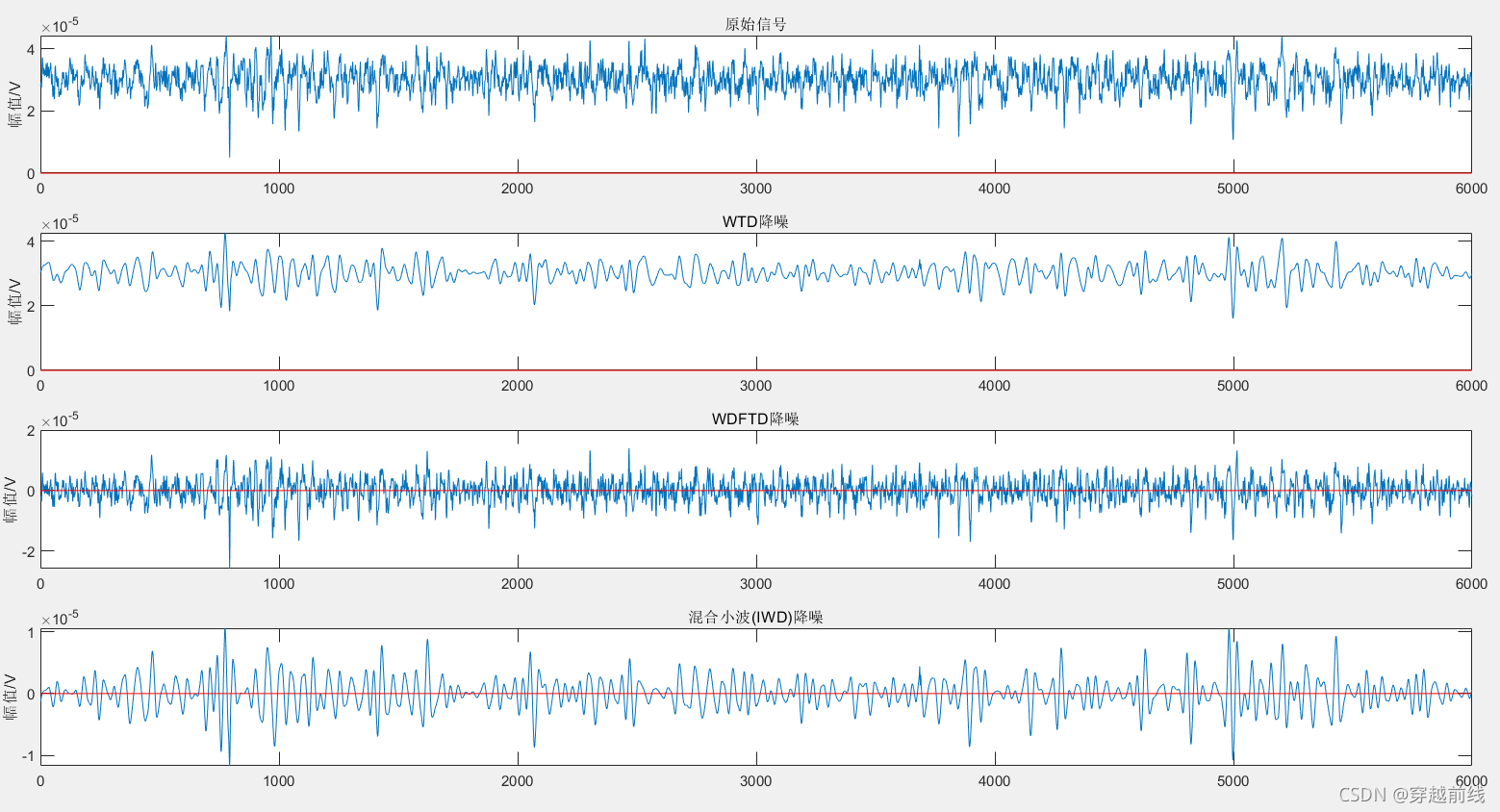
在此只展现了Act1子动作下各种滤波信号的比较。经过比较，可以发现组合小波滤波器处理的信号具有较好的平滑度，同时信噪比也比较高， 符合信号滤波的要求，说明使用组合小波滤波法能够能到理想的结果。并且经过组合小波滤波不仅去除了对信号质量影响极大的基线漂移，也有效的滤除了500HZ以上的高频噪声，相较于其他的几种滤波，组合小波变换的效果更加理想。
2.2 脑电信号预处理
2.2.1 FIR滤波器
数字FIR滤波器是指有限脉冲响应的数字滤波器，它是数字信号处理领域中使用较多的的一种滤波器，FIR数字滤波器具有有限长度的脉冲采样响应特性，比较稳定。因此， FIR滤波器使用的场景要比IIR滤波器多，其在信息传输、信号处理以及图像滤波等领域都具有广泛的应用。IIR数字滤波器具有模拟滤波器的一些比较好的特性，如良好的振幅和频率特性，但其相位不是线性的。FIR滤波器有以下特点：
- 系统的单位冲激响应h(n)在有限个n值处不为零；
- 系统函数H(z)在∣z∣ > 0处收敛，并只有零点；
- 结构上没有输出到输入的反馈。
2.2.2 脑电带通滤波
本文首先采用了肌电信号的处理方式，对脑电信号进行了高频噪声的去除和基线漂移的去除，降噪后的结果如下图所示，通过处理后的时域图可以看到，信号去除基线漂移后失去了时域上的特征，这是因为再去除基线漂移的过程中对信号进行了小波重构，这使得信号出现了图中的情况，即时域信号趋于平缓，上下起伏不明显，这将影响后续的动作识别工作，所以经过考虑放弃了此方案。
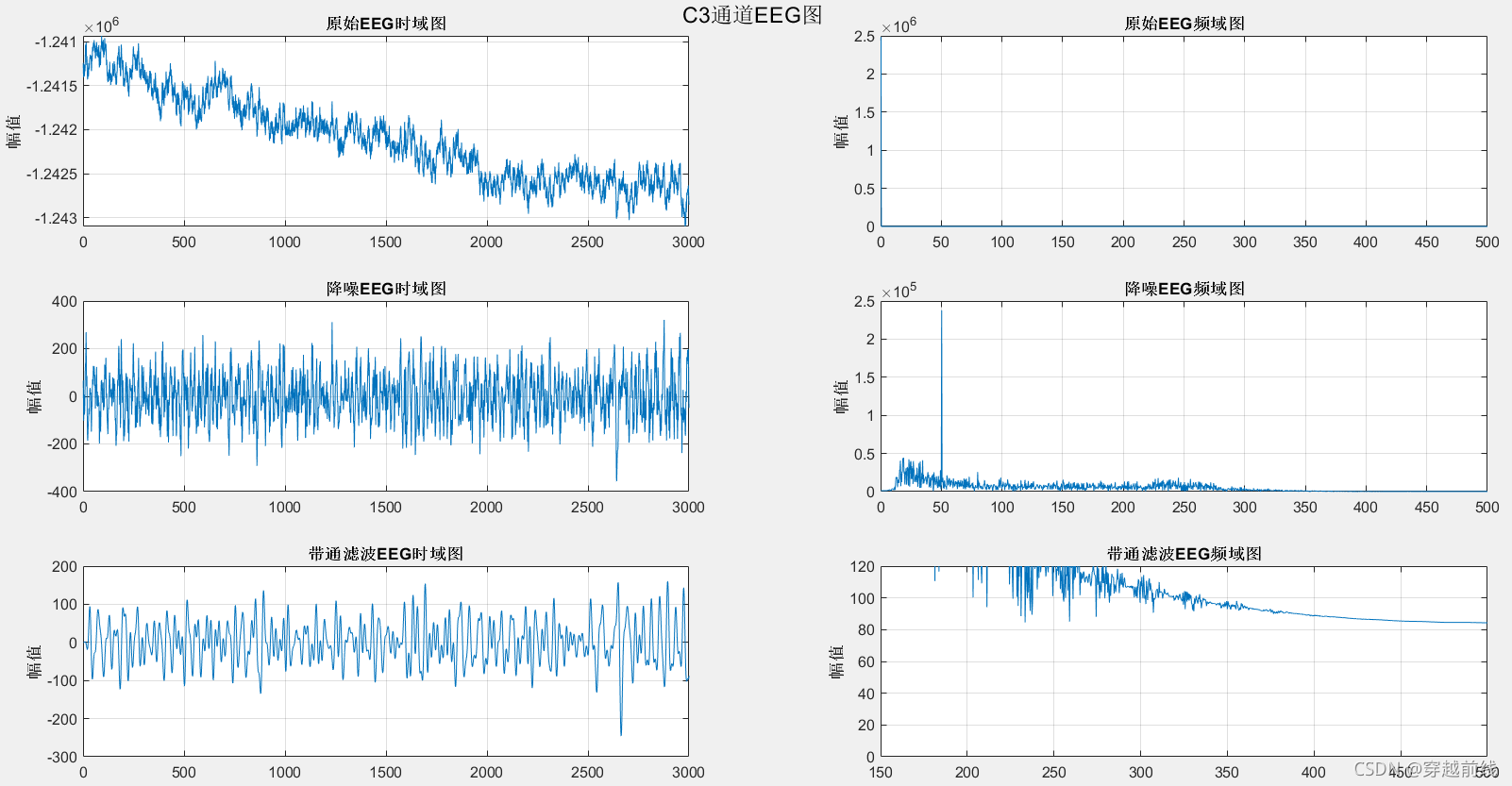
实现小波重构进行带通滤波所需要的代码如下所示。
%%%对EEG信号进行小波去基线，并带通滤波%%%
clear;
clc;
filename='/matlab.2019a/bin/paper review/EEG数据存放/1上肢动作/1上肢动作25.csv';%从第1行第0列开始读取数据
P=csvread(filename);%从第1行第0列开始读取数据
SampleFre = 1000;%采样频率
EEG=P(:,5);%获取一个通道的肌电数据
EEG_l=length(EEG);%获取一个通道的数据量
%% 去除基线和高频噪声
% [EEG,CXD,LXD]=wden(EEG, 'heursure', 's', 'mln', 3, 'sym6');%对信号进行小波变换阈
[C,L]=wavedec(EEG,5,'sym6');%多级一维小波分解 改分解层数
ca5=appcoef(C,L,'sym6',5);%一维近似系数，计算一维信号的近似系数
[cd1,cd2,cd3,cd4,cd5]=detcoef(C,L,[1,2,3,4,5]);%一维细节系数，获取小波分解的细节系
%利用数字滤波阈值 去除基线漂移 和 高频信号降噪
%将第一层细节系数设置为0，进行高频信号降噪，将最后一层的近似系数设置为0，进行基线漂移的
C5=[zeros(size(ca5)); cd5; cd4;
cd3; cd2; zeros(size(cd1))];
% C5=[ca5; cd5; cd4; cd3; cd2; zeros(size(cd1))];
EEG_wavelet=waverec(C5,L,'sym6');%多层次一维小波重构
t = (0:EEG_l-1)/SampleFre;%频率的倒数为时间
EEG_fft = fft(EEG);%对原始信号进行傅里叶变换
EEG_fft_single = 2 * abs(EEG_fft(1:length(EEG_fft)/2)) / length(EEG_fft);
Frequence_single = SampleFre * (1:length(EEG_fft)/2) / length(EEG_fft);
EEG_wavelet_fft = fft(EEG_wavelet);%对处理后的信号进行傅里叶变换
EEG_wavelet_fft_single = 2 * abs(EEG_wavelet_fft(1:length(EEG_wavelet_fft)/2));
Frequence_single_wavelet = SampleFre * (1:length(EEG_wavelet_fft)/2) / length(EEG_fft);
%% 带通滤波
% 滤波器长度
N=41;
%滤波器的特征频率
fp_bandpass=[5 40];% 带通
%以采样频率的一半，对频率归一化
wn_bandpass=fp_bandpass * 2/SampleFre;
%采用fir1函数设计FIR滤波器
b_bandpass=fir1(N-1,wn_bandpass,'bandpass');% 带通
%进行带通滤波，返回滤波后的信号
EEG_bandpass_sig=filter(b_bandpass,1,EEG_wavelet);
EEG_bandpass_fft = fft(EEG_bandpass_sig);%对处理后的信号进行傅里叶变换
EEG_bandpass_fft_single = 2 * abs(EEG_bandpass_fft(1:length(EEG_bandpass_fft)/2));
Frequence_single_wavelet = SampleFre * (1:length(EEG_bandpass_fft)/2) / length(EEG_bandpass_fft);
%% 绘图
figure(1);%Create figure window
%%% 原始信号的时域和频域图
suptitle('C3通道EEG图');
subplot(3,2,1);
plot(EEG);%原始信号
grid;
title('原始EEG时域图','FontWeight','bold');
ylabel('幅值','FontWeight','bold');
subplot(3,2,2);
plot(Frequence_single,EEG_fft_single);%原始信号频谱图
grid;
title('原始EEG频域图','FontWeight','bold');
ylabel('幅值','FontWeight','bold');
% ylim([0,20]);
%%% 去基线信号的时域和频域图
subplot(3,2,3);
plot(EEG_wavelet);%重构信号
grid;
title('降噪EEG时域图','FontWeight','bold');
ylabel('幅值','FontWeight','bold');
subplot(3,2,4);
plot(Frequence_single_wavelet,EEG_wavelet_fft_single);%重构信号频谱图
grid;
title('降噪EEG频域图','FontWeight','bold');
ylabel('幅值','FontWeight','bold');
subplot(3,2,5);
plot(EEG_bandpass_sig);%带通滤波信号
grid;
title('带通滤波EEG时域图','FontWeight','bold');
ylabel('幅值','FontWeight','bold');
subplot(3,2,6);
plot(Frequence_single_wavelet,EEG_bandpass_fft_single);%带通滤波信号频谱图
grid;
title('带通滤波EEG频域图','FontWeight','bold');
ylabel('幅值','FontWeight','bold');
ylim([0,120]);
扫一扫
1037
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
