字典树的实际应用场景之敏感词过滤（附 Java 实现代码）

前言

这篇文章主要介绍怎么用字典树实现敏感词的过滤，关于字典树的一些介绍可以参考其他文章，也看一下我的另一篇文章：Trie（字典树，前缀树）及其实现；

敏感词过滤

在很多场景都会用到敏感词过滤，比如在网站提交的内容，游戏中的聊天等等…那么这些敏感词是如何被过滤掉的呢？其实这就是一个字符串的匹配过程，我们很容易就可以想到的就是准备一个敏感词库，然后用每一个敏感词去要过滤的文本中匹配，匹配成功则用 *** 来代替敏感词，不同的匹配算法的时间复杂度是不一样的，比如敏感词的长度为m，待过滤文本的长度为 n，有如下几种匹配算法：

• 暴力破解法，利用两层循环来实现，时间复杂度为O(m * n);
• KMP算法：时间复杂度为 O(n + m)；
• 字典树：时间复杂度为O(n)；

Trie 实现敏感词的过滤

关于 KMP 算法的实现可以参考其他文章或者我的另外两篇文章：字符串模式匹配算法的 Java 实现 和 关于 KMP 算法的个人理解(附 Java 实现代码)

首先，在进行敏感词过滤之前我们需要有一个敏感词库，用这个敏感词库来建立字典树，比如我们现在有两个敏感词：“de”, “bca”，建立字典树，根节点不存放任何东西，其他每个子节点存放一个字符，深红色代表单词结尾，如下：

建立完字典树之后，我们就要利用这棵由敏感词组成的字典树匹配字符串了。

现在，我们有一段文本 “abcadef" ，目的是将其中的 “de”, “bca”,过滤掉，具体算法如下：

• 为了遍历字符串和字典树，我们假设有三个指针，p1,p2,p3，其中p1指向字典树根节点，p2 和 p3 指向字符串的第一个字符，如下：

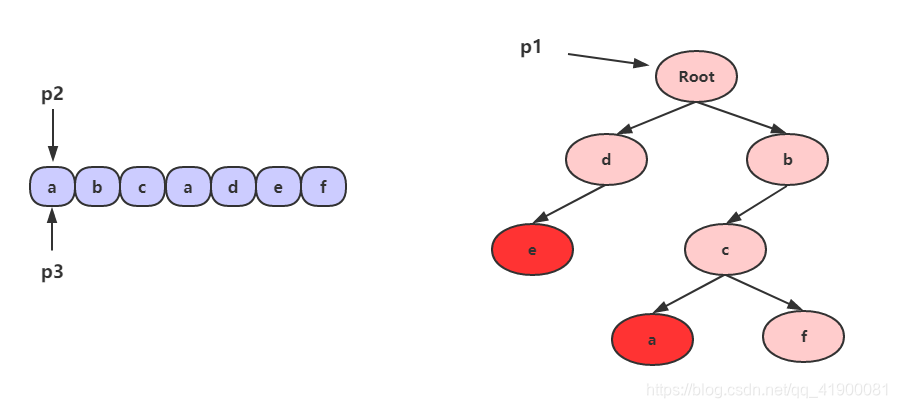
• 然后从字符串的 a 开始，检测有没有以 a 作为前缀的敏感词，直接判断 p1 的孩子节点中是否有 a 这个节点就可以了，显然这里没有。接着把指针 p2 和 p3 向右移动一格。

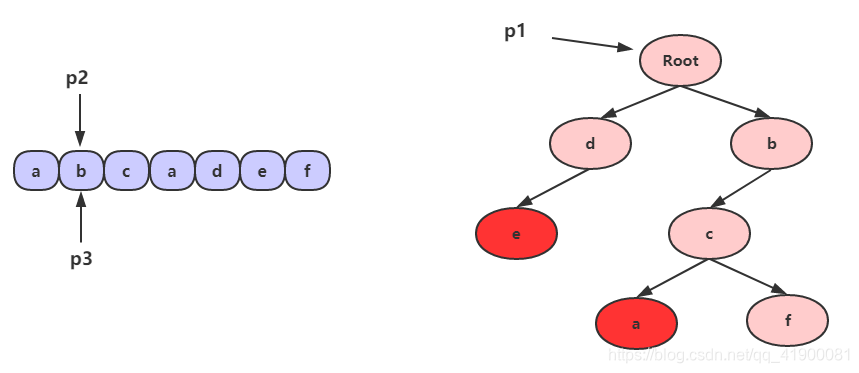
• 然后从字符串 b 开始查找，看看是否有以 b 作为前缀的字符串，p1 的孩子节点中有 b，这时，我们把 p1 指向节点 b，由于此时 b 不是单词的结尾，所以p3 向右移动一格，不过，p2 不动。
  
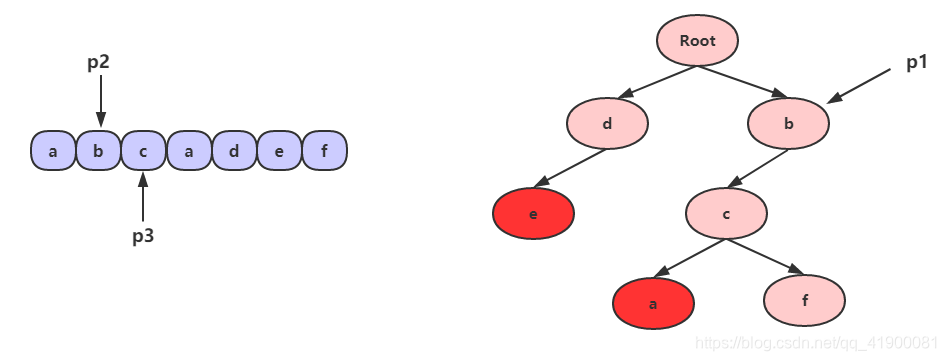
• 判断 p1 的孩子节点中是否存在 p3 指向的字符 c，显然有。我们把 p1 指向节点 c，p3 向右移动一格，p2 不动。
  
• 判断 p1 的孩子节点中是否存在 p3 指向的字符 a，显然有，且 a 是字符串 “bca” 的结尾。这意味着，p2 到 p3之间为敏感词 “bca”，把 p2 和 p3 指向的区间那些字符替换成 *。这时我们把 p2 和 p3 都移向字符 d，p1 还是还原到最开始指向 root。

• 和前面的步骤一样，判断有没以 d 作为前缀的字符串，显然这里有 “de”，所以把 p2 和 p3 移到字符 f。

• 因为根节点没有子节点 f，所以匹配结束。

在 Java 中可以利用 HashMap 来存放一层树结点，则每个敏感词的查找时间复杂度是 O (1)，字符串的长度为 n，我们需要遍历 1 遍，所以敏感词查找这个过程的时间复杂度是 O (n * 1)。如果每个敏感词的平均长度为 m，有 t 个敏感词的话，构建 trie 树的时间复杂度是 O (t * m)。

但在实际的应用中，构建 trie 树的时间复杂度可以忽略，因为 trie 树我们可以在一开始就构建了，以后可以无数次重复利用的了。

Java 代码实现

import org.apache.commons.lang.CharUtils;
import java.util.HashMap;
import java.util.Map;

public class MyTrie {
   
    private class TrieNode {
   
        /**
         * 是否敏感词的结尾
         */
        private boolean isEnd = false;

        /**
         * 下一层节点
         */
        Map<Character, TrieNode>