知识点 - 几何模板解析几何版

最新推荐文章于 2024-03-31 15:51:24 发布

Best KeyBoard

最新推荐文章于 2024-03-31 15:51:24 发布

阅读量274

点赞数

CC 4.0 BY-SA版权

分类专栏：数学-计算几何

本文链接：https://blog.youkuaiyun.com/qq_41848675/article/details/99697833

数学-计算几何专栏收录该内容

7 篇文章

订阅专栏

本文深入探讨了计算几何中直线与线段交点的解析几何方法，包括直线交点的求解公式、线段交点的判断算法及线性变换原理。同时，详细介绍了圆线交、圆圆交及圆圆切线的计算方法，提供了丰富的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

知识点 - 计算几何方程（解析几何）版

直线交，线段交

$A x + B y + C = 0 .$ 可以由两个点的得到 $P_x , P_y , Q_x , Q_y$ .
$A = P_y - Q_y,B = Q_x - P_x,C = - A P_x - B P_y.$
联立方程
$\begin{cases} a_1 x + b_1 y + c_1 = 0 \\\\ a_2 x + b_2 y + c_2 = 0 \end{cases}\\$
解得
$\frac{\begin{vmatrix}c_1 & b_1 \cr c_2 & b_2\end{vmatrix}}{\begin{vmatrix}a_1 & b_1 \cr a_2 & b_2\end{vmatrix} } = - \frac{c_1 b_2 - c_2 b_1}{a_1 b_2 - a_2 b_1},\\ y = - \frac{\begin{vmatrix}a_1 & c_1 \cr a_2 & c_2\end{vmatrix}}{\begin{vmatrix}a_1 & b_1 \cr a_2 & b_2\end{vmatrix}} = - \frac{a_1 c_2 - a_2 c_1}{a_1 b_2 - a_2 b_1}.$

struct pt {
    double x, y;

    bool operator<(const pt& p) const
    {
        return x < p.x - EPS || (abs(x - p.x) < EPS && y < p.y - EPS);
    }
};

struct line {
    double a, b, c;

    line() {}
    line(pt p, pt q)
    {
        a = p.y - q.y;
        b = q.x - p.x;
        c = -a * p.x - b * p.y;
        norm();
    }

    void norm()
    {
        double z = sqrt(a * a + b * b);
        if (abs(z) > EPS)
            a /= z, b /= z, c /= z;
    }

    double dist(pt p) const { return a * p.x + b * p.y + c; }
};

const double EPS = 1e-9;

double det(double a, double b, double c, double d) {
    return a*d - b*c;
}
//直线交
bool intersect(line m, line n, pt & res) {
    double zn = det(m.a, m.b, n.a, n.b);
    if (abs(zn) < EPS)
        return false;
    res.x = -det(m.c, m.b, n.c, n.b) / zn;
    res.y = -det(m.a, m.c, n.a, n.c) / zn;
    return true;
}

bool parallel(line m, line n) {
    return abs(det(m.a, m.b, n.a, n.b)) < EPS;
}

bool equivalent(line m, line n) {
    return abs(det(m.a, m.b, n.a, n.b)) < EPS
        && abs(det(m.a, m.c, n.a, n.c)) < EPS
        && abs(det(m.b, m.c, n.b, n.c)) < EPS;
}

//线段交
inline bool betw(double l, double r, double x)
{
    return min(l, r) <= x + EPS && x <= max(l, r) + EPS;
}

inline bool intersect_1d(double a, double b, double c, double d)
{
    if (a > b)
        swap(a, b);
    if (c > d)
        swap(c, d);
    return max(a, c) <= min(b, d) + EPS;
}

bool intersect(pt a, pt b, pt c, pt d, pt& left, pt& right)
{
    if (!intersect_1d(a.x, b.x, c.x, d.x) || !intersect_1d(a.y, b.y, c.y, d.y))
        return false;
    line m(a, b);
    line n(c, d);
    double zn = det(m.a, m.b, n.a, n.b);
    if (abs(zn) < EPS) {
        if (abs(m.dist(c)) > EPS || abs(n.dist(a)) > EPS)
            return false;
        if (b < a)
            swap(a, b);
        if (d < c)
            swap(c, d);
        left = max(a, c);
        right = min(b, d);
        return true;
    } else {
        left.x = right.x = -det(m.c, m.b, n.c, n.b) / zn;
        left.y = right.y = -det(m.a, m.c, n.a, n.c) / zn;
        return betw(a.x, b.x, left.x) && betw(a.y, b.y, left.y) &&
               betw(c.x, d.x, left.x) && betw(c.y, d.y, left.y);
    }
}

附带判断是否线段相交,用叉乘版

struct pt {
    long long x, y;
    pt() {}
    pt(long long _x, long long _y) : x(_x), y(_y) {}
    pt operator-(const pt& p) const { return pt(x - p.x, y - p.y); }
    long long cross(const pt& p) const { return x * p.y - y * p.x; }
    long long cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
};

int sgn(const long long& x) { return x >= 0 ? x ? 1 : 0 : -1; }

bool inter1(long long a, long long b, long long c, long long d) {
    if (a > b)
        swap(a, b);
    if (c > d)
        swap(c, d);
    return max(a, c) <= min(b, d);
}

bool check_inter(const pt& a, const pt& b, const pt& c, const pt& d) {
    if (c.cross(a, d) == 0 && c.cross(b, d) == 0)
        return inter1(a.x, b.x, c.x, d.x) && inter1(a.y, b.y, c.y, d.y);
    return sgn(a.cross(b, c)) != sgn(a.cross(b, d)) &&
           sgn(c.cross(d, a)) != sgn(c.cross(d, b));
}

线性变换

如何将一个点(x1,y1)变换（旋转，平移，反射，投影，伸缩，切变）到另一个点(x2,y2)？你首先要知道3个点变换前后的坐标，然后列方程：
$(x1,y1)->(x2,y2)\\ x2=A1\cdot x1+B1\cdot y1+C1\\ y2=A2\cdot x1+B2\cdot y1+C2$

六个方程即可解出
高斯消元，用分数保证精度

圆线交

不妨设圆心在原点,(若不是这样，可以移动坐标系)
$\because d_0 = \frac{|C|}{\sqrt{A^2+B^2}} \\ \therefore x_0 = - \frac{AC}{A^2 + B^2} \\ y_0 = - \frac{BC}{A^2 + B^2} \\又\because d = \sqrt{r^2 - \frac{C^2}{A^2 + B^2}} ,令 m = \sqrt{\frac{d^2}{A^2 + B^2}} \\ \therefore a_x = x_0 + B \cdot m, a_y = y_0 - A \cdot m\\ b_x = x_0 - B \cdot m, b_y = y_0 + A \cdot m$

double r, a, b, c; // given as input
double x0 = -a*c/(a*a+b*b), y0 = -b*c/(a*a+b*b);
if (c*c > r*r*(a*a+b*b)+EPS)
    puts ("no points");
else if (abs (c*c - r*r*(a*a+b*b)) < EPS) {
    puts ("1 point");
    cout << x0 << ' ' << y0 << '\n';
}
else {
    double d = r*r - c*c/(a*a+b*b);
    double mult = sqrt (d / (a*a+b*b));
    double ax, ay, bx, by;
    ax = x0 + b * mult;
    bx = x0 - b * mult;
    ay = y0 - a * mult;
    by = y0 + a * mult;
    puts ("2 points");
    cout << ax << ' ' << ay << '\n' << bx << ' ' << by << '\n';
}

圆圆交

不妨设一个圆心在原点
$x^2+y^2=r_1^2\\ (x - x_2)^2 + (y - y_2)^2 = r_2^2$
连立得到
$\cdot (-2x_2) + y \cdot (-2y_2) + (x_2^2+y_2^2+r_1^2-r_2^2) = 0$
变成了圆线交。

圆圆切线

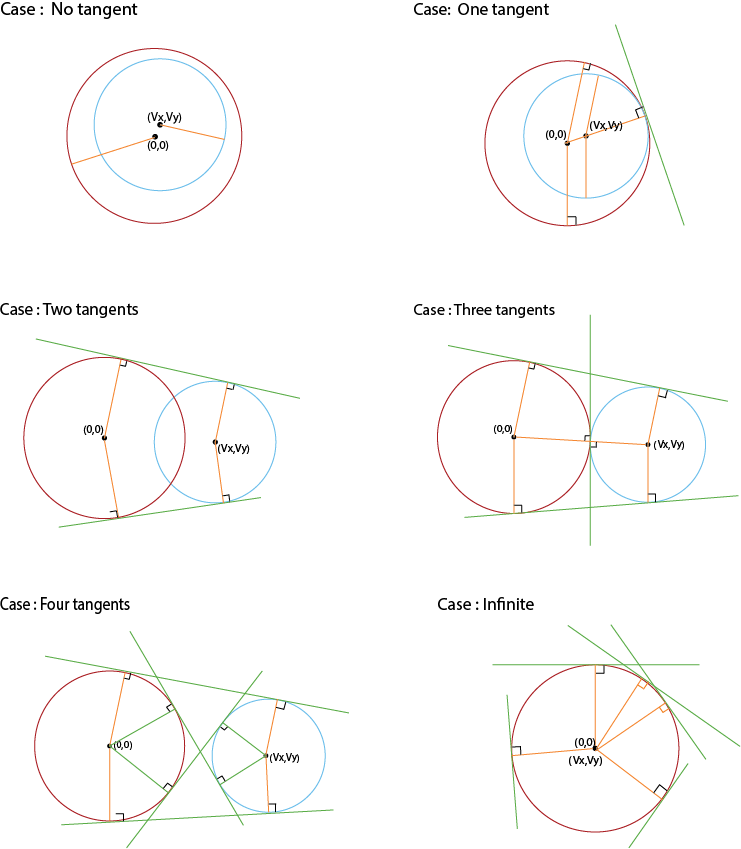
不妨设一个圆心在原点。问题转化为一条直线到 $v_1$ 距离 $r_1$ , $v_2$ 距离 $r_2$ .另外我们让 $A^2+B^2=1$ 这样保证直线只有一种形式，并且化简了点到直线公式。于是得到：
$a^2 + b^2 = 1\\\mid a \cdot 0 + b \cdot 0 + c \mid = r_1\\\mid a \cdot v_x + b \cdot v_y + c \mid = r_2$
拆绝对值，令 $d1=±r1,d2=±r2d_1 = \pm r_1,d_2 = \pm r_2$
$d_2 - d_1 ) v_x \pm v_y \sqrt{v_x^2 + v_y^2-(d_2-d_1)^2} \over {v_x^2 + v_y^2} }\\ b = {( d_2 - d_1 ) v_y \pm v_x \sqrt{v_x^2 + v_y^2-(d_2-d_1)^2} \over {v_x^2 + v_y^2} }\\ c = d_1$
移回去的方法是 $\cdot x_0 + b \cdot y_0$

double sqr (double a) {
    return a * a;
}
void tangents (pt c, double r1, double r2, vector<line> & ans) {
    double r = r2 - r1;
    double z = sqr(c.x) + sqr(c.y);
    double d = z - sqr(r);
    if (d < -EPS)  return;
    d = sqrt (abs (d));
    line l;
    l.a = (c.x * r + c.y * d) / z;
    l.b = (c.y * r - c.x * d) / z;
    l.c = r1;
    ans.push_back (l);
}

vector<line> tangents (circle a, circle b) {
    vector<line> ans;
    for (int i=-1; i<=1; i+=2)
        for (int j=-1; j<=1; j+=2)
            tangents (b-a, a.r*i, b.r*j, ans);
    for (size_t i=0; i<ans.size(); ++i)
        ans[i].c -= ans[i].a * a.x + ans[i].b * a.y;
    return ans;
}

线段并

统计直线上的线段并总长

int length_union(const vector<pair<int, int>> &a) {
    int n = a.size();
    vector<pair<int, bool>> x(n*2);
    for (int i = 0; i < n; i++) {
        x[i*2] = {a[i].first, false};
        x[i*2+1] = {a[i].second, true};
    }

    sort(x.begin(), x.end());

    int result = 0;
    int c = 0;
    for (int i = 0; i < n * 2; i++) {
        if (i > 0 && x[i].first > x[i-1].first && c > 0)
            result += x[i].first - x[i-1].first;
        if (x[i].second)
            c--;
        else
            c++;
    }
    return result;
}