一、拓扑排序概述
一场大型工程,我们往往把它看做多个子工程的集合体,这些小工程有的相互连接,一个是一个的子工程,有的相互并列,共处于一个工程的顺序之下,我们可以画一个图来表示这个工程和这些子工程的联系,它称为AOV网。
举个例子:小S作为班级的学习委员,掌管全班的收发作业,他手下还有一些班干部,但是作业实在太多了,而且人手有限,不可能同时收发所有科目作业,所以,他决定权衡利弊,优先收脾气不好的老师所布置的作业,先给他送过去,比如脾气特别暴躁的物理老头,假如作业不能及时送过去,不免一番批评。数学,物理,生物都是重要的科目,这三科可以分散班委同时收。小S和英语老师关系不错,所以可以暂缓。而语文老师比较人性,偶尔皮一下也可以过关。所以这项工程画成AOV网如下表示:
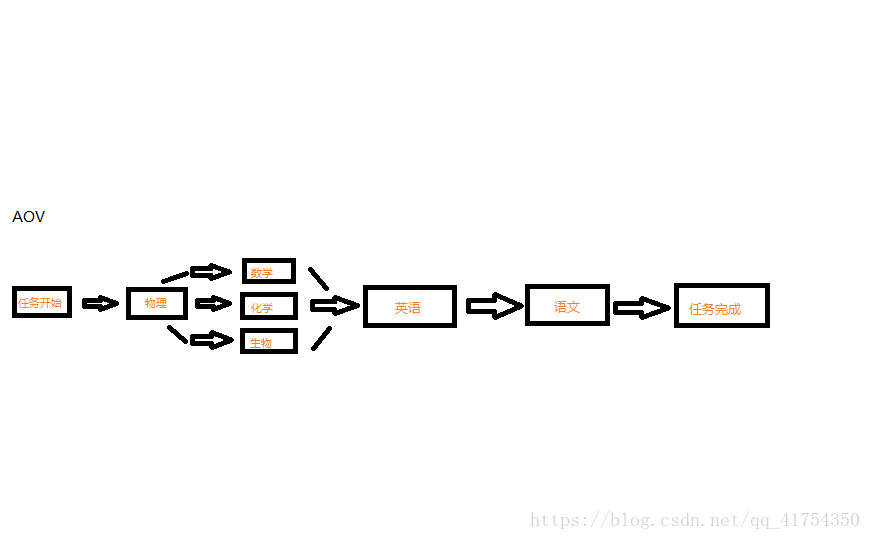
拓扑排序是一个AOV网中的重要算法,只应用于有向无环图(这十分重要!!!)
假如说不是一个有向无环图,这与理论和事实都是相悖的。举个例子,收英语作业的前提是数学、化学和生物都收完了,而收语文的前提是英语作业收完,假如说语文是数学、化学和生物的前提,这就会产生逻辑上的混乱,现实工程也会难以实现。
构造拓扑排序列可以帮助我们合理安排一个工程的进度,而由AOV网构造拓扑排序非常便捷,且有很高的使用价值。
二、拓扑排序算法
对于AOV的子工程来说来说,每一个节点都拥有入度(有多少点导向它,也就是开始它有多少前提)和出度(它导向多少点,也就是它是多少工程开始的前提)。例如 英语 的入度为3,出度为1。
拓扑排序的算法思想非常简单:
1)我们逐个找出一个入度为0的顶点并输出。
2)然后删除它自己以及和它相邻的程序边。
3)重复上方两部,直到找不出入度为零的点。
4)若输出的顶点数小于总顶点数,那说明这个图有回路,否则它就是一个拓扑序列。
为了实现以上思路,我们会引入一个栈进行操作,我们现在模拟一下:
1、开始时只有任务开始入度为0,将开始入栈【栈:开始】。{拓扑序列:空}
2、栈顶元素出栈并输出(开始的后继工程物理的入度减一,相当于删除开始的相临边)【栈:空】。{拓扑序列:开始}
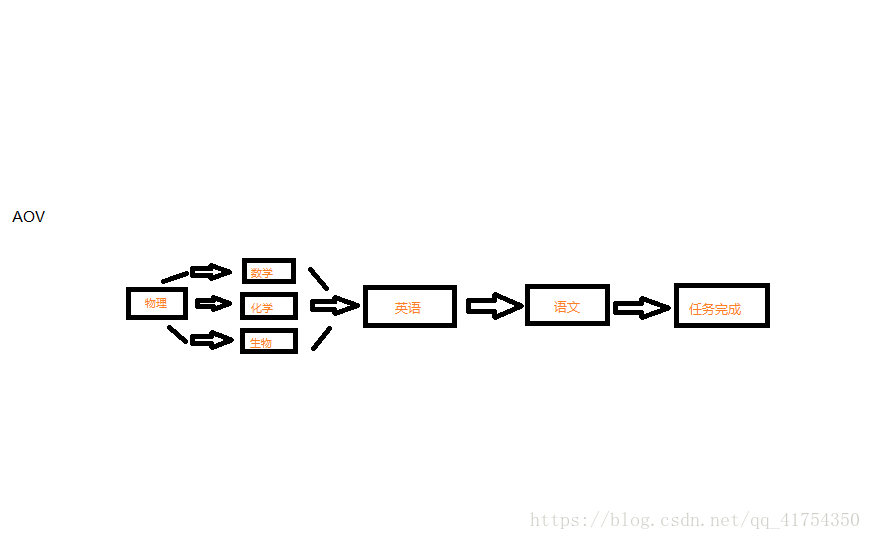
3、物理的入度为0将物理入栈 【栈:物理】。{拓扑序列:开始}
4、栈顶元素物理出栈并输出(开始的后继工程数学、化学和生物的入度减一,相当于删除物理的相临边)【栈:空】。{拓扑序列:开始、物理}
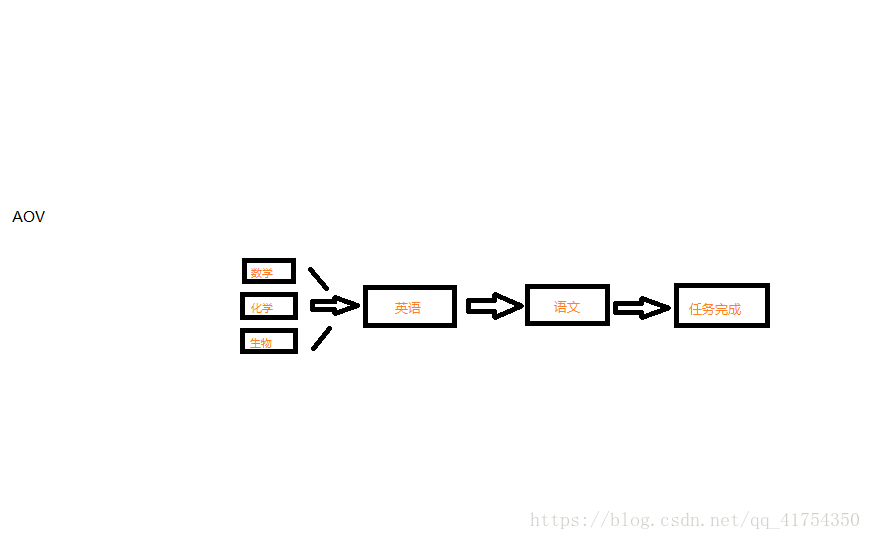
5、这三科的入度都为0,依次入栈(顺序不唯一,看它自己的顺序了,比如:开始为第一个子工程,物理是第二个,数学我把它视为第三个,化学第四,生物第五)【栈:数学、化学、生物】。{拓扑序列:开始、物理}
6、栈顶元素生物出栈并输出,它的后继英语入度减一 【栈:数学、化学】;栈顶元素化学出栈并输出,它的后继英语入度减一 【栈:数学】;栈顶元素数学出栈,后继英语入度减一 【栈:空】{拓扑序列:开始、物理、生物、化学、数学}
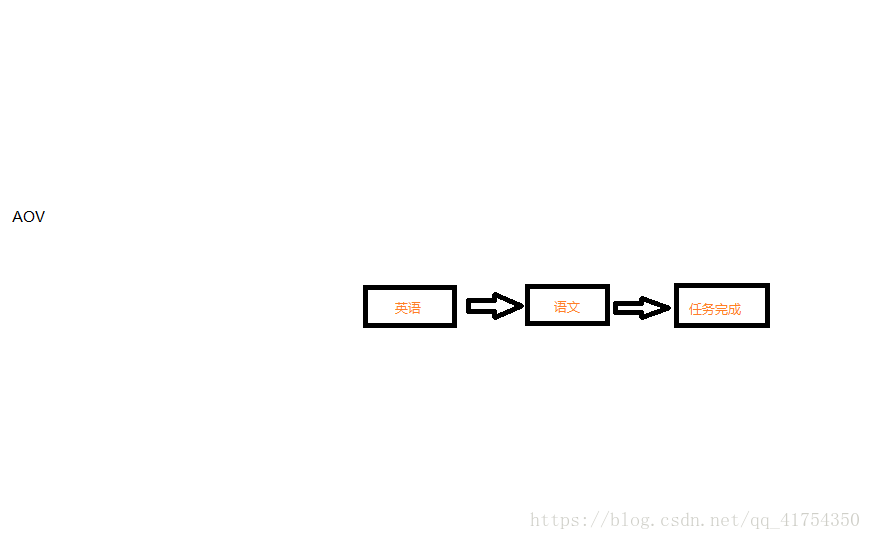
7、此时英语入度为0并将其入栈【栈:英语】 {拓扑序列:开始、物理、生物、化学、数学}
8、出栈并输出栈顶元素英语,后继语文入度减一【栈:空】 {拓扑序列:开始、物理、生物、化学、数学、英语}
9、语文入栈并输出,完成入度减一【栈:空】 {拓扑序列:开始、物理、生物、化学、数学、英语、语文}
10、完成入栈、输出并出栈【栈:空】 {拓扑序列:开始、物理、生物、化学、数学、英语、语文、完成}
这就是上图模拟的过程。
三、代码展示
实现主要靠以下步骤:
1)数据结构需要存储每个点的入度ru[ ],出度chu[ ],第几个点对应的数值a[这个点][第几个出度]=?,栈stack[ ]。
2)初始化:int top=0。
3)for 循环查找入度为0的点。
4)将其入栈。
5)拓扑排序计数器 count=0。
6)while 栈非空 (top>0)
<1>栈顶元素k出栈;--top;输出它;++count。
<2>for k后每个后继点p
【1】ru[p]--;(p的入度减一)
【2】if ru【p】==0 顶点p入栈。
上面的叙述已经很详细了,本次不贴代码,请小伙伴们加油理解!
另外后续章节关键路径是AOV网的重要知识点,点击便可以继续学习。
https://blog.youkuaiyun.com/qq_41754350/article/details/81025658





 本文介绍了拓扑排序的概念,它应用于有向无环图(AOV网)。通过一个生动的例子解释了如何进行拓扑排序,包括算法思想和具体步骤。拓扑排序算法通过寻找入度为0的节点并输出,逐步构建排序序列,如果排序序列少于总节点数则说明图有回路。此外,文章还提到了后续章节的关键路径知识。
本文介绍了拓扑排序的概念,它应用于有向无环图(AOV网)。通过一个生动的例子解释了如何进行拓扑排序,包括算法思想和具体步骤。拓扑排序算法通过寻找入度为0的节点并输出,逐步构建排序序列,如果排序序列少于总节点数则说明图有回路。此外,文章还提到了后续章节的关键路径知识。
















 1488
1488

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








