基础计算几何（叉积）

 图来源于网络。

基本思路

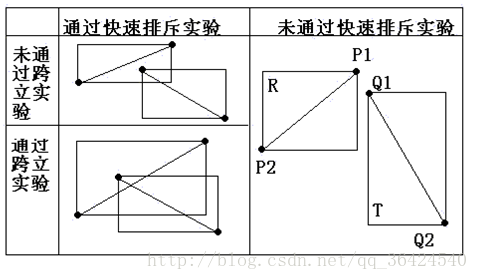
① 快速排斥实验（不涉及计算几何）：如果两条边所在矩形不相交则一定不相交，即满足

（min(x1,x2)<=max(x3,x4) &&

min(x3,x4)<=max(x1,x2) &&

min(y1,y2)<=max(y3,y4) &&

min(y3,y4)<=max(y1,y2)） 才可能相交

②跨立实验：即以其中一条线段为直线，判断另一线段的两端点是否在它两边，

但是可能出现以下情况：

 

所以要判断两次，即两条线段都要为直线，判断另一线段的两端点是否在它两边

若是则两线段相交

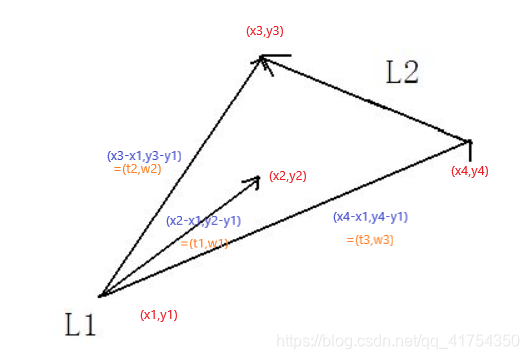
跨立实验可用叉积来解决：

设这四个点为x1,y1,x2,y2，x3,y3,x4,y4

L1的坐标为t1=x1-x2,w1=y1-y2，

1端点到3,4的线段向量分别为t2=x1-x3,w2=y1-y3,t3=x1-x4,w3=y1-y4；

则3,4在L1两端即为(t1*w2-t2*w1)*(t1*w3-t3*w1)<=0  (叉积公式 x1*y2-x2*y1)

（叉积可以辨别方向，选取端点1的向量为向量1，再选端点3、4为向