模拟退火算法

最新推荐文章于 2024-01-04 14:22:37 发布

Toniht

最新推荐文章于 2024-01-04 14:22:37 发布

阅读量349

点赞数

CC 4.0 BY-SA版权

分类专栏：知识点

本文链接：https://blog.youkuaiyun.com/qq_41746268/article/details/90639872

知识点专栏收录该内容

49 篇文章

订阅专栏

本文介绍模拟退火算法，它是一种随机求取最优解的算法，改进了爬山算法可能停在局部最优的弊端。若下一状态为更优解则跳转，非更优解也有一定概率跳转，随温度降低该概率下降。作者对确定初始温度和衰减值存疑，还给出最小包含球代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

模拟退火算法

具体解释就不详细说了，这里有大佬的博客
https://www.cnblogs.com/ranjiewen/p/6084052.html
https://blog.youkuaiyun.com/acdreamers/article/details/10019849

只想说自己的理解。
首先来讲模拟退火是一种随机算法，它是一种求取最优解的算法。改进了爬山算法可能会停在局部最优的弊端。
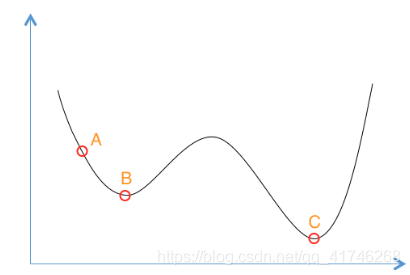
在这里插入图片描述
（截自大佬博客的图）
拿这个举例，爬山算法从Ａ开始寻找，往右寻找因为Ｂ处于局部最优而导致停止，而我们需要的最优解为Ｃ点。于是模拟退火改进为如果下一状态为更优解，我们就跳到下一状态，如果下一状态不是更优解，我们以一定概率跳到下一状态。这样就会有概率跳到B点的右边，最后选择最优解Ｃ点。
下面这是来自wiki的动态解释
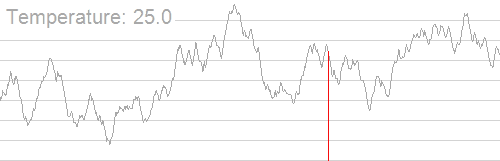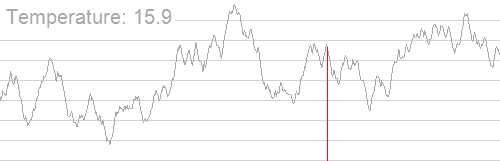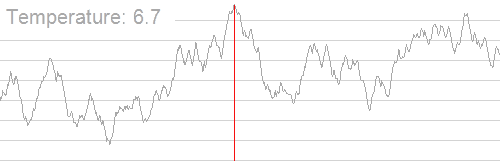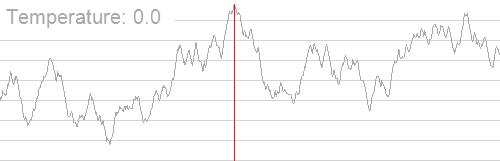
在这里插入图片描述
随着温度降低，跳到非更优解的概率明显降低，也正因为如此整个答案才会逐渐趋近最优解。

我弄不太明白的就是决定这个求取最优解的概率，因为它是由初始温度Ｔ和衰减值delta控制的，在做题时如何确定这个初始温度和衰减值来确定能求出最优解（太菜了只能在TLE的边缘疯狂试探），否则即便写出程序也很有可能是WA,因为毕竟是个随机算法

一份最小包含球的代码
http://poj.org/problem?id=2069
找一个最小球的半径将给出的所有点包含在内

 
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <cmath>
#include <string>
#include <cstring>
#include <map>
#include <set>
#include <cmath>
//#include <tr1/unordered_map>
//#include <bits/stdc++.h>

using namespace std;
#define me(x,y) memset(x,y,sizeof x)
#define MIN(x,y) x < y ? x : y
#define MAX(x,y) x > y ? x : y
typedef long long ll;
typedef unsigned long long ull;
const double INF = 0x3f3f3f3f;
const double eps = 1e-08;
const double PI = acos(-1.0);
const double T=100;
const double delta=0.98;
const int maxn = 55;

struct Point{
	double x,y,z;
	double dis(Point A){
		return sqrt((A.x-x)*(A.x-x)+(A.y-y)*(A.y-y)+(A.z-z)*(A.z-z));
	}
};
double search(Point p[],int n){
	Point s = p[0];
	double t=T;
	double ans=INF;
	while(t > eps){
		int k = 0;
		for(int i = 0; i < n; ++i){
			if(s.dis(p[i]) > s.dis(p[k])) k = i;
		}
		double d = s.dis(p[k]);
		ans = min(ans,d);
		s.x += (p[k].x - s.x)/d*t;
		s.y += (p[k].y - s.y)/d*t;
		s.z += (p[k].z - s.z)/d*t;
		t *= delta;
	}
	return ans;
}
Point p[maxn];
int main(){
	int n;
	while(cin>>n && n){
		for(int i = 0; i < n; ++i){
			scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].z);
		}
		printf("%.5f\n",search(p,n));
	}
	return 0;
}

 
/*
 
 
*/