汉诺塔问题 -- 递归算法

hanoi塔问题描述：

  设a、b、c是3个塔座。开始时a塔座一共有n个圆盘，这些圆盘自下而上，由大到小地叠放在一起，各圆盘从大到小编号为1，2，3......n，要求将塔座a上地这一叠圆盘移到b上，并仍按同样地顺序叠置。在移动圆盘时应遵守以下移动规则：

1. 每次只能移动一个圆盘
2. 任何时刻都不允许将较大的圆盘压在较小的圆盘之上
3. 在满足移动规则1和2的前提下，可将圆盘移置a b c任一塔座。

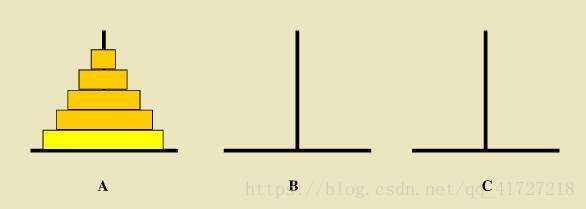
思路：

    步骤1：将n-1个较小的圆盘按原来的叠放方式从a移动到c

    步骤2：将a塔剩下的最大的盘移动到b

    步骤3：将c塔中的圆盘叠放方式不变的移动到b

代码：

• 将数组类比为a、b、c塔
• 数组中元素大小比作圆盘大小

# include <stdio.h>

void move(int *a, int *b)
{
	int temp = *a;
	*a = *b;
	*b = temp;
}

void hanoi(int n, int *arr, int *brr, int *crr)
{
	if (n > 0)
	{
		hanoi(n - 1, arr, crr, brr);
		move(&arr[n], &brr[n]);
		hanoi(n - 1, crr, brr, arr);
	}
}
int main()
{
	int arr[5] = { 0, 1, 2, 3, 4 };
	int brr[5] = { 0 };
	int crr[5] = { 0 };

	hanoi(5, arr, brr, crr);

	for (int i = 0; i < 5; i++)
	{
		printf("%d   ", arr[i]);
	}
	printf("\n");
	for (int i = 0; i < 5; i++)
	{
		printf("%d   ", brr[i]);
	}
	return 0;
}