递归原来可以so easy|-连载（4）-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_41717874/article/details/84306757

对递归进行优化–记忆化

递归可以很方便的解决很多问题，让程序变得很简洁。

但是，在递归解决问题的过程成，有时候会有很多重复计算,使得计算量很大，耗时很长。

比如，使用递归求斐波那契数列。

如果用普通的递归来解，当n值很大时，时间会很长而超时。

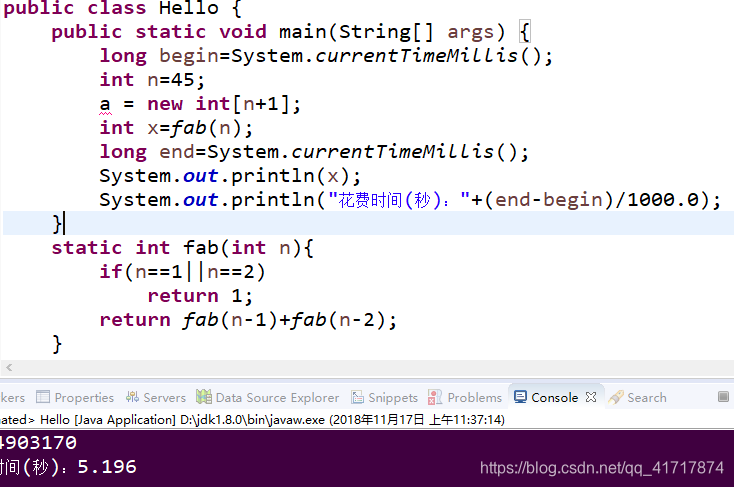
在这里插入图片描述

如图，当n等于45时，需要运行5秒才能求出结果。

分析一下，会是什么原因导致需要计算这么长时间呢？

根据斐波那契数列的递推公式：

fn=f(n-1)+f(n-2)

f(n-1)=f(n-2)+f(n-3)
f(n-2)=f(n-3)+f(n-4);
以上3行合并一下：
fn=( f(n-2)+f(n-3) ) + ( f(n-3)+f(n-4) )

可以看到， f(n-3)被重复计算了。

再看一下斐波那契数列的运行时图：

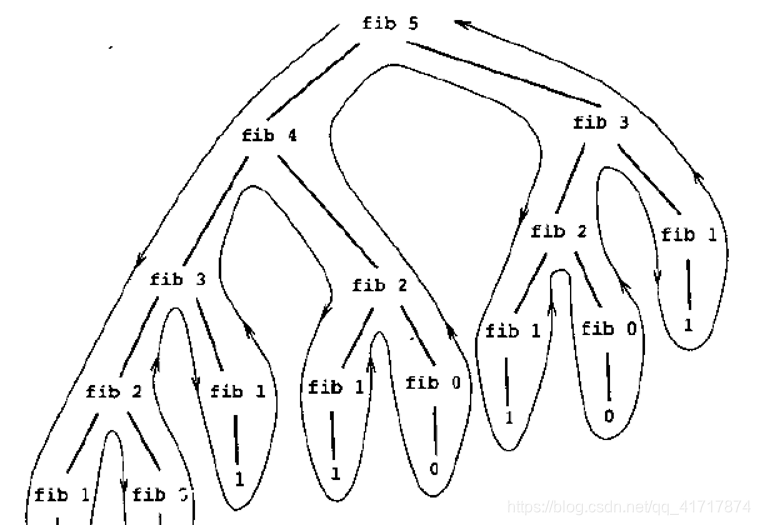
在这里插入图片描述

可以看到，有大量的重复计算。

有没有什么办法可以优化呢？

如果我们能记录一些状态的中间结果，在需要的时候直接读取结果，就可以减少重复计算。

这个思想叫着记忆化。

对于斐波那契数列，我们可以把计算完 n=2,n=3时…的值保存在数组中，下次需要使用他们来计算其他n值时，从数组中取出来，而不去再计算。

按照这个思想，代码修改为：
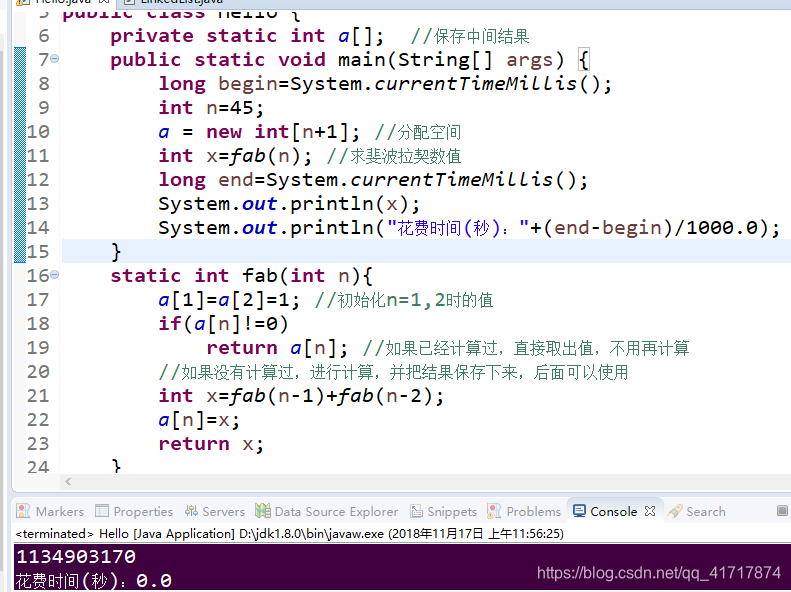
在这里插入图片描述

可以看到，经过记忆化优化后的程序，运行速度快了很多。

下面我们再看个例子。

数字三角形问题

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
如上图所示，第一行有一个数字5，表示数字三角形共有5层。

后面5行为各层的数字,组成一个数字三角形。

给出一个三角形，从三角形的顶点，只能走左下方或者右下方，然后把所遍历的数字加起来，求出最大的值。
比如对于上图来说，答案就是30(7+3+8+7+5)。

现给定一个任意的数字三角形，输出最大的值。

我们从顶点(也就是第一行第一列)开始走，其最大值为顶点的值加上从他下面两个数开始，走到底边的最大值中，更大的那个，由此，我们把问题分解成求第一行的数字到底边的最大值，到求第二行的数字到底边的最大值，这就形成了递归。
而递归的终止条件是到了最后一行，其值就是它本身。
递归的代码如下：

package test;

import java.util.Scanner;

public class Hello {
	static int d[][] = new int[100][100]; // 最多100层
	static int n;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		n = sc.nextInt(); // 总共有几层
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= i; j++)
				d[i][j] = sc.nextInt();
		int m = MaxSum(1, 1);
		System.out.println("最大值："+m);
	}

	static int MaxSum(int l, int r) {
		if (l == n)
			return d[l][r];
		else
			return Math.max(MaxSum(l + 1, r), MaxSum(l + 1, r + 1)) + d[l][r];
	}

}

样例输入输出：

输入：

6
2
96 30
83 52 60
21 65 44 61
8 79 50 41 21
61 41 50 38 79 10

输出
375

如果通过记忆化进行优化呢？

思考一下…

…

public class Hello {
	static int d[][] = new int[100][100]; // 最多100层
	static int max[][]= new int[100][100]; //保存记忆
	static int n;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		n = sc.nextInt(); // 总共有几层
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= i; j++)
				d[i][j] = sc.nextInt();
		int m = MaxSum(1, 1);
		System.out.println("最大值："+m);
	}

	static int MaxSum(int l, int r) {
		if (l == n)
			return d[l][r];
		else {
			if(max[l][r]!=0) {
				return max[l][r];
			}else {
				int x=Math.max(MaxSum(l + 1, r), MaxSum(l + 1, r + 1)) + d[l][r];
				max[l][r]=x;
				return x;				
			}
		}
	}
}