HDU 6662 Acesrc and Travel 详解（树形dp+换根）2019 暑假杭电多校

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6662

题目大意：

        每个点有两个权值是两个人的满意度,小A先来，小B后，两人交替行走，两人都想自己的差距和对方最大，问最大是多少。

题目思路：

1. 前言

       （本篇题解就相当于做一个对标程的一个详细的解释吧，可以理解这种换根思想，然后可以比赛前看一下这篇博客）

2. 做题前的思考（入手点）

        因为小A先手，细细想一下可以发现，对于小A选的每一个点，其实路径是定了的，（当小A选定一个点后，对于这个点一定有个小B最满意的点，那么小B肯定跳过去，接下来小A肯定又有一个满意的点。。。如此下去发现对于一个点来说，只要小A决定在这里下，那么结局就已经定了）

3. 考虑定起点情况

          接下来我们考虑一下如果小A的先手点定了的话，如何求这个点的最大差距。肯定要随便选一个点进行树形dp求解，我们此处选择1号点dfs，怎么转移呢，我们定义这个点的权值为（小A满意度 - 小B满意度），小A先手，所以他肯定会选择一个这个dp值最大的，而小B希望这个dp值最小。小A先手所以决定权在小A手上。当小A决定在1号点下手后，小B肯定会选择邻接点中，这个dp值最小的对吧。

        此时发现对于一个点既要记录最小dp值（小A转移需要）又要记录最大dp值（小B转移需要）。所以我们暂且定义两个数组dp1[i]，dp2[i] ，分别表示从i这个点到子树中的某个叶子节点这条链：

       dp1【i】：小B已经在 i 点了，接下来改小A走了，这种情况下的最大值（因为现在该A走了，一定会选择大的，所以是最大值）

       dp2【i】：小A已经在 i 点了，接下来改小B走了，这种情况下的最小值（因为现在该B走了，一定会选择小的，所以是最小值）

        这里的最大最小值要搞清楚。

       那么转移就是，dp1【i】=max( dp2【j】+val【i】)         ,    dp2 [ i ] = min  ( dp1 [ j ]  + val [ i ] );

       可能细心的读者发现了，代码中不仅记录了最大最小值，还有次大和次小值，接下来会解释。

4.考虑不定起点情况

          既然已经有定起点（1号点）的情况了，怎么A不以1号点做起点的情况呢？

          首先想到的是每个节点做根，重新dp一下，但是时间顶不住。

          此时要就是本题的核心了----------------------换根。

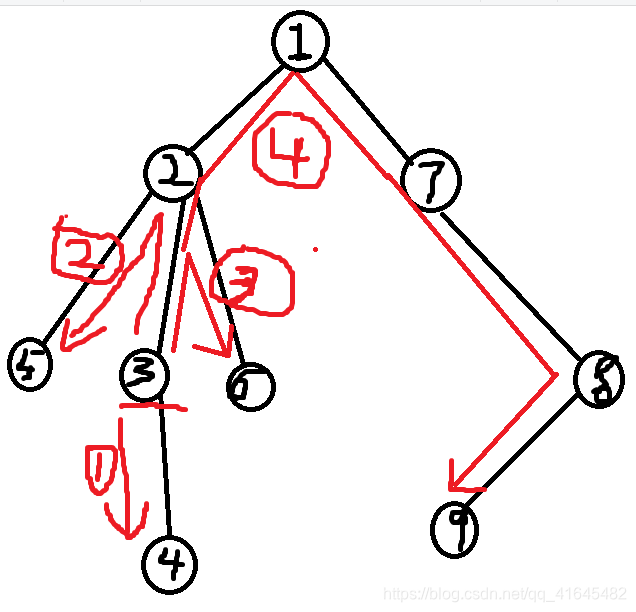
           在这幅图中可以看出3号节点向下方向的已经通过上边的树形dp得到了，如果A选择这里的最大值也就是dp2【3】

          如果考虑3做根，也就是说要考虑除了红色表明的一号路径外的红色2，3，4号路径，我们可以再做一个树形dp来解决这个，3的父亲是2号点，那么可以记录一个up1，意思同上述的dp2，但是唯一不同的是，dp2是该点到子树的叶子节点的，也就是往下走的，而我们这个up1是用来记录向上走的也就是2 -> 1 -> 7 -> 8的，如果我们直接dp1【1】的话是不是不妥呢，因为万一dp1【1】记录的正好是往下走2号点的这条路径呢，所以为了矛盾，我们要记录次大值。同理up 2和dp 1对应，也是相同的道理，p 2 记录次小值。

（up数组和dp数组，地位同等，只是方向不同）

（up数组和dp数组，地位同等，只是方向不同）

 （up数组和dp数组，地位同等，只是方向不同）

          但是此时还有一点不妥，为啥呢？我们考虑完红色4号路了，也考虑红色一号路了，2，3号路怎么办呢，所以3向上的路径还有走兄弟的这种可能，所以up2【2】还要记录dp 2 的一个最大值，如果最小值正好走的是3号节点所在的路径，那么要换次大值 ，所以一个点的up数组更新要考虑两部分。

         1. 父亲的父亲（2的父亲是1号点）父亲的up值

         2. 兄弟  （没有兄弟就不用考虑，也就是代码中的d【u】==1的情况）（5，6是3的兄弟）父亲的dp值，并判断是不是走的这条链，如果是就换次值  。

                                        

5. 计算答案

         如何计算答案呢，假如小A选择了三号点，那么小B一定会选择往上还是往下，也就是选择走dp还是选择走up，中最小的那个，所以我们枚举每个点，取向上的最小也就是up1，再取向下的最小也就是dp2。

         如果是叶子节点的话，只能往上走，所以此时的dp2【i】是个无效的状态，就算是个很大的值也没有价值，因为在叶子节点小B没有选择dp这个选项，只能选择up。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll MAXN = 2e5+5;
const ll inf = 1e16;
ll dp1[MAXN][3],dp2[MAXN][3];
ll a[MAXN],d[MAXN];
ll n;
vector<ll>v[MAXN];

void dfs(ll fa,ll u)
{
    ll len=v[u].size();
    for(ll i=0;i<len;i++){
        ll to = v[u][i];
        if(to == fa)continue;
        dfs(u,to),d[u]++;
        if(dp1[u][1] < dp2[to][1] + a[u])dp1[u][2] = dp1[u][1] , dp1[u][1] = dp2[to][1] + a[u];
        else if(dp1[u][2] < dp2[to][1] + a[u])dp1[u][2] = dp2[to][1] + a[u];

        if(dp2[u][1] > dp1[to][1] + a[u])dp2[u][2]=dp2[u][1] , dp2[u][1] = dp1[to][1] + a[u];
        else if(dp2[u][2] > dp1[to][1] + a[u])dp2[u][2] = dp1[to][1] + a[u];
    }
    if(!d[u])dp1[u][1]=dp1[u][2]=dp2[u][1]=dp2[u][2]=a[u];
}
ll up1[MAXN],up2[MAXN];

void dfs2(ll fa,ll u)
{
    ll len=v[u].size();
    for(ll i=0;i<len;i++){
        ll vv = v[u][i];
        if(vv == fa)continue;
        if (d[u]==1) up1[vv]=up2[u]+a[vv],up2[vv]=up1[u]+a[vv];
        else{
            ll Max = dp1[u][1];
            if(dp1[u][1] == dp2[vv][1] + a[u]){
                Max = dp1[u][2];
            }
            if(u!=1)Max=max(Max,up2[u]);
            up1[vv] = Max + a[vv] ;

            ll Min = dp2[u][1];
            if(dp2[u][1] == dp1[vv][1] +a[u]){
                Min = dp2[u][2];
            }
            if(u!=1)Min=min(Min,up1[u]);
            up2[vv] = Min + a[vv] ;
        }
        dfs2(u,vv);
    }
}

int main()
{
    ll t;
    scanf("%lld",&t);
    while(t--)
    {
        scanf("%lld",&n);
        for(ll i=1;i<=n;i++)v[i].clear();
        for(ll i=1;i<=n;i++){
            scanf("%lld",&a[i]);
        }
        for(ll i=1;i<=n;i++){
            ll b;
            scanf("%lld",&b);
            a[i]-=b;
        }
        for(ll i=1;i<=n;i++){
            d[i]=0;
            dp1[i][1]=dp1[i][2]=-inf;
            dp2[i][1]=dp2[i][2]=inf;
        }
        for(ll i=1;i<n;i++){
            ll uu,vv;
            scanf("%lld%lld",&uu,&vv);
            v[uu].push_back(vv);
            v[vv].push_back(uu);
        }
        dfs(0,1);
        up1[1]=up2[1]=a[1];
        dfs2(0,1);
        ll ans = dp2[1][1];
        for(ll i=2;i<=n;i++){
            if(v[i].size()!=1)ans=max(ans,min(up1[i],dp2[i][1]));
            else ans=max(ans,up1[i]);
        }
        printf("%lld\n",ans);
    }
}