李宏毅机器学习笔记（三）

1.梯度下降（Gradient Descent）

在求解使得损失函数（L:loss function）最小的过程中，使用到了梯度下降，即：

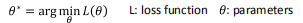
若参数有两个维度，则两个维度的不同的参数按以下得到：

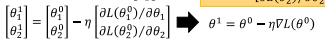
其中：

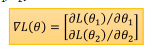
下一次的梯度移动方向为前一次梯度方向的反方向：

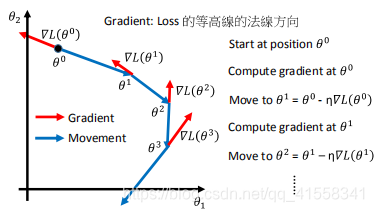
对于梯度下降的三个建议

1. 调整 learning rate
   不同的学习率，LOSS随着参数更新的变化情况不一样：
   

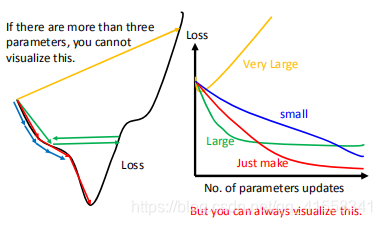
• 适应性地调整learning rate
• 基本思想：每一次迭代，根据一些因素，减少learning rate
  不能对全局迭代过程使用一个learning rate。

-Adagrad

Adagrad与普通的梯度下降之间的区别：

其中：

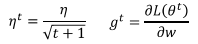
并有如下的迭代关系：

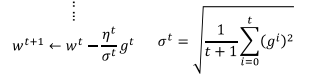
带入表达式，可得：

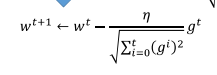
分子和分母貌似在step的更新上是朝着相反方向的，看似矛盾：

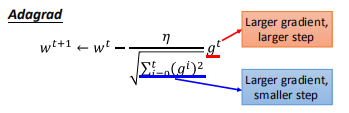
这里一个直观的解释：
当梯度变化很大时，最新的一次迭代的分母会变化很大，使得learning rate 变小。

以二次函数为例，发现Best step：

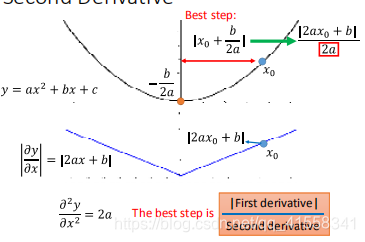
和一次微分成正比，与二次微分成反比。
在Adagrad中，分母用梯度的平方和根值来近似表现二次微分的值：

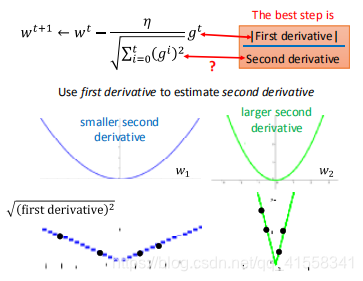
较大的一次微分的平方和根值，其二次微分值也越大。

2.随机梯度下降（Stochastic Gradient Descent）

通常L是对所有example求误差只和，而stochastic是对某一个example求L,更新参数更快，

3.特征缩放（feature scaling）
使不同维度的特征放缩到同个单位区间内：

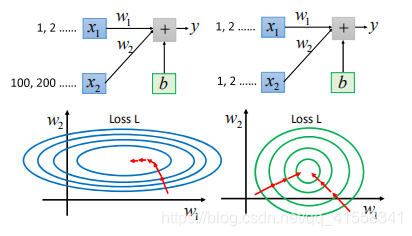
两个维度不一致时，需要调整learning rate，顺着梯度方向，即等高线方向，距离梯度最小的圆心仍然有差距，而在右图，同一个learning rate即可，也是向圆心（如果两个维度相同，是一个正圆）。
具体做法：
对不同的数据的同一个维度(同一个特征)进行求均值以及标准差的方法，对数据进行归一化处理，最终，所有的维度的均值为0，方差为1.

从泰勒级数推导梯度下降

若参数有两个维度的值，考虑如何找到其附近的最小值。
由泰勒级数：

泰勒级数成立的条件是x在x0附近无限可微。
多变量的泰勒级数如下：
类比到本例就是红圈足够小：

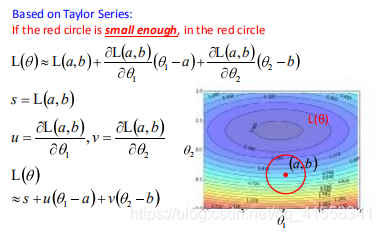
为了在图中找到满足条件的点，使得L最小，又满足，参数的两个维度参数在红圈内：

根据向量的内积（inner product）取最小的原则，u，v与△是反向相反的关系，所以有如下关系，其中learning rate与红圈的大小有关：

将u，v回代，就得到了梯度下降的来源：

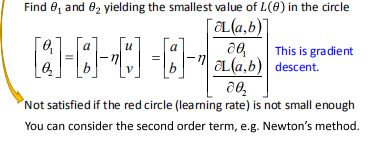
• 对于不满足learning rate足够小的条件，可以考虑二阶项，即牛顿法。