【ZOJ 4097 & The 19th Zhejiang University Programming Contest H】Rescue the Princess【边双连通缩点+LCA】

题意：

给出一个无向图，$n$个点，$m$条边，可能有重边与自环，也可能不连通。$q$ 组询问，每组询问给出$3$个点，$u$、$v$、$w$，问是否存在两条路径不存在公共边，并且一条路径是$v\to u$，另一条路径是$w\to u$，存在输出$Yes$，否则输出$No$. $(1\le n\le 10^5,0\le m\le 2\ast 10^5,1\le q\le 10^5)$

---

思路：

既然是无向图上求两条互不相交的路径，比较直接的想法就是先求出边双连通分量进行缩点，然后在树上进行考虑。

求出边双连通分量之后，假如 $u$、$v$、$w$ 三点在同一个双连通分量中，则答案必定为$Yes$。若 $v$、$w$ 在同一个双连通分量中，而$u$在另一个双连通分量中，则答案必定为$No$。若$v$或$w$和$u$在同一个双连通分量中，另一个点不在其中，则答案也为$Yes$。考虑完了一个和两个双连通分量的情况之后，我们来考虑三个的情况。

假如 $u$、$v$、$w$ 分属于三个不同的双连通分量中，则需要进行分类。$Yes$ 的情况只有两种，第一种情况是$v$和$w$都在$u$子树中，即$lca(v,w)=u$即可，如图$(1)$。第二种情况是$v$、$w$中有一个在$u$的子树中，另一个则不在。对于这种情况，我们先求出$lca(v,w)=y$，再求出$x_1=lca(u,w),x_2=lca(u,v)$，则$x_1$与$x_2$中一定有一个为$y$，另一个为$u$，才能输出$Yes$，否则输出$No$. 到此，这题分类讨论就结束了。

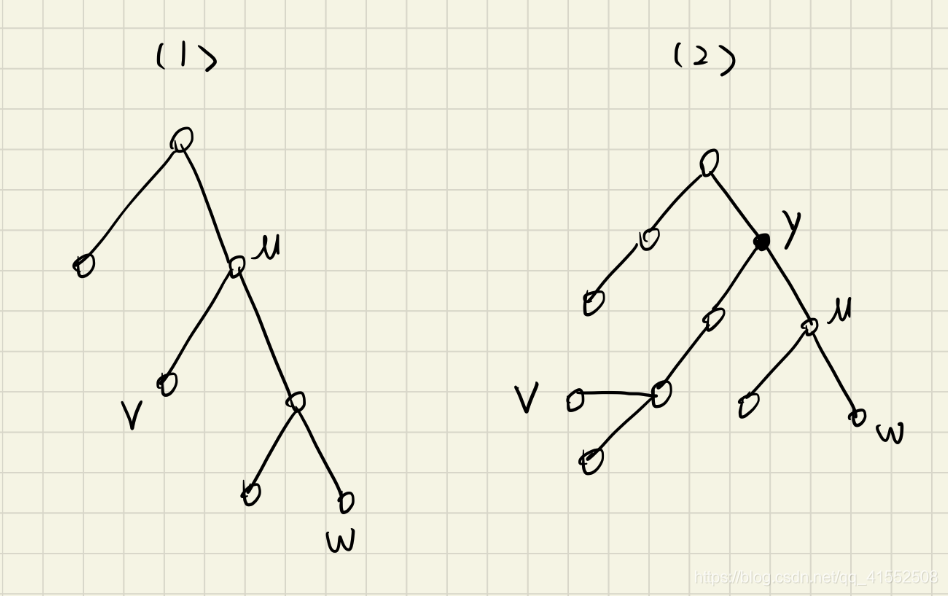
但是这一题还需要注意一些细节，因为图可能不连通，因此需要预先判断$u$、$v$、$w$三个点是否连通，如果不连通，直接输出$No$. 还有一个细节，因为图可能是个森林，因此需要对每一个树进行 $lca$ 处理。

---

反思：

比赛的时候想法的确是正确的，也考虑到了图不连通这一特殊情况。但是忘记了图不连通时，需要对森林中每一颗树预处理一遍 $lca$，导致最终也没有通过此题，实力还是非常有待提升，继续加油！！

---

代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
#define __ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define rep(i,a,b) for(int i = a; i <= b; i++)
#define LOG1(x1,x2) cout << x1 << ": " << x2 << endl;
#define LOG2(x1,x2,y1,y2) cout << x1 << ": " << x2 << " , " << y1 << ": " << y2 << endl;
#define LOG3(x1,x2,y1,y2,z1,z2) cout << x1 << ": " << x2 << " , " << y1 << ": " << y2 << " , " << z1 << ": " << z2 << endl;
typedef long long ll;
typedef double db;
const int N = 2*1e5+100;
const int M = 5*1e5+100;
const db EPS = 1e-9;
using namespace std;

struct Edge{	
	int to,next;
}e[M],ec[M];
int n,m,q,head[N],dfn[N],low[N],headc[N],dis[N],d[N],f[N][20],t;
bool bridge[M];
int tot,num,dcc,tc,DD[N];
int c[N];

void init(){
	tot = tc = 1;
	num = dcc = 0;
	rep(i,0,n) head[i] = headc[i] = 0;
	rep(i,0,2*m) bridge[i] = 0;
	rep(i,0,n) c[i] = dfn[i] = low[i] = 0;
	rep(i,0,n) dis[i] = d[i] = DD[i] = 0;
}

void add(int x,int y){
	e[++tot].to = y; e[tot].next = head[x]; head[x] = tot; 
}

void addc(int x,int y)
{
	ec[++tc].to = y; ec[tc].next = headc[x]; headc[x] = tc;
}

void tarjan(int x,int in_edge)
{
	dfn[x] = low[x] = ++num;
	for(int i = head[x]; i ; i = e[i].next)
	{
		int y = e[i].to;
		if(!dfn[y]){
			tarjan(y,i);  //传入边(x,y)的序号
			low[x] = min(low[x],low[y]);
			if(low[y] > low[x])  //该边连接(x,y)，y点无法连接x点上面的点，因此该边是割边
				bridge[i] = bridge[i^1] = true;
		}
		else if(i != (in_edge^1)) //y点所连接的边 不能是(x,y)边的反向边
			low[x] = min(low[x],dfn[y]);
	}
}

void dfsD(int x,int hp){
	DD[x] = hp;
	for(int i = head[x]; i; i = e[i].next){
		int y = e[i].to;
		if(DD[y] == 0) dfsD(y,hp);
	}
}

void dfs(int x)	//用于将图划分为多个边双连通分量
{
	c[x] = dcc;
	for(int i = head[x]; i ; i = e[i].next)
	{
		int y = e[i].to;
		if(c[y] || bridge[i]) continue;  //如果点y已经属于别的强连通分量，或者边i是割边，则continue
		dfs(y);
	}
}

void bfs(int s)
{
	queue<int> q;
	while(q.size()) q.pop();
	q.push(s); d[s] = 1; dis[s] = 0;	//把1当做树根
	while(q.size())
	{
		int x = q.front(); q.pop();
		for(int i = headc[x]; i ;i = ec[i].next){
			int y = ec[i].to;
			if(d[y]) continue;
			d[y] = d[x]+1;
			dis[y] = dis[x]+1;	//dist[y]:从1到y的距离
			f[y][0] = x;  //y走2^0步到达x
			for(int j = 1; j <= t;j++)
				f[y][j] = f[f[y][j-1]][j-1];
			q.push(y);
		}
	}
}

int lca(int x,int y)
{
	if(d[x] > d[y]) swap(x,y);
	for(int i = t; i >= 0; i--)
		if(d[f[y][i]] >= d[x]) y = f[y][i];  //往上追溯，直至y和x位于同一深度
	if(x == y) return x;  //如果已经找到了，就返回x
	for(int i = t; i >= 0; i--)
		if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];  //x和y同时往上走，一直到x和y恰好为lca的子节点
	return f[x][0];  //x和y共同的根节点就是lca 
}


int main()
{
	int _; scanf("%d",&_);
	while(_--){
		scanf("%d%d%d",&n,&m,&q);
		init();
		rep(i,1,m){
			int xx,yy; scanf("%d%d",&xx,&yy);
			add(xx,yy); add(yy,xx);
		}
		int ctt = 0;
		rep(i,1,n)
			if(!DD[i]) dfsD(i,++ctt);
		rep(i,1,n)
			if(!dfn[i]) tarjan(i,0); //将边序号传进去
		rep(i,1,n)
			if(!c[i]){ //如果i点未被标记过
				++dcc;
				dfs(i);
			}
		rep(i,2,tot){
			int x = e[i^1].to, y = e[i].to; //记录该边连接的两个端点
			if(c[x] == c[y]) continue; //如果连接的两个点属于同一连通分量，则continue
			addc(c[x],c[y]);  //用连通的分量的编号来代表整个连通分量，以此来进行缩点
			addc(c[y],c[x]);
		}
		t = (int)(log(dcc+1)/log(2))+1;
		rep(i,1,dcc)
			if(d[i] == 0) bfs(i);
		rep(i,1,q){
			int u,v,w; scanf("%d%d%d",&u,&v,&w);
			if(DD[u] == DD[v] && DD[u] == DD[w]){
				if(c[u] == c[v] && c[u] == c[w]) printf("Yes\n");
				else if(c[v] == c[w] && c[v] != c[u]) printf("No\n");
				else if(c[u] != c[v] && c[u] != c[w] && c[v] != c[w]){
					int y = lca(c[v],c[w]);
					if(y == c[u]) printf("Yes\n");
					else{
						int x1 = lca(c[v],c[u]);
						int x2 = lca(c[w],c[u]);
						if(x1 == y && x2 == c[u]) printf("Yes\n");
						else if(x2 == y && x1 == c[u]) printf("Yes\n");
						else printf("No\n");
					}
				}
				else if(c[v] == c[u] && c[w] != c[v]) printf("Yes\n");
				else if(c[w] == c[u] && c[w] != c[v]) printf("Yes\n");
				else printf("No\n");
			}
			else printf("No\n");
		}
	}
	return 0;
}

由于ZOJ不能交题了，再次给出数据生成代码，以供对拍。（ZOJ现在可以交题了，题目可以在Problem里面找到）

#include <iostream>
#include <cstdlib>
#include <ctime>
#define rep(i,a,b) for(int i = a; i <= b; i++)
using namespace std;

char tmp[10] = {'I','S','F','A'};
int vis[1000];

int main()
{
    freopen("/Users/gene_liu/Desktop/pai/text.txt","w",stdout);
    srand(time(0));
    int n = 1e5, m = 2*1e5, q = 1e5;
	printf("1\n%d %d %d\n",n,m,q);
	rep(i,1,m){
		int x = rand()%n+1, y = rand()%n+1;
		printf("%d %d\n",x,y);
	}
	rep(i,1,q){
		int u = rand()%n+1, v = rand()%n+1, w = rand()%n+1;
		printf("%d %d %d\n",u,v,w);
	}
	return 0;
}