LeetCode_Array_221. Maximal Square 最大正方形【动态规划，模拟】【Java】【中等】

本文链接：https://blog.youkuaiyun.com/qq_41528502/article/details/124254506

一，题目描述

英文描述

Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

中文描述

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例与说明

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 '0' 或 '1'

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximal-square
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

二，解题思路

参考@lzhlyle【理解三者取最小+1】

动态规划。大佬给出的题解很清晰了，核心就是一张图

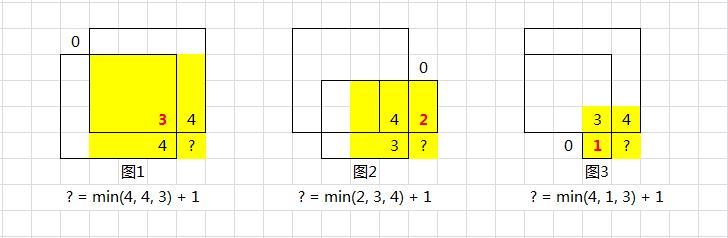
dp数组中存放的是以当前位置为右下角的最大正方形的边长。

为什么选择右下角而不是左上角？这个和dp填表（习惯把dp过程看作填表）的顺序有关，一般比较习惯的思路是自左向右、自上而下。如果选择当前位置为正方形左上角的话，就需要反过来进行填表遍历。

三，AC代码

Java（二维dp）

class Solution {
    public int maximalSquare(char[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        int maxSide = 0;
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (matrix[i - 1][j - 1] == '1') {
                    dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
                    maxSide = Math.max(maxSide, dp[i][j]);
                }
            }
        }
        return maxSide * maxSide;
    }

}

二维dp转一维也是比较常见的优化方法，只需要注意提前保留旧值，避免新值覆盖旧值即可。

四，解题过程

第一搏

硬模拟，细节注意点不太难

class Solution {
    public int maximalSquare(char[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        Queue<int[]> queue = new LinkedList<>();
        // 记录matrix中所有字符1 的位置，作为初始位置
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') {
                    int[] pos = new int[]{i, j};
                    queue.offer(pos);
                }
            }
        }

        int ans = 1;// 记录当前得到最大正方形边的大小
        while (!queue.isEmpty()) {
            int num = queue.size();
            // 将边长为ans的正方形依次弹出，看看有没有位置能扩展一个单位
            while (num-- != 0) {
                int[] pos = queue.peek();
                queue.poll();
                if (canExtend(matrix, pos, ans)) {
                    queue.offer(pos);
                }
            }
            ans++;// 将正方形的边长扩展一个单位
        }
        ans--;// 跳出循环时表明无法继续扩展，所以这里要减一
        return ans * ans;
    }

    // 判断matrix中，以pos记录的位置为左上角位置，能否将正方形扩展一个单位
    public boolean canExtend(char[][] matrix, int[] pos, int edgeSize) {
        int m = matrix.length, n = matrix[0].length;
        
        if (pos[0] + edgeSize >= m || pos[1] + edgeSize >= n) return false;// 避免越界

        for (int i = pos[0]; i <= pos[0] + edgeSize; i++) {
            if (matrix[i][pos[1] + edgeSize] == '0') return false;
        }
        for (int j = pos[1]; j < pos[1] + edgeSize; j++) {
            if (matrix[pos[0] + edgeSize][j] == '0') return false;
        }
        return true;
    }
}