Python手册(Machine Learning)--statsmodels(GettingStarted)

本站已停止更新，查看最新内容请移至本人博客 https://wilenwu.gitee.io

statsmodels
与scikit-learn比较，statsmodels包含经典统计学和经济计量学的算法。包括如下子模块：

• 回归模型：线性回归，广义线性模型，健壮线性模型，线性混合效应模型等等。
• 方差分析（ANOVA）。
• 时间序列分析：AR，ARMA，ARIMA，VAR和其它模型。
• 非参数方法： 核密度估计，核回归。
• 统计模型结果可视化。

statsmodels更关注统计推断，提供不确定估计和参数p-value。相反的，scikit-learn注重预测。

---

Python手册(Machine Learning)–statsmodels(GettingStarted)
Python手册(Machine Learning)–statsmodels(Regression)
Python手册(Machine Learning)–statsmodels(ANOVA)
Python手册(Machine Learning)–statsmodels(Tables+Imputation)
Python手册(Machine Learning)–statsmodels(MultivariateStatistics)
Python手册(Machine Learning)–statsmodels(TimeSeries)
Python手册(Machine Learning)–statsmodels(Survival)
Python手册(Machine Learning)–statsmodels(Graphics)

---

模型拟合和描述

>>> import statsmodels.api as sm
>>> import statsmodels.formula.api as smf
>>> import pandas
>>> df = sm.datasets.get_rdataset("Guerry", "HistData").data
>>> df = df.dropna()
# step 1 Describe model,return model class
>>> mod = smf.ols(formula='Lottery ~ Literacy + Wealth + Region', data=df)
# step 2 Fit model,return result class
>>> res = mod.fit()
# step 3 Summarize model
>>> print(res.summary())
 OLS Regression Results                            
==============================================================================
Dep. Variable:                Lottery   R-squared:                       0.338
Model:                            OLS   Adj. R-squared:                  0.287
Method:                 Least Squares   F-statistic:                     6.636
Date:                Sun, 23 Dec 2018   Prob (F-statistic):           1.07e-05
Time:                        18:41:19   Log-Likelihood:                -375.30
No. Observations:                  85   AIC:                             764.6
Df Residuals:                      78   BIC:                             781.7
Df Model:                           6                                         
Covariance Type:            nonrobust                                         
===============================================================================
                  coef    std err          t      P>|t|      [0.025      0.975]
-------------------------------------------------------------------------------
Intercept      38.6517      9.456      4.087      0.000      19.826      57.478
Region[T.E]   -15.4278      9.727     -1.586      0.117     -34.793       3.938
Region[T.N]   -10.0170      9.260     -1.082      0.283     -28.453       8.419
Region[T.S]    -4.5483      7.279     -0.625      0.534     -19.039       9.943
Region[T.W]   -10.0913      7.196     -1.402      0.165     -24.418       4.235
Literacy       -0.1858      0.210     -0.886      0.378      -0.603       0.232
Wealth          0.4515      0.103      4.390      0.000       0.247       0.656
==============================================================================
Omnibus:                        3.049   Durbin-Watson:                   1.785
Prob(Omnibus):                  0.218   Jarque-Bera (JB):                2.694
Skew:                          -0.340   Prob(JB):                        0.260
Kurtosis:                       2.454   Cond. No.                         371.
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
>>> res.params  # 获取模型参数
Intercept      38.651655
Region[T.E]   -15.427785
Region[T.N]   -10.016961
Region[T.S]    -4.548257
Region[T.W]   -10.091276
Literacy       -0.185819
Wealth          0.451475
dtype: float64
>>> dir(res)    # 查看完整的属性列表

输入输出模型

from statsmodels.iolib import smpickle
smpickle.save_pickle(obj, fname)	#Save the object to file via pickling.
smpickle.load_pickle(fname)	#Load a previously saved object from file

模型测试和绘图

>>> #Rainbow测试线性度（零假设是关系被正确建模为线性)
>>> sm.stats.linear_rainbow(res)
(0.847233997615691, 0.6997965543621644)
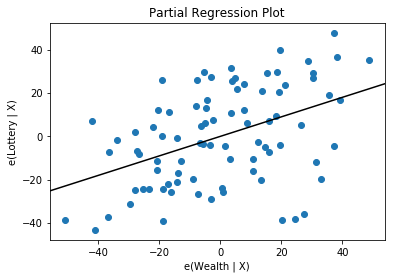
>>> sm.graphics.plot_partregress('Lottery', 'Wealth', ['Region', 'Literacy'],
      data=df, obs_labels=False) #绘制回归图

使用R型公式来拟合模型

import statsmodels.formula.api as smf

formula	说明	示例
~	分隔符，左边为响应变量，右边为解释变量
+	添加变量	y~x+y
-	移除变量	y~xzw–x:z:w可展开为 y ~ (x + z + w)**2
-	移除变量	y~x-1(移除截距)
:	预测变量交互项	y~x+y+x:y
*	包含所有交互项的简洁方式	代码y~ x * z可展开为y ~ x + z + x:z
**	交互项的最高次数	代码 y ~ (x + z + w)**2 可展开为 y ~ x + z + w + x:z + x:w + z:w
C()	处理分类变量
function	数学函数	log(y) ~ x + z + w

支持R型公式的模型

In [15] res = smf.ols(formula='Lottery ~ Literacy + Wealth + C(Region) -1 ', data=df).fit()

不支持R型公式的模型，使用patsy 模块

#Using formulas with models that do not (yet) support them
In [22]: import patsy
In [23]: f = 'Lottery ~ Literacy * Wealth'
In [24]: y, X = patsy.dmatrices(f, df, return_type='matrix')
 #y被转化为patsy.DesignMatrix,x被转化为转化为numpy.ndarray
In [26]: print(X[:5])
[[   1.   37.   73. 2701.]
 [   1.   51.   22. 1122.]
 [   1.   13.   61.  793.]
 [   1.   46.   76. 3496.]
 [   1.   69.   83. 5727.]]
In [27]: f = 'Lottery ~ Literacy * Wealth'

In [28]: y, X = patsy.dmatrices(f, df, return_type='dataframe') #转化为pandas.dataframe
In [30]: print(X[:5])
   Intercept  Literacy  Wealth  Literacy:Wealth
0        1.0      37.0    73.0           2701.0
1        1.0      51.0    22.0           1122.0
2        1.0      13.0    61.0            793.0
3        1.0      46.0    76.0           3496.0
4        1.0      69.0    83.0           5727.0
In [31]: res=smf.OLS(y, X).fit()

statsmodels参数

Statsmodels使用endog和exog为模型数据参数名称，作为估计器的观测变量。

endog	exog
y	x
y variable	x variable
left hand side (LHS)	right hand side (RHS)
dependent variable（因变量）	independent variable（自变量）
regressand	regressors
outcome	design
response variable（响应变量）	explanatory variable（解释变量）

模型和拟合结果的超类

Model和Result是statsmodels所有模型和结果的父类

model class

Model(endog, exog=None, **kwargs) #建立模型

Methods	desc
fit()	Fit a model to data.
from_formula(formula, data, subset=None, drop_cols=None, *args, **kwargs)	Create a Model from a formula and dataframe.
predict(params, exog=None, *args, **kwargs)	After a model has been fit predict returns the fitted values.

Attributes	desc
endog_names	Names of endogenous variables
exog_names	Names of exogenous variables

result class

Results(model, params, **kwd) #一般通过模型fit方法拟合生成

Methods	desc
initialize(model, params, **kwd)
predict([exog, transform])	Call self.model.predict with self.params as the first argument.
summary()