机器学习（七）——逻辑回归

1. 逻辑回归

逻辑回归就是对多元线性回归的缩放

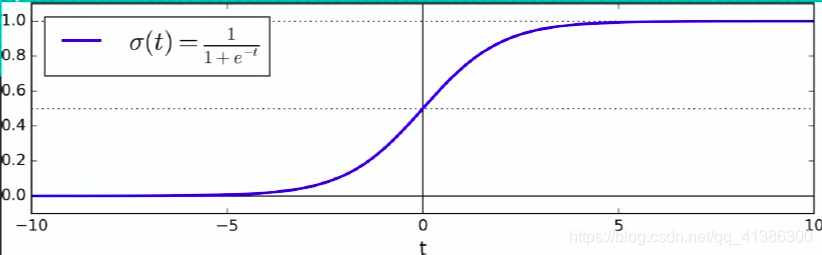
公式如上图，其中t就是多元线性回归的公式：w的转置 * X，逻辑回归的y的取值范围为（0，1），而多元线性回归的y的取值范围是负无穷到正无穷

逻辑回归适合做二分类，用0.5做间隔，大于0.5是一类，小于0.5是另一类

知识点：

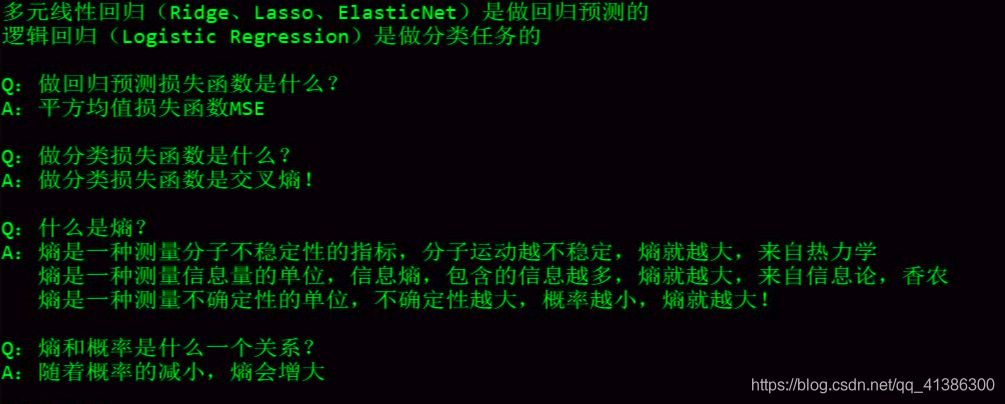
代码实现鸢尾花案例——二分类：

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
import matplotlib.pyplot as plt
from time import time

iris = datasets.load_iris()  # 鸢尾花数据集，可以点进源码看一下，介绍的很详细
# print(list(iris.keys()))  # ['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename']
# print(iris['DESCR'])  # 从结果中可以看出，花瓣petal的长度和宽度和结果的相关性更高，所以花萼的数据就可以不要了
# print(iris['feature_names'])  # 特征名 ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

X = iris['data'][:, 3:]  # 取花瓣宽度这一列数据
# print(X)
#
# print(iris['target'])
y = iris['target']
# print(y)

# multi_class='ovr'是二分类，还可以选择多分类；solver="sag"表示用梯度下降的方法
log_reg = LogisticRegression(multi_class='ovr', solver="sag")
log_reg.fit(X, y)


X_new = np.linspace(0, 3, 1000).reshape(-1, 1)  # 在（0，3）区间内平均分成1000段，取这1000个点作为x
# print(X_new)

y_proba = log_reg.predict_proba(X_new)  # 预测分类概率
y_hat = log_reg.predict(X_new)  # 预测分类号
# print(y_proba)
# print(y_hat)

plt.plot(X_new, y_proba[:, 2], 'g-', label='Iris-Virginica')
plt.plot(X_new, y_proba[:, 1], 'r-', label='Iris-Versicolour')
plt.plot(X_new, y_proba[:, 0], 'b--', label='Iris-Setosa')
plt.show()

print(log_reg.predict([[1.7], [1.5]]))

输出结果：[ 2 , 1 ]

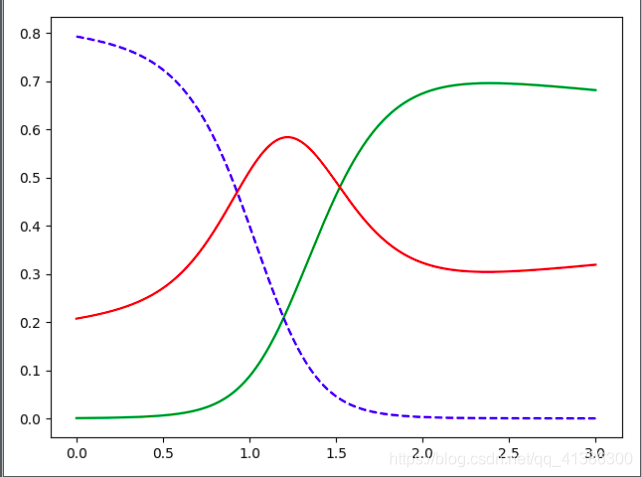
用逻辑回归做多分类：就是把一个多分类转化为多个二分类

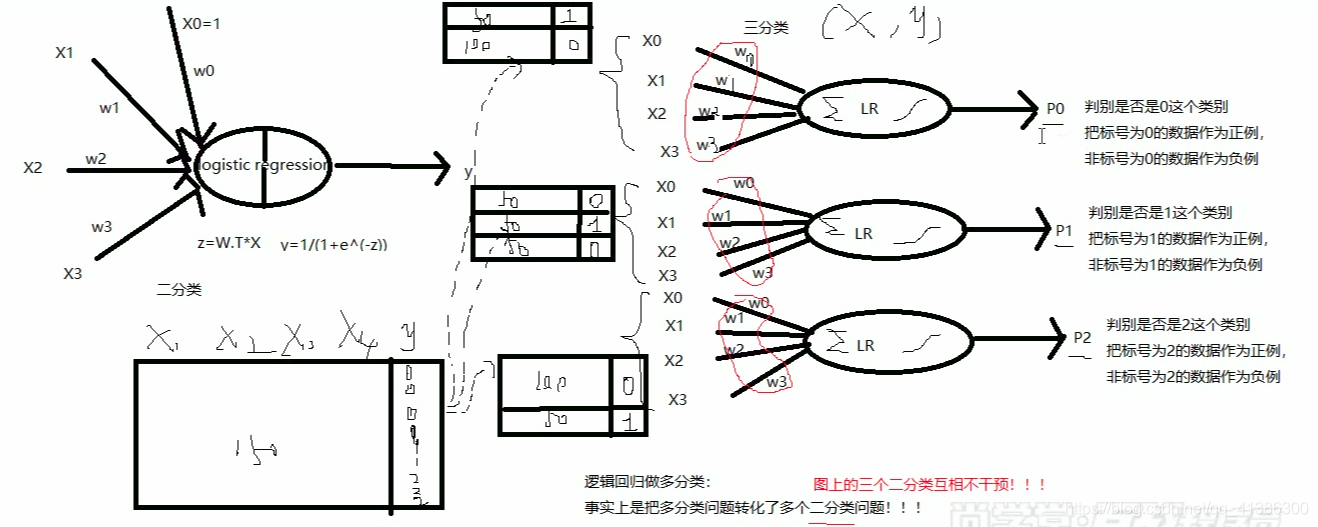
假设要做一个三分类：就是做三次二分类，取三个结果中的概率最大者为最终结果
总结：