机器学习（六）——多项式回归及通过案例学习做预测的流程

1. 多项式回归Polynomial regression

有的时候我们的数据可能是非线性的变化，这个时候我们的线性模型就拟合不了了，怎么办呢？两种方法：
（1）用非线性的算法
（2）把数据变成线性的
而多项式回归是用来做特征转换的，就是用第二种方法

从上图中可以知道，多项式回归就是在升维（把两个维度的x变成里6个维度）
例如：
当原来只有两个维度x0，x1 升维度后（二阶）就变成了三个： x0， x1， x1^2 如果是三阶： x0， x1， x1 ^2， x1 ^3
原来只有三个维度：x0,x1,x2 升维后（二阶）六个维度：x0， x1， x2 ，x1^2， x2 ^2， x1x2 三阶：多个 x1 ^3 x2 ^3
原来又四个维度：x0， x1， x2， x3 升维后（二阶）十个： x0， x1，x2，x3， x1^2， x2 ^2， x3 ^2， x1x2， x2x3， x1x3 三阶： 多个x1 ^3， x2 ^3， x3 ^3
代码实现：
我们线看一下非线性的数据

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

m = 100
X = 6 * np.random.rand(m, 1) - 3 #本来范围是（0，1）*6之后变成了（0，6），-3后变成了（-3，3）
# 有了平方，数据就不是线性的了（不是一条直线），
y = 0.5 * X ** 2 + X + 2 + np.random.randn(m, 1)# 相当于w0=2,w1=1,w3=0.5

plt.plot(X, y, 'b.')
plt.show()

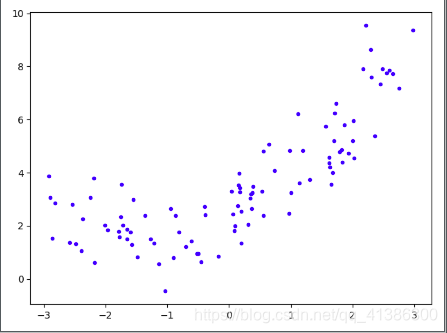
从图中我们可以看出来它不是一条直线，是一条抛物线，非线性的

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

m = 100
X =</