算法金 | 一个强大的算法模型，多项式回归！！

大侠幸会，在下全网同名「算法金」 0 基础转 AI 上岸，多个算法赛 Top 「日更万日，让更多人享受智能乐趣」

吴恩达：机器学习的六个核心算法！–> 线性回归

在许多实际场景中，简单的线性回归无法捕捉复杂的模式，这时候就该祭出我们多项式回归大法了，一种在数据分析和预测中常用的机器学习方法。

本文的目的在于为大侠们提供多项式回归的基础理解，并通过代码示范和数据可视化，展示如何在实践中应用这一技术。同时，本文将避免过多复杂的数学推导，侧重于实用性和可操作性。

1. 多项式回归简介

1.1 什么是多项式回归

多项式回归是对线性回归的一种扩展，它通过添加多项式项来拟合数据中的非线性关系。其基本思想是将原始特征扩展为多项式特征，然后应用线性回归模型。多项式回归的方程形式如下：

1.2 多项式回归 vs 线性回归

线性回归: 线性回归假设目标变量和特征变量之间存在线性关系，即：

这种方法在特征与目标变量呈线性关系时效果很好，但在处理复杂的非线性关系时表现较差。

多项式回归: 多项式回归通过引入高次项来拟合数据的非线性关系，如上节所述。通过增加多项式的阶数，可以捕捉到更多复杂的模式，但同时也增加了模型的复杂性和过拟合的风险。

1.3 多项式回归的适用场景

多项式回归适用于以下场景：

• 数据中的非线性关系显著，如某些时间序列预测、经济数据分析等。
• 需要通过模型捕捉复杂的模式和趋势。
• 有足够的数据支持模型训练，避免过拟合风险。

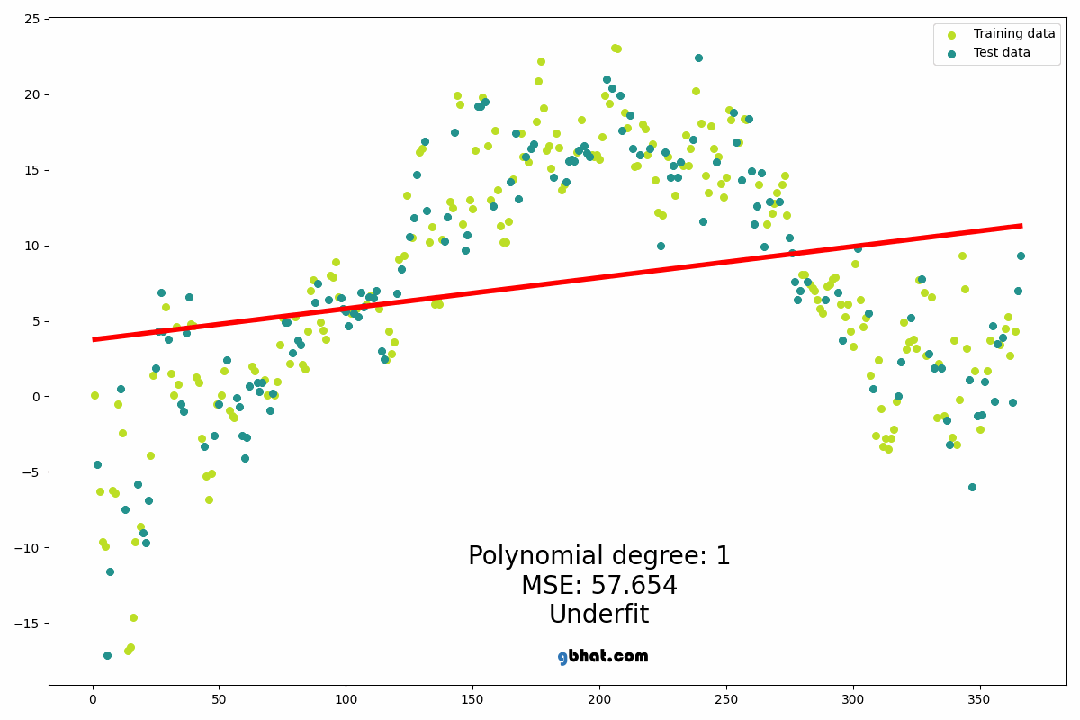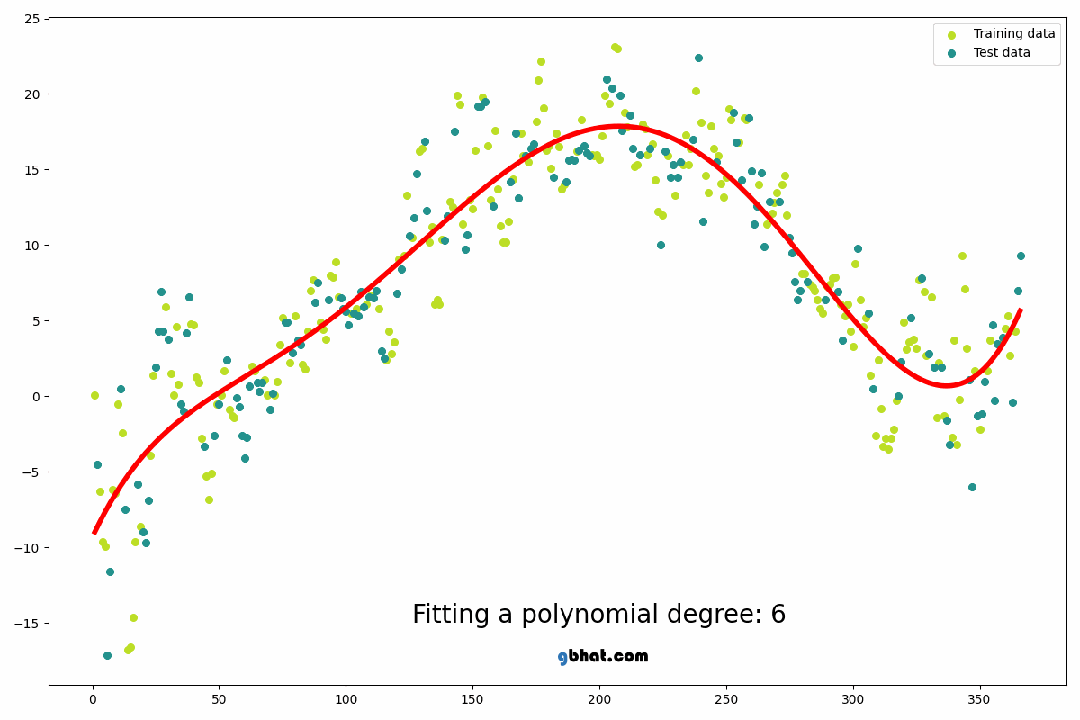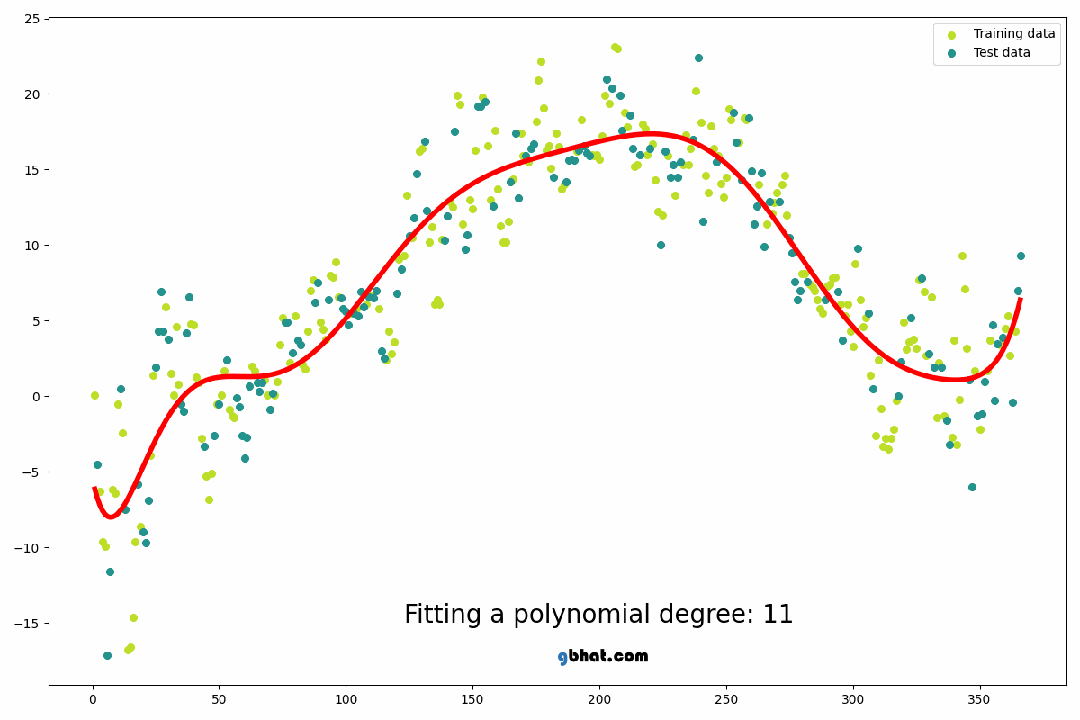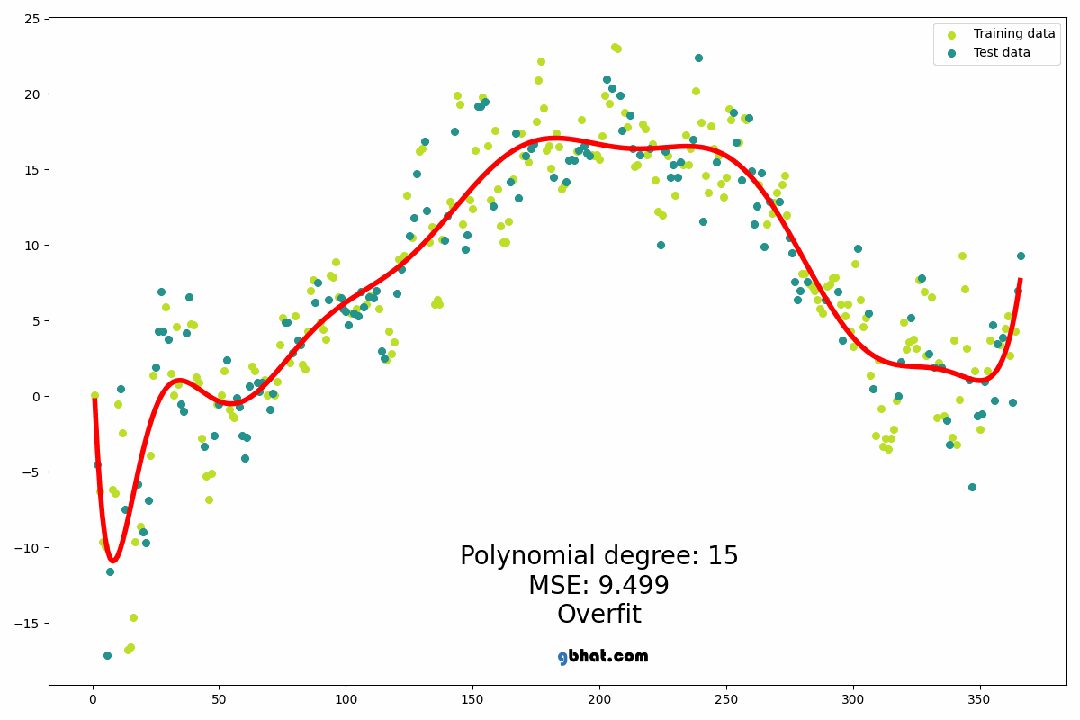
2. 多项式回归的数学公式

2.1 多项式回归方程

多项式回归的基本方程是通过在线性回归模型中加入多项式特征来构建的。其一般形式为：