MATLAB时间序列2（ARIMA,季节性序列及其预报）------2019/8/14

时间序列(时间序列模型只适合短时期预测，不适合长时期)

• 平稳时间序列
  
  
  1）平稳性检验及自协方差函数、自相关函数的估计
     1．平稳性 Daniel 检验
  
  

x0=[1.37 2.96 1.91 3.10 2.08 2.54 4.07 3.62 2.91 1.94 3.96 4.19 2.71 3.42 3.02 3.54 2.66 4.11 4.25 3.76];
x0=x0';
x0=x0(:)';
n=length(x0);
alpha=0.05
[xsort,ind]=sort(x0);
%按从小到大的次序排列数据
%[B,I] = sort(A,dim),B - 已排序数组;I - 排序索引

rt(ind)=1:n;
%计算秩

t=1:n;

qs=1-6/(n*(n^2-1))*sum((t-rt).^2)
%计算qs的值，

t=qs*sqrt(n-2)/sqrt(1-qs^2)
%计算 t 统计量的值

t_0=tinv(1-alpha/2,n-2)
%计算上 alpha/2的分位点
%若t>t_0,则拒绝H0，认为序列是非平稳的，若qs>0,则序列有上升趋势

2. ARMA 时间序列及其特性
   $$ARMA时间序列=\{\begin{array}{l}AR模型，即自回归序列\\ MA序列，即滑动平均序列\\ ARMA序列，即自回归滑动平均序列\end{array}$$
   理论描述没懂
   

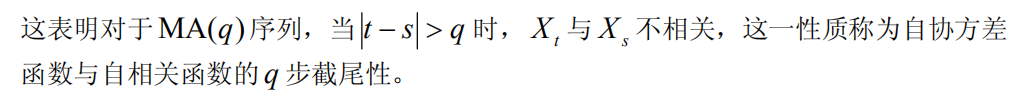
（性质太多，不写了。看书吧《数学建模算法与应用》p507）

• ARIMA 序列与季节性序列
  
  
   设 $X_t$ 是$ARIMA(p,d,$