本博客来源于优快云机器鱼,未同意任何人转载。
更多内容,欢迎点击本专栏目录,查看更多内容。
目录
目录
0.引言
针对滚动轴承故障问题,提出一种基于经验模态分解–希尔伯特(empirical mode decomposition-Hilbert ,简称EMD-Hilbert)包络谱和堆栈自动编码器(Stack denoise auto-encoder,简称SDAE)的滚动轴承故障识别方法。该方法首先对滚动轴承各状态振动信号进行 EMD,然后选取前5个敏感本征模态函数 (intrinsic mode function,IMF),并对其进行 Hilbert 变换求取包络谱。最后将各状态振动信号的IMF包络谱按顺序拼接构建新的高维数据,输入到SDAE中,实现故障识别。同时,由于提取的IMF包络谱特征维数过高,采用PCA对其中可能包含的冗余特征进行剔除。对比实验结果显示,采用包络谱+PCA+SDAE方法得到的故障识别正确率最高。
1.方法原理
1.1 EMD-HHT包络谱
参考文献【基于 EEMD-Hilbert 包络谱和 DBN 的 变负载下滚动轴承状态识别方法】,EMD-HHT包络谱求取步骤为:1)对信号进行EMD分解;2)分别对每个分量做hilbert变换,得到包络线;3)对每个分量的包络线做FFT分析,得到最终特征数据。由于EMD分解出的分量个数并不确定,因此仅取其前5个分量做上述操作。
1.2 PCA
主成分分析的原理就不说了。因为包络谱含有各种频率下的特征,或许某些低频特征是无用的、冗余的,这些特征不会提高分类器性能,反而会降低性能,因此采用PCA进行降维。常用的降维算法还有tSNE、LPP、KPCA等。
1.3 SDAE
这个原理百度就有,可以参考这里,其中本文用的PCA是MATLAB自带的,EMD-HHT与SDAE可以在【这里】下载。
2.流程
如图所示,清晰简明。

3.具体实现
3.1 数据准备
采用西储大学轴承故障诊断数据集,48K/0HP数据,共10类故障(正常作为一类特殊的故障类型),划分后每个样本的采样点为1024,每类故障各200个样本,一共得到2000个样本。博客中用到的数据可在【这里】下载。

3.2 EMD-HHT包络谱求取
3.2.1 画图举例
任意取一个样本做分析,得到EMD分解与归一化后的特征分量如图所示。代码如下所示:
%%
clc;clear;close all
addpath(genpath('pack_emd'))
%下载下来的工具箱解压并改名为pack_emd和此程序放在同一个文件夹下
%% 1、加载原始数据
load 0HP/48k_Drive_End_B007_0_122; data=X122_DE_time';
Fs = 48000; % Sampling frequency
T = 1/Fs; % Sampling period
L = 1024; % Length of signal
t = (0:L-1)*T; % Time vector
X=data(1:L);
figure
plot(t,X)
title('Signal')
xlabel('t (milliseconds)')
ylabel('X(t)')
%% 2、经验模态分解-希尔伯特分解求取包络谱
tz=[];%用于存放每个样本求取的包络谱特征
c=emd(X);%经验模态分解
% 画出 各IMF与残余量
m=size(c,1);
figure
for i=1:m-1
subplot(m,1,i);
set(gcf,'color','w')
plot(c(i,:),'k')
ylabel(['imf',int2str(i)])
end
subplot(m,1,m);
set(gcf,'color','w')
plot(c(m,:),'k')
ylabel('残余量')
xlabel('采样点数')
%IMF太多会影响模型训练速度,因此我们取前5个即可,这样每个样本的特征点为5*N=5*1024/2
%分别求取前5个固有模态函数的包络谱
for i=1:5
y=hilbert(c(i,:));%希尔伯特变换
ydata=abs(y);%包络信号
y_m=ydata-mean(ydata);%去除直流分量
nfft= 2^nextpow2(length(ydata));%计算出FFT步长
f_p=abs(fft(y_m,nfft));
f_p=f_p/max(f_p);%归一化
f_baoluo=f_p(1:nfft/2);
tz=[tz f_baoluo];
end
%% 画第一个IMF对应的包络谱
figure
f_h=(0:nfft/2-1)/nfft*Fs;%hilbert变换后对应的频率的序列
bar(f_h,tz(1:length(f_h)),'k');
grid on
xlabel('频率 f/Hz');
ylabel('归一化包络谱幅值');
%% 画出第一个样本对应的特征样数据
figure
bar(tz,'k');
grid on
xlabel('特征样本点数/个');
ylabel('归一化包络谱幅值');


3.2.2 样本批量处理
对10类数据分别提取200个样本,并依次提取EMD-HHT包络谱,最后将数据划分为训练集与测试集,完整代码如下:
%% 数据预处理(训练集 测试集划分)
clc;clear;close all
%% 加载原始数据
load 0HP/48k_Drive_End_B007_0_122; a1=X122_DE_time'; %1
load 0HP/48k_Drive_End_B014_0_189; a2=X189_DE_time'; %2
load 0HP/48k_Drive_End_B021_0_226; a3=X226_DE_time'; %3
load 0HP/48k_Drive_End_IR007_0_109; a4=X109_DE_time'; %4
load 0HP/48k_Drive_End_IR014_0_174 ; a5=X173_DE_time';%5
load 0HP/48k_Drive_End_IR021_0_213 ; a6=X213_DE_time';%6
load 0HP/48k_Drive_End_OR007@6_0_135 ;a7=X135_DE_time';%7
load 0HP/48k_Drive_End_OR014@6_0_201 ;a8=X201_DE_time';%8
load 0HP/48k_Drive_End_OR021@6_0_238 ;a9=X238_DE_time';%9
load 0HP/normal_0_97 ;a10=X097_DE_time';%10
%%
N1=200;%每类样本的数量
L=1024;
data=[];label=[];
for i=1:10
if i==1;ori_data=a1;end
if i==2;ori_data=a2;end
if i==3;ori_data=a3;end
if i==4;ori_data=a4;end
if i==5;ori_data=a5;end
if i==6;ori_data=a6;end
if i==7;ori_data=a7;end
if i==8;ori_data=a8;end
if i==9;ori_data=a9;end
if i==10;ori_data=a10;end
for j=1:N1
%start_point=randi(length(ori_data)-L);%随机取一个起点
start_point=(j-1)*N1+1;%顺序一个起点
end_point=start_point+L-1;
data=[data ;ori_data(start_point:end_point)];
label=[label;i];
end
end
%% 特征提取
fea=[];
for i =1:size(data,1)
X=data(i,:);
c=emd(X);%经验模态分解
tz=[];
for j=1:5
y=hilbert(c(j,:));%希尔伯特变换
ydata=abs(y);%包络信号
y_m=ydata-mean(ydata);%去除直流分量
nfft= 2^nextpow2(length(ydata));%计算出FFT步长
f_p=abs(fft(y_m,nfft));
f_p=f_p/max(f_p);%归一化
f_baoluo=f_p(1:nfft/2);
tz=[tz f_baoluo];
end
fea=[fea;tz];
end
%% 标签转onehot
l=eye(10);
labels=l(label,:);
%% 划分数据集
% 7:3
index=randperm(size(data,1));
m=round(0.7*size(data,1));
train_x=fea(index(1:m),:);
train_y=labels(index(1:m),:);
test_x=fea(index(m+1:end),:);
test_y=labels(index(m+1:end),:);
save result/data_process train_x train_y test_x test_y
%% 划分原始数据集
% 7:3
index=randperm(size(data,1));
m=round(0.7*size(data,1));
train_x=data(index(1:m),:);
train_y=labels(index(1:m),:);
test_x=data(index(m+1:end),:);
test_y=labels(index(m+1:end),:);
save result/data_original train_x train_y test_x test_y
3.3 SDAE故障诊断
直接采用提取的包络谱进行SDAE建模,代码如下,测试集分类精度为91.5%。
%% 堆栈降噪自动编码器-SDAE用于轴承分类
clc;clear;close all;format compact
addpath(genpath('utils/'))
%下载下来的工具箱解压并改名为utils和此程序放在同一个文件夹下
rng(0)
%% 1.导入数据
load result/data_process % data_original data_process
method=@mapstd;%对数据进行标准化
[xs,mapping]=method(train_x');
xts=method('apply',test_x',mapping);
train_x=xs';
test_x=xts';
%% 网络训练
train_again=1;%#是否重新训练模型,不为1则调用之前保存的模型
if train_again==1
%% 无监督训练多个降噪自动编码器 假设输入维度为 sizes=[n n1 n2],则训练两个ae 一个是n-n1-n 一个是n1-n2-n1
sizes=[size(train_x,2) 50 30 size(train_y,2)]; % 这里 size(train_x,2)为输入层节点数 size(train_y,2)为分类层节点数
learningRate1=0.01;%各dae的学习率
denoise=0.1;%各dae的噪声强度
numepochs1=10;%各dae的训练次数
batchsize1=64;%%各dae的batchsize
activation_function='sigm';%各ae的激活函数
sae = sdaesetup(sizes,activation_function,learningRate1,denoise);
opts.numepochs = numepochs1;
opts.batchsize = batchsize1;
opts.show=0;% 0就不显示训练过程
disp('Train DAEs ')
sae = saetrain(sae, train_x, opts);
%% 构建一个多层前向网络,然后采用上面无监督预训练好的几个DAE的输入层-隐含层权重来初始化,这就叫堆栈降噪自编码器-SDAE
% 然后结合标签进行SDAE的微调训练
learningRate2=0.1;%sae的学习率
numepochs2=500;%sae的训练次数
batchsize2=64;%sae的batchsize
nn = nnsetup(sizes);%构建一个多层前向网络
nn.activation_function= 'sigm';%和上面保持一致
nn.learningRate= learningRate2;
nn=saeunfoldnn(nn,sae);%利用DAE的参数初始化SDAE
opts.numepochs = numepochs2;
opts.batchsize = batchsize2;
nn.output = 'softmax';
opts.show=0;% 0就不显示训练过程
opts.plot = 0;%0就不显示loss曲线
disp('Train SDAE ')
nn = nntrain(nn, train_x, train_y, opts);
disp('训练完毕')
save result/net4 nn
else
load result/net4
end
%% 预测 并计算指标
labels = nnpredict(nn, test_x);
[~, pred] = max(labels,[],2);
[~, real] = max(test_y,[],2);
%% 计算检测的正确率
MatrixClassTable=[real pred];
[EA,OA,AA,Kappa]=ClassifiEvaluate(MatrixClassTable);
disp('----------结果-------------')
disp('各类精度');EA
disp('总体精度');OA
disp('平均精度');AA
disp('kappa系数');Kappa
[real,n]=sort(real);
pred=pred(n);
figure;plot(real,'r*');
grid on;hold on;
plot(pred,'ko');
title(['分类正确率:',num2str(OA*100),'%'])
xlabel('测试集样本')
ylabel('标签')
legend('真实标签','预测标签')
function [temp3,OA,AA,Kappa]=ClassifiEvaluate(MatrixClassTable)
%求分类混淆矩阵ConfuMatrix
%MatrixClassTable为列的矩阵,第一列为目标类别,第二列为计算出的类别
MatrixClassTable=double(MatrixClassTable);
ClassNum=max(max(MatrixClassTable));
ConfuMatrix=zeros(ClassNum,ClassNum);
%混淆矩阵每行的和
RowSum=zeros(ClassNum,1);
%混淆矩阵每列的和
ColSum=zeros(1,ClassNum);
[Row,Col]=size(MatrixClassTable);
%计算混淆矩阵
for i=1:Row
ConfuMatrix(MatrixClassTable(i,1),MatrixClassTable(i,2))=ConfuMatrix(MatrixClassTable(i,1),MatrixClassTable(i,2))+1;
end
disp('混淆矩阵')
ConfuMatrix
%计算总体精度CorrectRate
%计算Kappa系数
for i=1:ClassNum
for j=1:ClassNum
RowSum(i,1)=RowSum(i,1)+ConfuMatrix(i,j);
ColSum(1,j)=ColSum(1,j)+ConfuMatrix(i,j);
end
end
%% 计算3种指标
temp1=0;
temp2=0;
temp3=[];
for i=1:ClassNum
temp1=temp1+ConfuMatrix(i,i);
temp2=temp2+RowSum(i,1)*ColSum(1,i);
end
for i=1:ClassNum
temp3=[temp3;ConfuMatrix(i,i)/sum(ConfuMatrix(i,:))];%各类精度
end
OA=temp1/Row;%总体精度 OA
Kappa=(Row*temp1-temp2)/(Row*Row-temp2);%KAPPA系数
AA=sum(temp3)/ClassNum;%平均精度 AA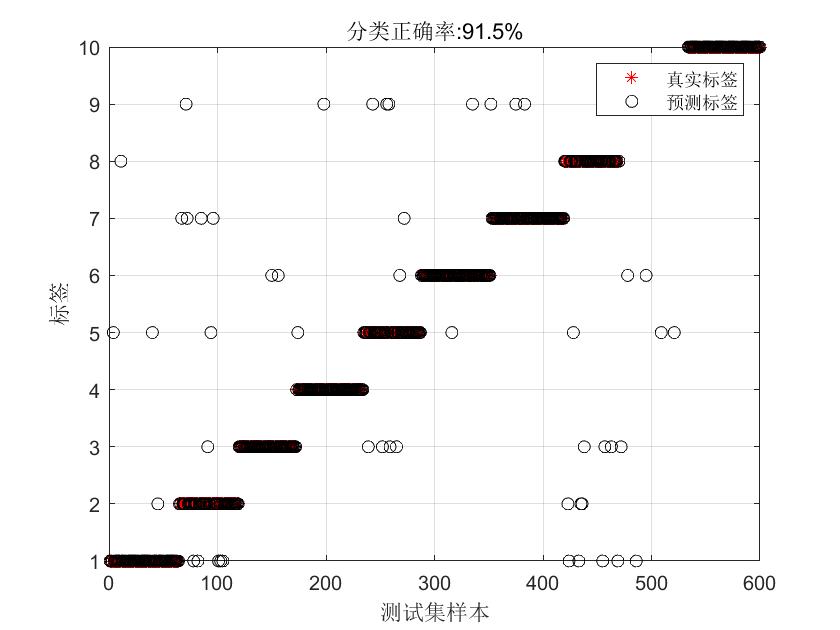
3.4 PCA降维+SDAE故障诊断
对训练集数据进行pca分析后,将数据降至600维,然后取训练集的参数对测试集也进行降维至600维度,最后利用降维后的数据进行SDAE建模。代码如下,测试集分类精度为93.83%。
%% 堆栈降噪自动编码器-PCA+SDAE用于轴承分类
clc;clear;close all;format compact
addpath(genpath('utils/'))
rng(0)
%% 1.导入数据
load result/data_process % data_original data_process
method=@mapminmax;%对数据进行标准化 #mapstd mapminmax、
[xs,mapping]=method(train_x');train_x=xs';
xts=method('apply',test_x',mapping);test_x=xts';
[pc,score,latent,tsquare] = pca(train_x);%我们这里需要他的pc和latent值做分析
tran=pc(:,1:600);
feature= bsxfun(@minus,train_x,mean(train_x,1));
feature_train_x= feature*tran;
feature= bsxfun(@minus,test_x,mean(train_x,1));
feature_test_x= feature*tran;
train_x=feature_train_x;
test_x=feature_test_x;
%% 网络训练
train_again=1;%#是否重新训练模型,不为1则调用之前保存的模型
if train_again==1
%% 无监督训练多个降噪自动编码器 假设输入维度为 sizes=[n n1 n2],则训练两个ae 一个是n-n1-n 一个是n1-n2-n1
sizes=[size(train_x,2) 50 30 size(train_y,2)]; % 这里 size(train_x,2)为输入层节点数 size(train_y,2)为分类层节点数
learningRate1=0.01;%各dae的学习率
denoise=0.5;%各dae的噪声强度
numepochs1=10;%各dae的训练次数
batchsize1=64;%%各dae的batchsize
activation_function='sigm';%各ae的激活函数
sae = sdaesetup(sizes,activation_function,learningRate1,denoise);
opts.numepochs = numepochs1;
opts.batchsize = batchsize1;
opts.show=0;% 0就不显示训练过程
disp('Train DAEs ')
sae = saetrain(sae, train_x, opts);
%% 构建一个多层前向网络,然后采用上面无监督预训练好的几个DAE的输入层-隐含层权重来初始化,这就叫堆栈降噪自编码器-SDAE
% 然后结合标签进行SDAE的微调训练
learningRate2=0.1;%sae的学习率
numepochs2=500;%sae的训练次数
batchsize2=64;%sae的batchsize
nn = nnsetup(sizes);%构建一个多层前向网络
nn.activation_function= 'sigm';%和上面保持一致
nn.learningRate= learningRate2;
nn=saeunfoldnn(nn,sae);%利用DAE的参数初始化SDAE
opts.numepochs = numepochs2;
opts.batchsize = batchsize2;
nn.output = 'softmax';
opts.show=0;% 0就不显示训练过程
opts.plot = 0;%0就不显示loss曲线
disp('Train SDAE ')
nn = nntrain(nn, train_x, train_y, opts);
disp('训练完毕')
save result/net5 nn
else
load result/net5
end
%% 预测 并计算指标
labels = nnpredict(nn, test_x);
[~, pred] = max(labels,[],2);
[~, real] = max(test_y,[],2);
%% 计算检测的正确率
MatrixClassTable=[real pred];
[EA,OA,AA,Kappa]=ClassifiEvaluate(MatrixClassTable);
disp('----------结果-------------')
disp('各类精度');EA
disp('总体精度');OA
disp('平均精度');AA
disp('kappa系数');Kappa
[real,n]=sort(real);
pred=pred(n);
figure;plot(real,'r*');
grid on;hold on;
plot(pred,'ko');
title(['分类正确率:',num2str(OA*100),'%'])
xlabel('测试集样本')
ylabel('标签')
legend('真实标签','预测标签')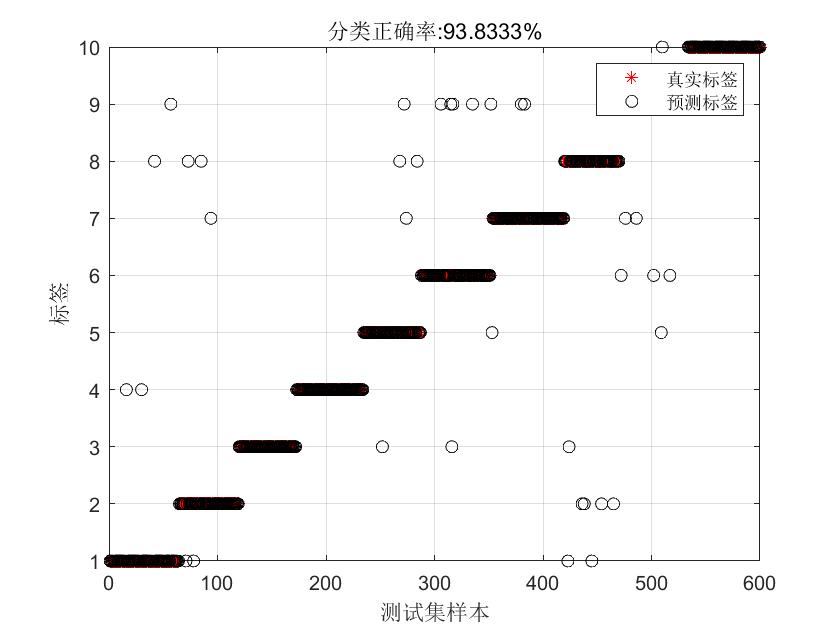
4 结语
更多内容请点击【专栏】获取。您的点赞是我更新【MATLAB神经网络1000个案例分析】的动力。博客中用到的数据集、工具箱都给了链接,程序也贴在博客中了,只需要稍微动动手就能跑出来,如果确实跑不来,可以在评论区找到打包好的文件。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










