前情回顾
1 题目
1.1 问题概述
目标:使用A*算法 or bfs、dfs算法,解决8数码问题。
八数码:是指在3x3的矩阵中,其中有8个格子放置成1-8,剩下一个格子是空格。你能够移动和空格相邻的格子到空格,直到这个矩阵满足每一行依次从左到右读取是有序,例如得到最后得到1-8有序,最后一个格子是空格。下图是一个例子:
使用广度优先搜索(BFS)和A*算法实现求解。
1.2 实现要求
- 实现一个Board类,存储每一个棋盘状态
- 存储棋盘状态
- 计算是否为最终解
- 查找邻近状态
- 计算与目标解间的距离(海明距离、曼哈顿距离)
- 计算代价函数(启发式得分)
- 输出唯一标识
- 实现一个Solver类,用于求解
- 求解
- 回溯并输出解
2 程序实现
2.1 Board类
class Board(object):
"""
data: NxN的二维数组,list or narray; 例如: np.array([[0,1,3],[4,2,5],[7,8,6]])
"""
def __init__(self, data, use_func = "hamming"):
if type(data) == list:
data = np.array(data)
self.board_data = data
self.use_func = use_func
self.prev = None
self.size()
# board size n
def size(self):
self.n = self.board_data.shape[0]
return self.n
# 从val值,得到其在八数码中的正确的问题。
def get_xy_from_value(self, val):
if val == 0:
return self.n-1,self.n-1
idx = (val) // self.n - 1
idy = (val) % self.n
return idx, idy
# 当前状态到目标状态的海明距离
def hamming(self):
dist = 0
for i in range(self.n):
for j in range(self.n):
if i==j==self.n-1:
break
if (i)*self.n+j+1 == self.board_data[i][j]:
pass
else:
dist += 1
return dist
# 当前状态到目标状态的曼哈顿距离
def manhattan(self):
dist = 0
for i in range(self.n):
for j in range(self.n):
if self.board_data[i][j] == 0:
continue
idx,idy = self.get_xy_from_value(self.board_data[i][j])
dist += abs(idx-i) + abs(idy-j)
return dist
# 启发式的得分 source
def get_score(self):
if self.use_func == 'hamming':
return self.height + self.hamming()
return self.height + self.manhattan()
# 是否是目标状态
def is_target(self):
if self.use_func == 'hamming':
return self.hamming() == 0
return self.manhattan() == 0
# 当前状态的所有邻居节点,return list<Board>
def neighbors(self):
all_neighbors = []
[zeroi,zeroj] = np.argwhere(self.board_data == 0)[0]
if zeroi < self.n - 1:
newdata = self.board_data.copy()
newdata[zeroi][zeroj], newdata[zeroi+1][zeroj] = newdata[zeroi+1][zeroj], newdata[zeroi][zeroj]
new = Board(newdata)
new.prev = self
all_neighbors.append(new)
if zeroj < self.n - 1:
newdata = self.board_data.copy()
newdata[zeroi][zeroj], newdata[zeroi][zeroj+1] = newdata[zeroi][zeroj+1], newdata[zeroi][zeroj]
new = Board(newdata)
new.prev = self
all_neighbors.append(new)
if zeroi > 0:
newdata = self.board_data.copy()
newdata[zeroi][zeroj], newdata[zeroi-1][zeroj] = newdata[zeroi-1][zeroj], newdata[zeroi][zeroj]
new = Board(newdata)
new.prev = self
all_neighbors.append(new)
if zeroj > 0:
newdata = self.board_data.copy()
newdata[zeroi][zeroj], newdata[zeroi][zeroj-1] = newdata[zeroi][zeroj-1], newdata[zeroi][zeroj]
new = Board(newdata)
new.prev = self
all_neighbors.append(new)
self.neighbor = all_neighbors
return all_neighbors
# 当前状态是否是最终状态 ?这个用来干啥的
def is_solvable(self):
return self.is_target()
# 棋牌状态的string表示,例如return "1 2 3 4 5 6 7 8 0"
def to_string(self):
data = self.board_data.flatten()
data = [str(each) for each in data]
return "_".join(data)
# 使用数值表示当前状态的唯一性,用于迭代过程中的判断
def hash_code(self):
hash_value = 0
for i in range(self.n):
for j in range(self.n):
hash_value = hash_value * 10 + self.board_data[i][j]
return hash_value
2.2 BFS和A*
BFS的实现,使用递归形式实现搜索,生成字符串存储查找集,并逐层传递(这里其实可以不用存储字典,会更节省内存)。当找到目标状态时,搜索结束并返回目标board。
由于目标board存储了上一步骤,因此可以回溯。
def BFS(queue, status, i = 0):
newqueue = []
for each in queue:
sta = each.to_string()
if sta in status.keys():
continue
#标记状态
status[sta] = each
each.height = i
if each.is_target():
return each,i
neighbors = each.neighbors()
newqueue.extend(neighbors)
i += 1
end,endi = BFS(newqueue, status, i)
return end,endi
A*只需要在此基础上,首先进行启发式函数的计算,并实现排序即可。
def Astar(queue, status, i = 0):
score = dict()
for each in queue:
each.height = i
if each.is_target():
return each
score[each] = each.get_score()
score = dict(sorted(score.items(), key=lambda d:d[1]))
newqueue = []
minscore = [each for each in score.values()]
for prior in score.keys():
if score[prior] > minscore[0]:
break
sta = prior.to_string()
if sta in status.keys():
continue
status[sta] = prior
neighbors = prior.neighbors()
newqueue.extend(neighbors)
i += 1
end = Astar(newqueue, status, i)
return end
2.3 Solver
class Solver(object):
"""
board:初始化棋盘状态。
use_algo: 解决八数码问题的算法,bfs和astart,当前你也可以实现dfs
"""
def __init__(self, board, use_algo="astar"):
self.board = board
self.ans_board = None
self.use_algo = use_algo
# 解决八数码问题,你必须实验这个函数,用来解决八数码问题
def solver(self):
if self.use_algo == "astar":
ans_board = Astar([self.board], dict(), i = 0)
else:
ans_board,endi = BFS([self.board], dict(), i = 0)
self.ans_board = ans_board
return ans_board
# 返回最短的路径
def moves(self):
return self.ans_board.height
# 返回最优结果的路径,你必须返回这个结果
def solution(self):
ans_list = []
last = self.ans_board
ans_list.append(last.board_data)
for i in range(self.ans_board.height):
last = last.prev
ans_list.append(last.board_data)
ans_list.reverse()
return ans_list
3 测试实现
3.1 本地测试
input[4x4]:
[[ 1 6 2 4]
[ 5 0 3 8]
[ 9 10 7 11]
[13 14 15 12]]
测试结果

input[3x3]:
[[0 1 3]
[4 2 5]
[7 8 6]]
测试结果
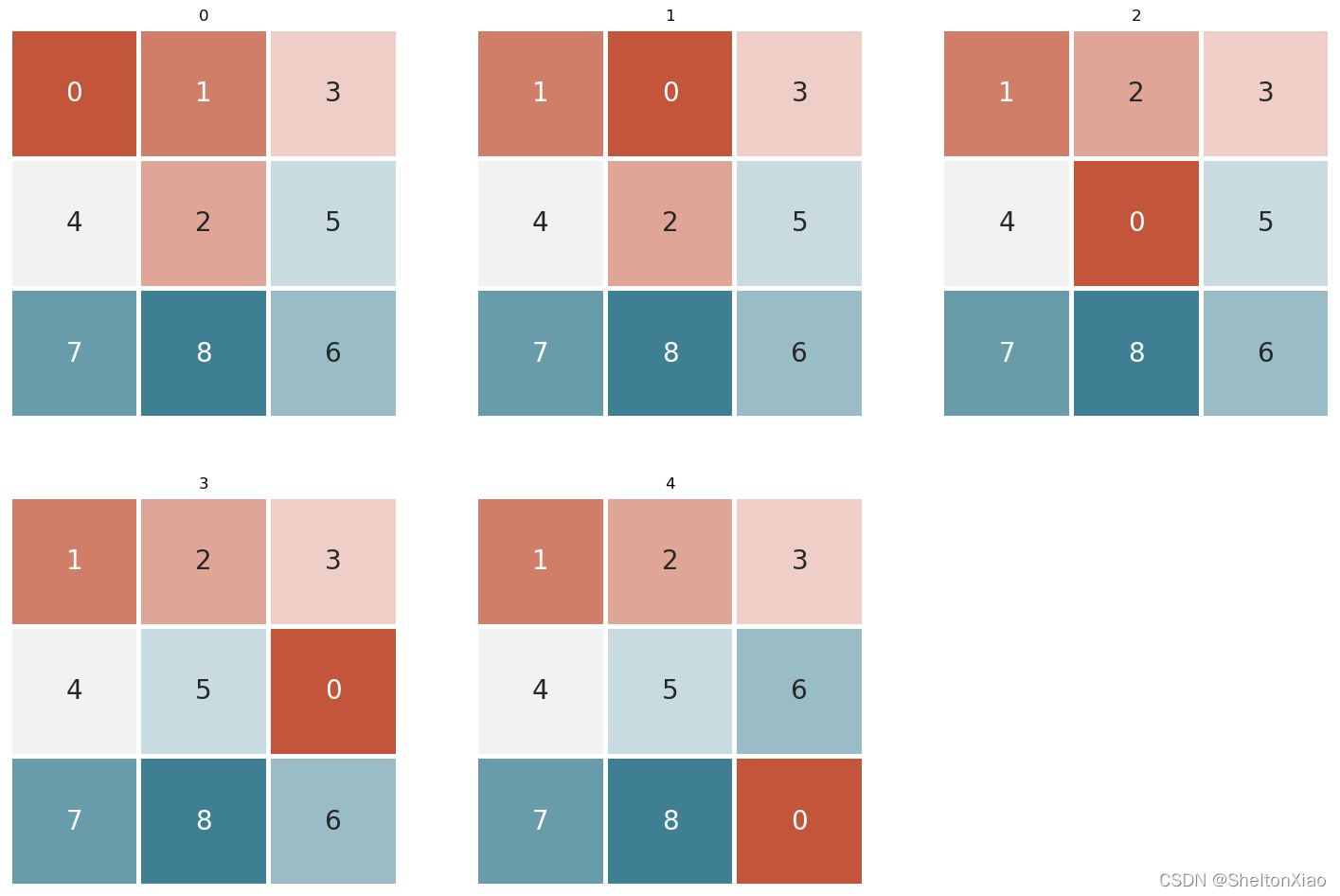
可视化代码如下
num = len(solution)
fig,ax = plt.subplots(num//3+1,3,figsize=(6*3, 6*(num//3+1)),dpi = 100)
for i in range(num):
each = solution[i]
sns.heatmap(each, cmap=sns.diverging_palette(20, 220, n=200), linewidths = 3,annot=True,cbar = False,annot_kws={"fontsize":20},ax = ax[i//3][i % 3])
ax[i//3][i % 3].set_title(str(i))
for i in range(ax.size):
ax[i//3][i % 3].axis("off")
3.2 线上测试
需要solver.solver()的返回值为列表,否则会报len的错误。
三阶数独

四阶数独
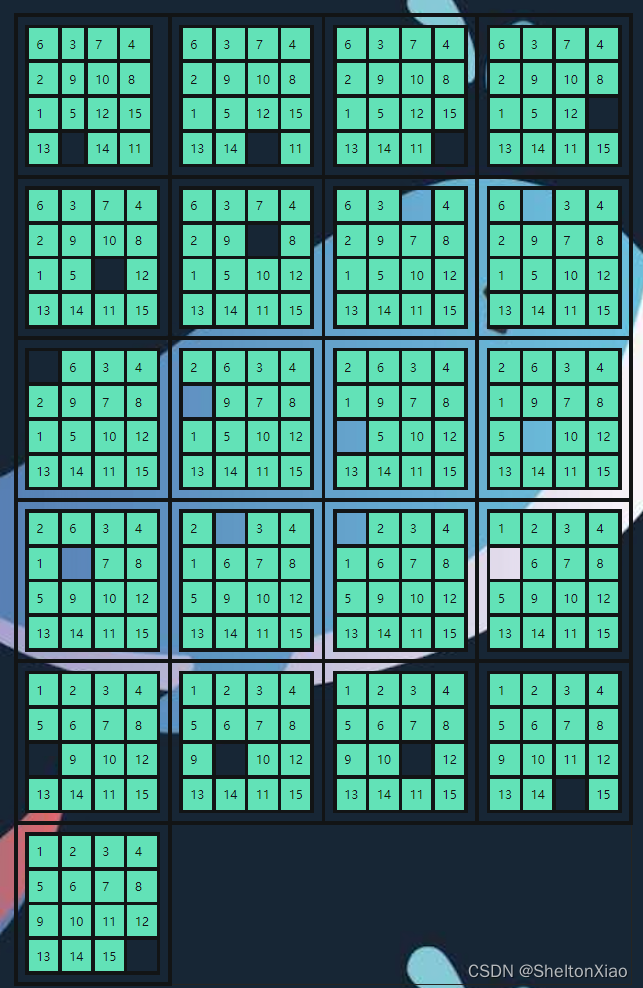
五阶数独





























 693
693

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










