P1005 矩阵取数游戏

最新推荐文章于 2022-09-17 17:18:18 发布

bnc1010

最新推荐文章于 2022-09-17 17:18:18 发布

阅读量309

点赞数

CC 4.0 BY-SA版权

分类专栏： dp

本文链接：https://blog.youkuaiyun.com/qq_40942372/article/details/85248197

dp 专栏收录该内容

31 篇文章

订阅专栏

本文介绍了解决洛谷P1005问题的一种方法，使用高精度动态规划来求解一个n*m矩阵在进行m次取数操作后的最大总权值。文章详细解释了如何独立处理每一行，通过枚举和状态转移方程来找到最优解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

链接：https://www.luogu.org/problemnew/show/P1005

题意：有一个n*m的矩阵。有m次取数操作，每次取数时，每行都要取出左边第一个或者右边第一个，有一个权值Vi等于取出的数*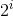 $2^{i}$ ，i为第几次取数。求总权值最大。

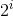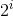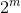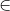思路：行与行之间没有相互影响，可以看作是独立的。对于一行，取左右两个端点l，r。dp[l][r]=max(dp[l-1][r]+num[][l-1]* $2^{i}$ ，dp[l][r+1]+num[][r+1]* $2^{i}$ )，这样的话，dp的终点是l=r的地方，枚举一下dp[x][x]+num[][x]* $2^{m}$ ,(x $\in$ [1,m])，最大值就是该行的最大贡献，加到答案中。n<=80，显然超过了long long范围，需要用高精度

Java参考代码：

import java.math.BigInteger;
import java.util.Scanner;

public class Main {

    public  static  BigInteger Max(BigInteger a, BigInteger b){
        if(a.compareTo(b) >= 0)return  a;
        else  return  b;
    }

    public static void main(String[] args){
        BigInteger [] er = new BigInteger[81];
        BigInteger tmp = new BigInteger("1");
        for (int i = 1; i <= 80; i++){
            tmp = tmp.multiply(new BigInteger("2"));
            er[i] = tmp;
        }
        tmp = new BigInteger("0");
        BigInteger [][] dp = new BigInteger[82][82];
        BigInteger [][] num = new BigInteger[82][82];
        Scanner cin = new Scanner(System.in);
        int n, m;
        n = cin.nextInt();
        m = cin.nextInt();
        for (int i = 1; i <= n; i++){
            for (int j = 1;j <= m; j++){
                num[i][j] = cin.nextBigInteger();
            }
        }
        for (int i = 1; i <= n; i++)num[i][0] = num[i][m+1] = tmp;

        int cnt = 0;
        BigInteger ans = new BigInteger("0");
        BigInteger tp = new BigInteger("0");

        for (int i = 1; i <= n; i++){
            for (int j = 0; j <= m; j++){
                for (int k = 0; k <= m+1; k++){
                    dp[j][k] = tmp;
                }
            }
            for (int j = 1; j <= m; j++){
                for (int k = m; k >= j; k--){
                    cnt = j - 1 + m - k;
                    if(cnt == 0)continue;
                    dp[j][k] = Max(dp[j-1][k].add(num[i][j-1].multiply(er[cnt])),dp[j][k+1].add(num[i][k+1].multiply(er[cnt])));
                }
            }
            tp = new BigInteger("0");
            for (int j = 1; j <= m; j++){
                tp = Max(tp, dp[j][j].add(num[i][j].multiply(er[m])));
            }
            ans = ans.add(tp);
        }
        System.out.println(ans);
    }
}