POJ1654(多边形面积）

小崔的技术博客

于 2020-03-05 21:25:42 发布

阅读量207

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/qq_40905284/article/details/104684421

本文介绍了一种计算由网格路径形成的多边形面积的方法，通过将输入的数字序列映射为坐标移动，最终形成封闭多边形，并利用向量叉乘计算其面积。面积结果为整数或0.5的倍数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：Area

题意：

在一个网格中,你当前在起始点,然后给你一些数字,每个数字表示你网当前位置的8个方向走一步.然后你到了下一个网格点了,就这样让你走出一个多边形,要你输出该多边形的面积. 题目保证最后一步是回到原点,且保证能形成多边形.

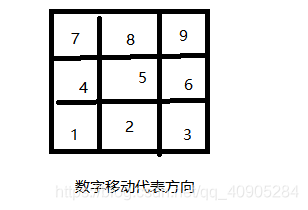
图示：

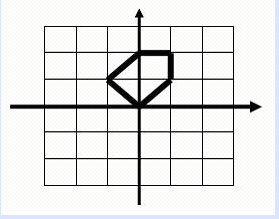
分析：

求的是多边形的面积，我们有求多边形面积的三角形法。首先我们将所有的点都找到，然后代入去计算就可以了。特点是这个面积要么是个整数，要么是0.5的倍数，所以可以先计算面积的俩倍，最后再来除。

Sample Input

Sample Output

代码：

#include <iostream>
#include <cstring>
#include <algorithm>


using namespace std;
const int N=1000010;

struct Point
{
	int x,y;
	Point(){
	}
	Point(int x,int y):x(x),y(y){
	}
	
 } ;
 
 typedef Point Vector;
 
 Vector operator - (Point A,Point B)
 {
 	return Vector(A.x-B.x,A.y-B.y);
 }
 
 long long Cross(Vector A,Vector B)
 {
 	return A.x*B.y-A.y*B.x;
 }
 
 long long PolygonArea(Point *p,int n)
 {
 	long long area=0;
 	for(int i=1;i<n-1;i++)
 		area+=Cross(p[i]-p[0],p[i+1]-p[0]);
 		
 	return area<0?-area:area;
 }
 
 const int dx[]={0,-1,0,1,-1,0,1,-1,0,1}; //将数值映射成坐标 
 const int dy[]={0,-1,-1,-1,0,0,0,1,1,1};
 
 char str[N];
 Point p[N];
 
 int n;
 int main()
 {
 	int T;
 	scanf("%d",&T);
 	while(T--)
 	{
 		n=0;
 		p[0]=Point(0,0);
 		scanf("%s",str);
 		n=strlen(str)-1; //最后一个5没用
		
		for(int i=0;i<n-1;i++)
			p[i+1]=Point(p[i].x+dx[str[i]-'0'],p[i].y+dy[str[i]-'0']);
			
		long long ans=PolygonArea(p,n);
		if(ans%2==0) printf("%d\n",ans/2);
		else printf("%d.5\n",ans/2);
 		
	 }
 }