1509. 【普及模拟】单元格

题目描述

在一个R行C列的表格里，我们要选出3个不同的单元格。但要满足如下的两个条件：

（1）选中的任意两个单元格都不在同一行。

（2）选中的任意两个单元格都不在同一列。

假设我们选中的单元格分别是：A，B，C，那么我们定义这种选择的“费用”= f[A][B] + f[B][C] + f[C][A]。 其中f[A][B]是指单元格A到单元格B的距离，即两个单元格所在行编号的差的绝对值 + 两个单元格所在列编号的差的绝对值。例如：单元格A在第3行第2列，单元格B在第5行第1列，那么f[A][B] = |3-5| + |2-1| = 2 + 1 = 3。至于f[B][C], f[C][A]的意义也是同样的道理。现在你的任务是：有多少种不同的选择方案，使得“费用”不小于给定的数minT，而且不大于给定的数maxT，即“费用”在【minT, maxT】范围内有多少种不同的选择方案。答案模1000000007。所谓的两种不同方案是指：只要它们选中的单元格有一个不同，就认为是不同的方案。

样例

输入样例	3 3 1 20000	3 3 4 7	4 6 9 12	7 5 13 18	4000 4000 4000 14000
输出样例	6	0	264	1212	859690013

分析 (我没有盗图)

             

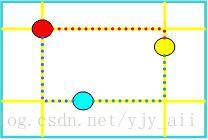
首先可以先开一个脑洞，想像一个大正方形被切割很多个矩形。

such as（s），一个4x4的正方形可以分割成16个1x1的小正方形，12个1x2的小长方形......

然后再仔细观察上图，发现其实这三个点之间的距离相加就是这个矩形的周长-4,。

那么我们就可以枚举这个矩形的长和宽了，然后在算这个小矩形在我们大矩形（R，C）中出现的次数就可以了。那么这个矩形在大矩形的出现的次数即为（R - r + 1）（C - c + 1）。r和c为我们枚举的小矩形。

接着，我们需要判定这个矩形的周长-4是否满足：mint <= 2(i + j) - 4 <= maxt。

两种情况：

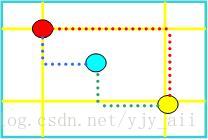
1.三点都在边上，有一点在顶点

2.三点都在边上，有两点在顶点 

（这也是为什么要想像我们有很多小矩形的原因，我们要尽量计算点在边上或顶点的情况）

1情况：有(i−2)(j−2)可能 // -2是因为顶点不算 

2.情况：有(i−2)(j−2)可能 // -2是因为顶点不算 

然后我们可以发现，这种情况是可以有变化的，某个在顶点上的点如果位置变化那么情况又会随之变化。

那么经过交换顶点后：

1情况：有4* (i−2)(j−2)种可能

2情况：有2* (i−2)(j−2)种可能

共有6 * 2(i−2)(j−2)种可能。 

在综合就有：6 * 2(i-2)(j-2) * (R - r + 1) *（Ｃ－ｃ＋１）

Ｃｏｄｅ

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
long long n,m,mint,maxt,ans = 0;
int main()
{
	freopen("table.in","r",stdin);
	freopen("table.out","w",stdout);
	scanf("%lld %lld %lld %lld",&n,&m,&mint,&maxt);
	for(register long long i = 3;i <= n;++i)
		for(register long long j = 3;j <= m;++j)
			if(mint <= 2 * j + 2 * i - 4 && 2 * j + 2 * i - 4 <= maxt)
			{
				ans += 6*(i-2)*(j-2)*(n-i+1)*(m-j+1);
				ans = ans % 1000000007;
			}
	printf("%lld",ans);
	return 0;
}