C程序-蓝桥-历届试题 买不到的数目

问题描述

小明开了一家糖果店。他别出心裁：把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。

小朋友来买糖的时候，他就用这两种包装来组合。当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。

你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。

本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。

输入格式

两个正整数，表示每种包装中糖的颗数(都不多于1000)

输出格式

一个正整数，表示最大不能买到的糖数

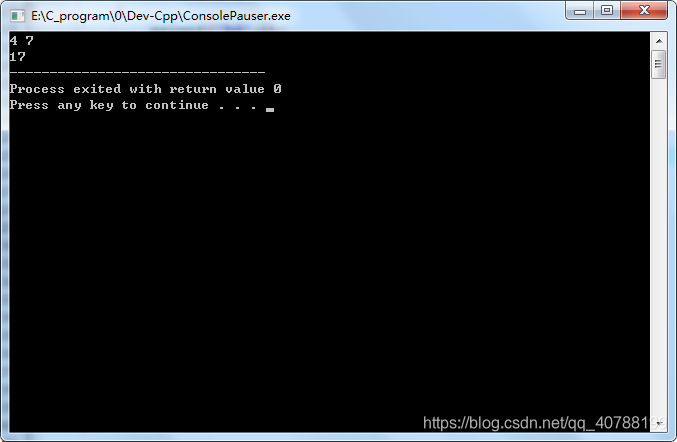
样例输入1

4 7

样例输出1

17

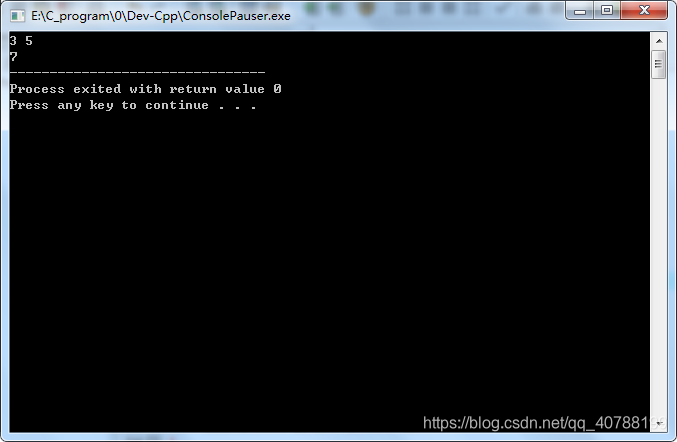
样例输入2

3 5

样例输出2

7

 思路分析：最小公倍数以上的数肯定能凑出来，所以从最小公倍数往小查找，当（c-i*a）%b=0即仍是可以凑出来的，第一个出现的即是最大的。

#include <iostream>
#include <stdio.h>

int gcd(int a,int b);
int solve(int a,int b,int c);

int main( ) 
{
	int a,b,c,t;
	scanf("%d%d",&a,&b);
	
	c=a*b/gcd(b,a);//c是最小公倍数 
	
	for(int i=c-1;i>0;i--)//从最小公倍数小1的数开始查找 
	{
		if(solve(a,b,i))
		{
			printf("%d",i);
			break;
		}
	}
	return 0;
}

int gcd(int a,int b)//求最大公约数 
{
	if(b==0)
		return a;
	else 
		return gcd(b,a%b);
}

int solve(int a,int b,int c)
{
	while(c>0)//(c-i*a)%b=0即可以凑出来 
	{
		if(c%b==0||c%a==0)//整除，说明能凑出来 
			return 0;
		c=c-a;//c-b也行，a>b,可以减少循环次数 
	}
	
	return 1;//不能凑出来 
}