关于贪心算法的一些介绍

贪心算法核心思想

1.局部最优解得到整体最优解

这个就写个遍历就行了，比较简单。



区间按照结尾进行排序。

贪心算法，永远尽可能多的不断贪心的选取当前最优策略的算法。

贪心的核心在于可以用小的替换大的，不能替换的时候就不可以用贪心算法了。


问的是最多最多有介个孩子可以得到满足
孩子要尽可能多
所以我们应该用糖果去找孩子
看看我这个糖果能满足的最小的孩子是是谁



子序列，本序列中删除一些数据之后剩下已然成立就是子序列。
摇摆序列说穿了就是，先升，后降低，然后再升，再降低
上面题目中，后面该降低了，所以选最大那个数15比较容易降低

在一段递增序列中，根据取舍，递增之后就是下降了，为了有更大下降空降，我们必须要在取舍时候，将递增序列中最大那个值需要的结果

在一段递减序列中同理为了递增我们也要选择最小那个值作为下将的取舍
其实这个题目，数那个折现就行了，每次都找波峰和波谷
然后数折就行了
最后那个折数量 + 1就是我们要的子序列的长度。

class Solution {
    public int wiggleMaxLength(int[] nums) {
        if(nums.length < 2){
            return nums.length;
        }

        //子序列可以不是连续的，原本序列中删除一些元素之后也叫子序列
        //因为中间可以跳过一些点

        //用count去统计那些点可以组成子摇摆序列
        //
        //作为判定上升还是下将依据，上升之后就该下降了
       

        //两个指针去遍历数组，pre ,next
        int pre = 0;
        int next = 1;
        int isUp;//1就是上升，0就是下降
        int isNow;//表示这一次是上升还是下降
        //看看前面有没有转折
        isUp = nums[pre] > nums[next] ? 0 : 1;//记录一下一开始是上升还是下
        int count = 1;//计算发生了多少次转折
        //两个指针放心往后走就行，发生转折就记录下来

        while(next < nums.length){
            isNow = nums[pre] > nums[next] ? 0 : 1;//记录一下一开始是上升还是下
            
            //相等时候不用处理
            //不相等时候才发生转折
            if(isUp != isNow){
                //说明发生了转折
                count++;//记录一次转折
                isUp = isNow;//isUp变化一下
            }
            pre++;
            next++;//无论如何指针都往后走

            
           

        }

        return count + 1;//统计节点数目



    }
}

class Solution {
    public int wiggleMaxLength(int[] nums) {
int down = 1, up = 1;
    for (int i = 1; i < nums.length; i++) {
        if (nums[i] > nums[i - 1])
            up = down + 1;
        else if (nums[i] < nums[i - 1])
            down = up + 1;
    }
    return nums.length == 0 ? 0 : Math.max(down, up);

    }
}

神级别代码

一个贪心题目

这个跳跃游戏最大的点就是在于，我每次追求的事情是
num[i] + i最大，我当年犯的错误就是仅仅是追求num[i]值，最大

class Solution {
    public int jump(int[] nums) {
        int end = 0;
    int maxPosition = 0; 
    int steps = 0;
    for(int i = 0; i < nums.length - 1; i++){
        //找能跳的最远的
        maxPosition = Math.max(maxPosition, nums[i] + i); //将每一个点可以跳跃最远的下标都记录了，
        //然后遇到end点，就会根据我的记录进行更新，每一个点可以跳跃的最短下标，都没记录可。相当于记录每一个点的潜力
        //每次遇到end就推进一下潜力，
        //我当年犯下的最大错误就是，应该是 i + nums[i]最大，而不是仅仅是nums[i]最大，这才是最贪心的地方
        //我们的目的是将nums[i] + i进行推进
        if( i == end){ //遇到边界，就更新边界，并且步数加一
            end = maxPosition;
            steps++;
        }
    }
    return steps;

    }
}

这就是贪心算法。局部最优解，换取整体最优解。

class Solution {
public:
string minNumber(vector& nums) {
// 选择排序
int len = nums.size();
vector ans;
for (auto num : nums){
ans.push_back(to_string(num));
}

    for (int i = 0; i < len; i++){
        int minIndex = i;
        for (int j = i + 1; j < len; j++){
            if (ans[minIndex] + ans[j] > ans[j] + ans[minIndex]){
                minIndex = j;
            }
        }

        string temp = ans[minIndex];
        ans[minIndex] = ans[i];
        ans[i] = temp;
    }

    string ret = "";
    for (auto str : ans){
        ret += str;
    }
    
    return ret;
}

};

作者：Dormiveglia_Zachary
链接：https://leetcode.cn/problems/ba-shu-zu-pai-cheng-zui-xiao-de-shu-lcof/solution/by-dormiveglia_zachary-5dqj/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

加油站问题，首先，当加的油小于行程闭环时候，说明这个点根本不会是起点，因为都不够到下一站。

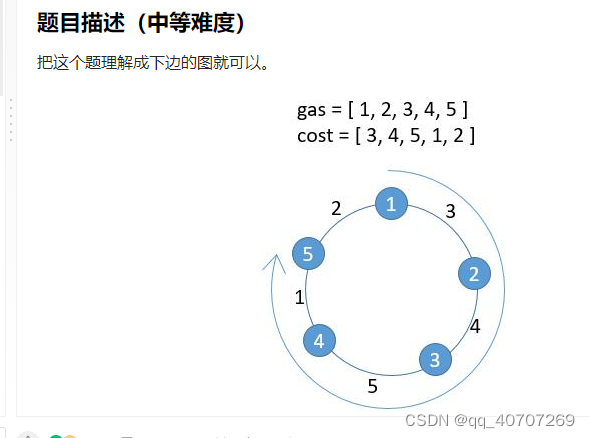
1.首先我们可以建立一个数组
gas - cost数组
如果整个数组之和小于0，那么无论如何你都是跑步玩的
同时新数组里，负数一定不会是起点。

最好理解的解决方式：

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int n = gas.length;
        int sum = 0;
        for(int i = 0;i < n;i++){
            sum += gas[i] - cost[i];
        }

        if(sum < 0){
            return -1;
        }

        int currentGas = 0;
        int start = 0;
        for(int i = 0;i < n;i++){
            currentGas += gas[i] - cost[i];
            if(currentGas < 0){
                currentGas = 0;
                //相当于遍历所有节点，不断计算当前油量
                //如果剩余油量小于0，那么说明起始节点到当前节点之间不存在解决问题的点。
                //那么就需要重新洗牌，重新从下一个节点开始
                start = i + 1;
            }
        }
        return start;
    }
}

详细刷题视频合集 本题视频讲解
刷题笔记

思路：首先判断总油量是否小于总油耗，如果是则肯定不能走一圈。如果否，那肯定能跑一圈。接下来就是循环数组，从第一个站开始，计算每一站剩余的油量，如果油量为负了，就以这个站为起点从新计算。如果到达某一个点为负，说明起点到这个点中间的所有站点都不能到达该点。
复杂度：时间复杂度O(n)，空间复杂度O(1)

原理就是当到达你这个点时候，别人只有三种状态，要么有油或者没油，没油到不了你这里，能到你这，要么有油要么为0，若是为0那么和从你这里作为起点一模一样，如果有油的状态下，从你这里都跑不到重点，那么从你这里作为起点更不可能了。

 public String minNumber(int[] nums) {
        String[] strs = new String[nums.length];

        for (int i = 0; i < nums.length; i++) {
            strs[i] = String.valueOf(nums[i]);
        }

        for (int i = 0; i < strs.length; i++) {
            for (int j = 0; j < strs.length - 1; j++) {
                // 比如 34,3 -----> 343 > 334 所以两个数需要交换位置
                if ((strs[j] + strs[j + 1]).compareTo(strs[j + 1] + strs[j]) > 0) {
                    String tmp = strs[j + 1];
                    strs[j + 1] = strs[j];
                    strs[j] = tmp;
                }
            }
        }

        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < strs.length; i++) {
            sb.append(strs[i]);
        }
        return sb.toString();
    }

作者：bu-zheng-jing-de-pgrammer
链接：https://leetcode.cn/problems/ba-shu-zu-pai-cheng-zui-xiao-de-shu-lcof/solution/wei-shi-yao-ta-shi-yi-ge-pai-xu-wen-ti-b-hh21/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

用冒泡排序去解决问题

问题的关键就是我们使用字符串进行数据对比
字符串A + B表示一个数字
字符串B + A表示一个数字

A在左边 B在右边
如果A + B大于B + A
最左边应该组合后更小数字
如果A + B大于B + A那么我们就要交换A,B之间位置

31

这个题难度的点在于，我们需要去重，但是同时也要保证值

实际上对于值
a b d b d c a
来说，我在去重的同时还要保证不重复
什么样的情况下，我要去除掉前面重复的数字呢？
那么就是，前面重复的数字比后面的数字大，并且，前面重复的数字后面还会出现
比如d …a …d
满足的条件就是
首先d是重复的，并且d比后面的数字要大

class Solution {
    public String removeDuplicateLetters(String s) {

        //先遍历所有值，放进一个HashMap里面，
        Map<Character,Integer> map = new HashMap<>();
        //key是值，v是重复次数1
        char[] str = s.toCharArray();
        
        //用一个set维持前面已经有数据,已经有的值就不往里面装了
        HashSet<Character> set = new HashSet<Character>();
        for(char c : str){
            map.put(c,map.getOrDefault(c,0) + 1);


        }
        //用一个Linkelist，因为双向链表，两边都能弹出

        LinkedList<Character> resultlist = new LinkedList<>();

        //利用LinkedList的peeklast功能对比最后一位
        for(char c : str){
            
                //插入之前里面要套一层循环
                while(true){

                    //设计思路
                    //如果为null了，直接跳出循环

                    //一个字符，如果小于前面的那一位，并且前面那一位后面还有
                    //并且我自己这一位前面没有再出现就加入，否则跳出循环
                    if(resultlist.isEmpty()){
                        break;
                    }
                    
                     char Ischar = resultlist.peekLast();
                    //判断一下最后一位和即将插入的谁大
                    if(Ischar > c && map.get(Ischar) > 0 && !set.contains(c)){
                        //并且钱前面没有我这个值
                        //满足前面两个条件，并且前面没有我
                        //我比将要进来那个大，并且后面还有
                        resultlist.pollLast();
                       
                        //同时更新set表
                        set.remove(Ischar);
                    }else{
                        //如果最后一位并不比将插入的值大，并且后面还有，那么直接插入就完了
                        //跳出循环
                        break;
                    }

                }
               
            //还有个去重呢
            if(!set.contains(c)){
                resultlist.add(c);//无论如何这个c一定要进入
                set.add(c);
                //当我们将某一位加入之后，那么被加入的那个也会影响hash表
                //更新hash表
                

            }


            map.put(c,map.get(c) - 1);//只要被遍历过，就要再hash表中去掉重复次数,不要再前面进行重复处理了
            
        }

        //如果最后一位是ASII码比要加入的AASII码大，并且最后一位再后面还会出现

        //那么就是可以弹出去的


        //最后将链表转化为String
        StringBuilder sb = new StringBuilder();
        for(char c : resultlist){
            sb.append(c);
        }
        return sb.toString();
        

    }
}

处理的关键点
1.一个hash表记录每个字母重复次数
2.字母被遍历过之后，记得更新hash表
3.用一个set记录当前有哪些值在list里
4.记得经常更新set
5.增加一个字母，记得要用循环，因为它可能一口气干掉钱前面n多字母
6.删除一个字母之后，并不需要更新记录次数的hash，因为这个字母被用过次数就会减少。

621任务调度器

方法(贪心算法)
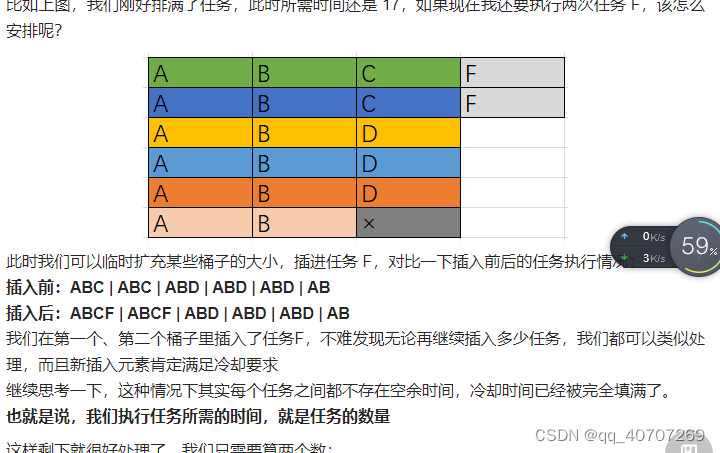
容易想到的一种贪心策略为：先安排出现次数最多的任务，让这个任务两次执行的时间间隔正好为n。再在这个时间间隔内填充其他的任务。

例如：tasks = [“A”,“A”,“A”,“B”,“B”,“B”], n = 2

我们先安排出现次数最多的任务"A",并且让两次执行"A"的时间间隔为2。在这个时间间隔内，我们用其他任务类型去填充，又因为其他任务类型只有"B"一个，不够填充2的时间间隔，因此额外需要一个冷却时间间隔。具体安排如下图所示：

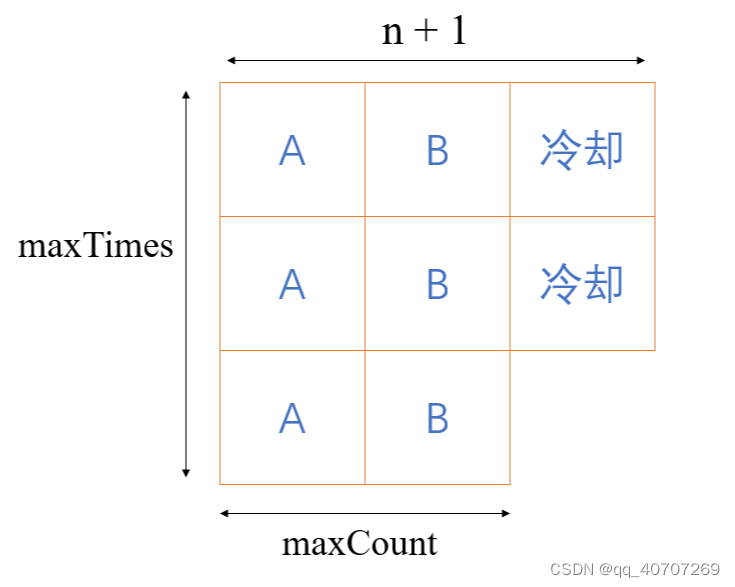
其中，maxTimes为出现次数最多的那个任务出现的次数。maxCount为一共有多少个任务和出现最多的那个任务出现次数一样。

图中一共占用的方格即为完成所有任务需要的时间，即：

(maxTimes - 1)*(n + 1) + maxCount
(maxTimes−1)∗(n+1)+maxCount

此外，如果任务种类很多，在安排时无需冷却时间，只需要在一个任务的两次出现间填充其他任务，然后从左到右从上到下依次执行即可，由于每一个任务占用一个时间单位，我们又正正好好地使用了tasks中的所有任务，而且我们只使用tasks中的任务来占用方格（没用冷却时间）。因此这种情况下，所需要的时间即为tasks的长度。

由于这种情况时再用上述公式计算会得到一个不正确且偏小的结果，因此，我们只需把公式计算的结果和tasks的长度取最大即为最终结果。

先安排重复次数最多的数组，这样效率比较高。

我们先统计一下所有数据的重复次数
使用数组进行排序

这个题的贪心基础理论是
1.先排重复次数多的那个
，然后让重复次数少的数据往重复次数多的里插入，因为重复次数少交替插入，比较好插入

这样的话，重复次数最多那个数字，势必无论如何都会占用

如果在这个各自范围内我们将别的都插入进来，那么就完美了

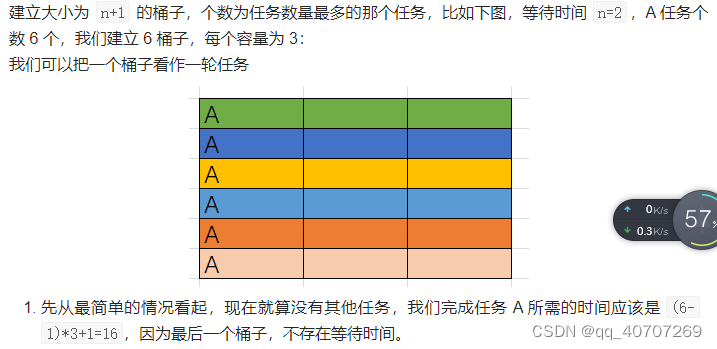
这个代价是无论如何都要付出的

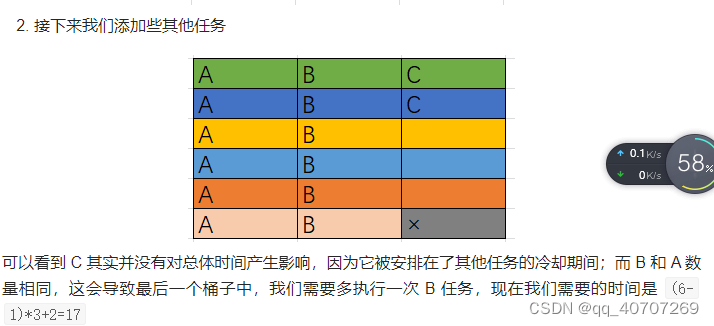
由于等待N位置的原则。原则上，每个位置上数据只能出现一次
每个行只能放一个数据

435

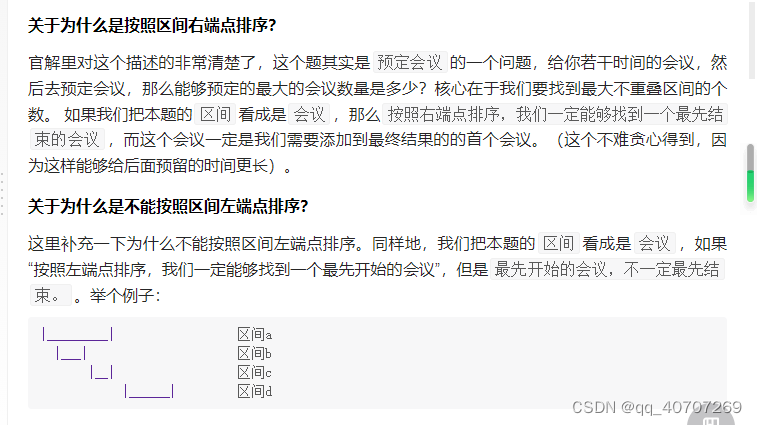
直接按结束时间进行排位，因为结束时间，靠前开始时间整体来说会比较靠前，我们可以根据结束时间判断，和别人的开始时间会不会重叠了。

406. 根据身高重建队列

我们要确定两个维度的东西

思路
本题有两个维度，h和k，看到这种题目一定要想如何确定一个维度，然后在按照另一个维度重新排列。

其实如果大家认真做了135. 分发糖果，就会发现和此题有点点的像。

在135. 分发糖果我就强调过一次，遇到两个维度权衡的时候，一定要先确定一个维度，再确定另一个维度。

如果两个维度一起考虑一定会顾此失彼。

对于本题相信大家困惑的点是先确定k还是先确定h呢，也就是究竟先按h排序呢，还先按照k排序呢？

如果按照k来从小到大排序，排完之后，会发现k的排列并不符合条件，身高也不符合条件，两个维度哪一个都没确定下来。

那么按照身高h来排序呢，身高一定是从大到小排（身高相同的话则k小的站前面），让高个子在前面。

此时我们可以确定一个维度了，就是身高，前面的节点一定都比本节点高！

那么只需要按照k为下标重新插入队列就可以了，为什么呢？

以图中{5,2} 为例：

!406.根据身高重建队列

按照身高排序之后，优先按身高高的people的k来插入，后序插入节点也不会影响前面已经插入的节点，最终按照k的规则完成了队列。

所以在按照身高从大到小排序后：

局部最优：优先按身高高的people的k来插入。插入操作过后的people满足队列属性

全局最优：最后都做完插入操作，整个队列满足题目队列属性

局部最优可推出全局最优，找不出反例，那就试试贪心。

一些同学可能也会疑惑，你怎么知道局部最优就可以推出全局最优呢？ 有数学证明么？

在贪心系列开篇词关于贪心算法，你该了解这些！中，我已经讲过了这个问题了。

刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心，至于严格的数学证明，就不在讨论范围内了。

如果没有读过关于贪心算法，你该了解这些！的同学建议读一下，相信对贪心就有初步的了解了。

回归本题，整个插入过程如下：

排序完的people： [[7,0], [7,1], [6,1], [5,0], [5,2]，[4,4]]

插入的过程： 插入[7,0]：[[7,0]] 插入[7,1]：[[7,0],[7,1]] 插入[6,1]：[[7,0],[6,1],[7,1]] 插入[5,0]：[[5,0],[7,0],[6,1],[7,1]] 插入[5,2]：[[5,0],[7,0],[5,2],[6,1],[7,1]] 插入[4,4]：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]

此时就按照题目的要求完成了重新排列。

简单来说就是，我们维持住一个，队列，
然后遍历所有排好序的前面的数组
数组中，根据第二个数字，也就是自己排名情况，去安插数据。前面，我们最起码可以知道，已经在队列中的数字，的high高度一定是比我高的，这样直接往里面插就完了，根据自己的第二位，也就是下标直接往队列是根据下标插就行了。

整个队列里，所有值都是高于我的，根据我的下标插入，是合理的。

解题思路
先按照身高H从高到低排序，矮的人放在后面，这样在排队时不会对前面已经排好的队伍产生影响（因为数组中记录的是身高大于等于自己的人，身高小于自己的不管放在自己前面和后面都不会有影响）；
如果有身高相同的人，那么就要按照K从小到大排序，因为K小的肯定会排在K大的前面（具体原因可以用反证法来证明：假设有[hi, ki], [hj, kj]，且hi=hj,ki<kj，如果hj在hi的前面，那么ki>=kj+1成立，+1的原因是hi前面有hj。 => 矛盾，假设不成立，hi肯定在hj的前面）。

作者：yimeixiaobai
链接：https://leetcode.cn/problems/queue-reconstruction-by-height/solution/gen-ju-shen-gao-zhong-jian-dui-lie-ren-h-oynb/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

135

分发糖果的题目

简单来说，就是每个人一开始分到一个糖果
我们需要建立一个新的数组，数组和每个人得分顺序是一一映射的。
然后从前往后，遍历得分数组，如果后面的比前面的数字大，那么映射数组里，必然会后面的糖果数量是前面糖果数量 + 1.这样可以很好的满足，左规则。

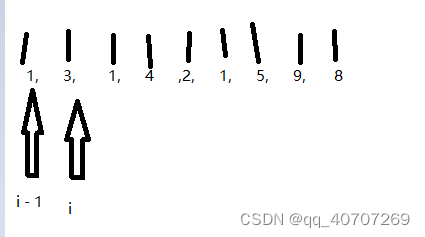
从左向右遍历，代表左规则。
只要i > i - 1那么，就是满足左规则的，那么 i对应的数值，就要比i + 1对应的数值大

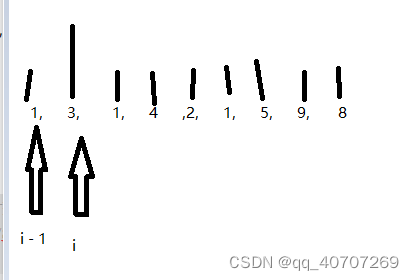
一直遍历到最后，说明满足左规则。

但是此时，是不一定满足右规则的。
那么，我们还要把数组从右边往左再次遍历，一次，如果前面的，比后面的大，那么，前面的
会是后面的糖果数量+ 1
a[j] = a[j+1] + 1

这里有个很有趣的细节，就是数组最后一位，最后一位是不需要满足右规则的，因为右边啥也没有。

最后一位，最终，就是左数组最后一位的大小。

在满足右规则的情况下，我们还要考虑是不是满足左规则，这个时候，就需要进行类比
与满足左规则的数组进行对比，更大那个值，可以同时满足两个规则。

class Solution {
    public int candy(int[] ratings) {
        int[] left = new int[ratings.length];
        int[] right = new int[ratings.length];
        Arrays.fill(left, 1);
        Arrays.fill(right, 1);
        for(int i = 1; i < ratings.length; i++)
            if(ratings[i] > ratings[i - 1]) left[i] = left[i - 1] + 1;
        int count = left[ratings.length - 1];
        for(int i = ratings.length - 2; i >= 0; i--) {
            if(ratings[i] > ratings[i + 1]) right[i] = right[i + 1] + 1;
            count += Math.max(left[i], right[i]);
        }
        return count;
    }
}

作者：jyd
链接：https://leetcode.cn/problems/candy/solution/candy-cong-zuo-zhi-you-cong-you-zhi-zuo-qu-zui-da-/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

我自己写的，我们可以从头到尾只折腾一个序列

class Solution {
    public int candy(int[] ratings) {
        int[] line = new int[ratings.length];
        
        Arrays.fill(line, 1);

        for(int i = 1; i < ratings.length; i++)
            if(ratings[i] > ratings[i - 1]) line[i] = line[i - 1] + 1;
        int count = line[ratings.length - 1];
        for(int i = ratings.length - 2; i >= 0; i--) {
            if(ratings[i] > ratings[i + 1]){
                line[i] = Math.max(line[i + 1] + 1,line[i]);


            }
          
            count += line[i];
        }
        return count;
    }
}