回溯算法fsdafasd

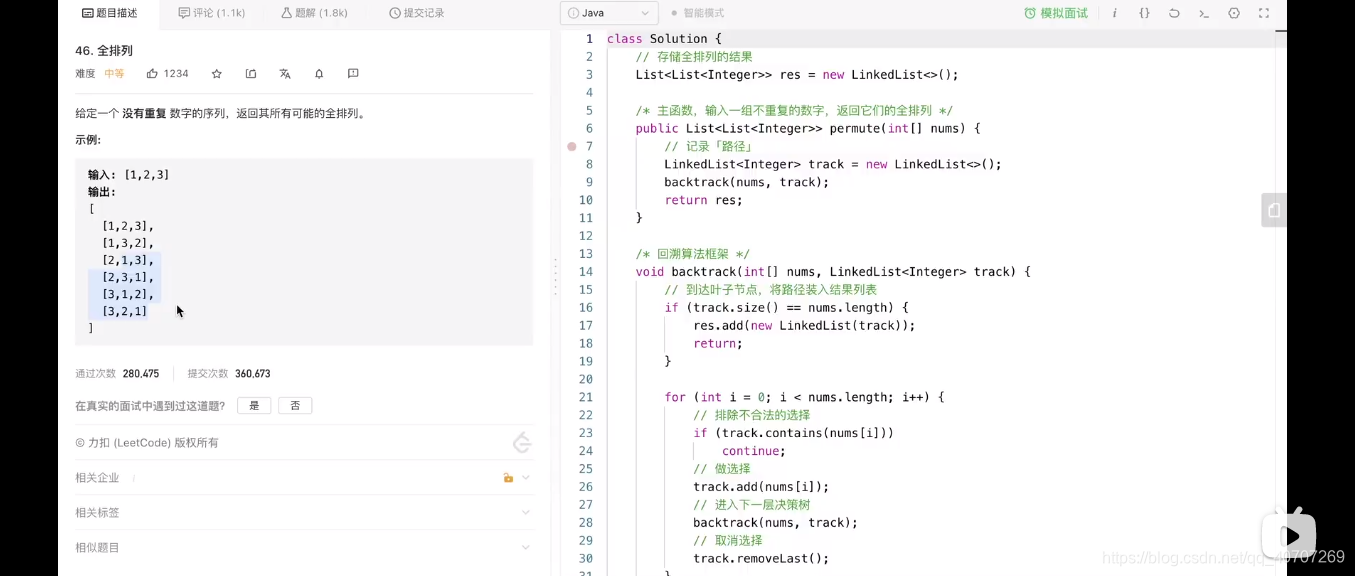
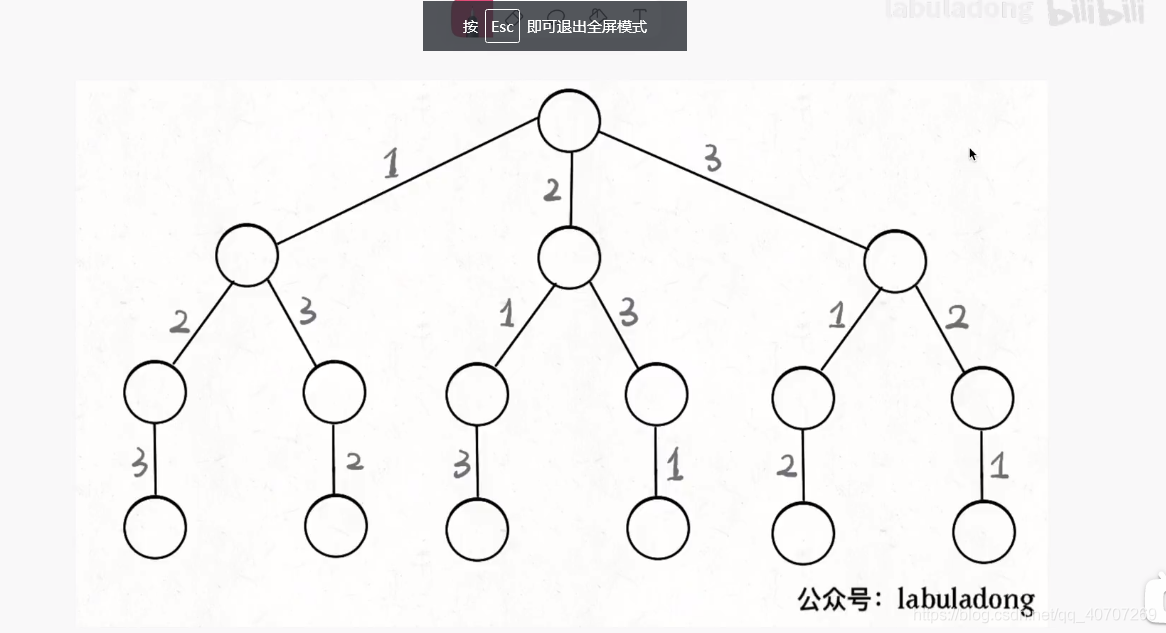
将题目转化为递归树的问题。


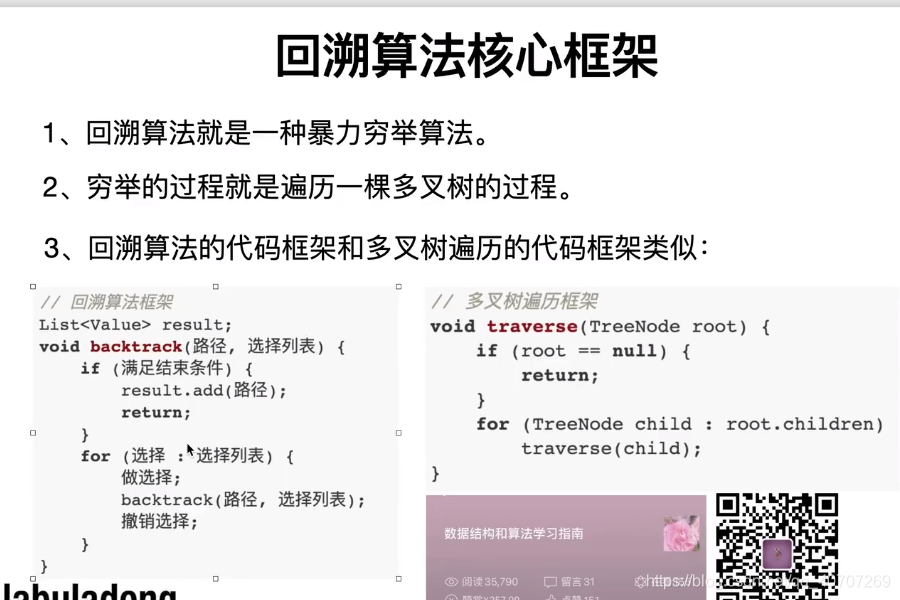
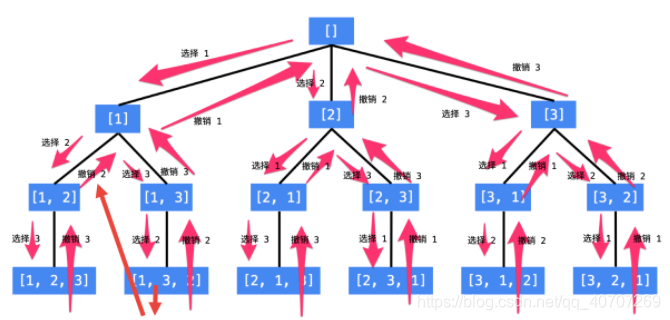
用一个List装载回溯的值，当一个回溯到达底层时候，用一个List去装载回溯的值，每次重新回溯的时候都要注意，当你重新回溯时候，一定一定要把List中值取消掉，也就是说回溯算法需要取消掉自己的操作。

1.步骤，用一个List<List> res装载返回值
用一个List跟着节点去遍历，遍历成功后，将路径值加进去，当到底的时候，也就是list值等于数组长度时候，到底了。到底就记得要回溯
回溯和递归回去有一个本质区别‘
就像月光宝盒一样，你必须撤除自己做过的操作。’

回溯算法的本质是题目让我们找全所有解法。


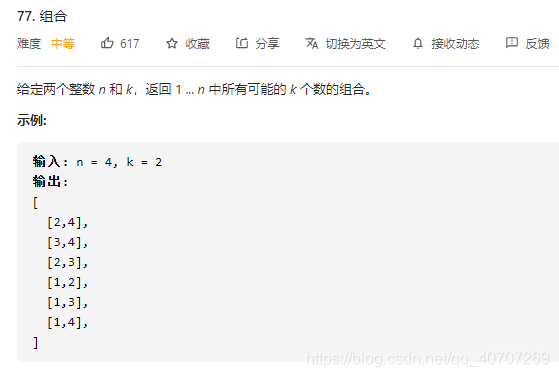
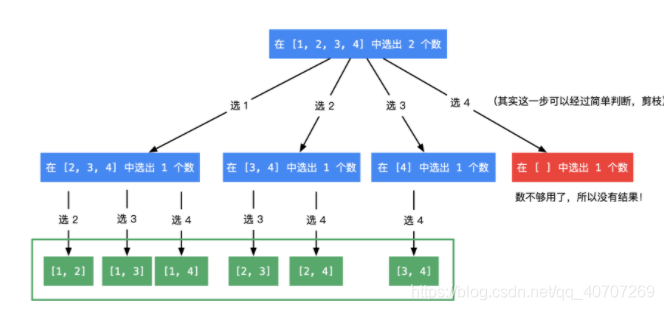
每次传递数值时候把数组传递进去就行了，然后控制一下start和end
记住比自己小的值不能传递进去。
每次传递这个数组就行了

本质就是递归加遍历，在每一层数组中多次调用递归，多次进行遍历。

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        //前面的数不能大于后面的数
        //用一个List<List<Integer>>返回数
        int[] num = new int[n];
        for(int i = 0;i < n;i++){
            num[i] = i + 1;
        }
        List<List<Integer>> res = new ArrayList<>();
        //用来存数值
        LinkedList<Integer> path = new LinkedList<>();//返回中间值
        for(int i = 0;i < num.length;i++){//从这里就是多重递归，开始递归之旅
            dfs(num,res,i,path,k);
            path.pollLast();

        }
        
        return res;


    }

    //不需要返回值，每次都传递res和path就行

    public void dfs(int[] num,List<List<Integer>> res,int start,LinkedList<Integer> path,int k){
        path.add(num[start]);//进了循环就将数据加入路径
        //我们用一个对象传递数据，所以不用担心返回值问题
        //返回终止条件
        if(path.size() == k){
            //路径值大小等于K返回
            res.add(new LinkedList(path));//将path的值放进去，不能放地址，这步相当于复制了path的值
            return;
        }

        for(int i = start;i < num.length - 1;i++){
            //回溯算法是递归和循环相结合
        
            dfs(num,res,i + 1,path,k);
            path.pollLast();//把尾巴弹出来撤销自己上次的选择
        }
    }
}

我这个方法，可以做，但是很蠢逼，相当于
在主函数里搞了个for循环遍历
在dfs子函数里也搞了个for循环遍历，全都是因为一个问题
那就是在一进dfs时候，就把当前节点加入路径了，这样
这个for循环就影响不到节点加入路径这个问题了。
正确降低代码量的方式应该是，将path.add()这个操作放到for循环里去，这样第一次操作时候{1,2,3,4}整个数组都会被作为选择。

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        //前面的数不能大于后面的数
        //用一个List<List<Integer>>返回数
        int[] num = new int[n];
        for(int i = 0;i < n;i++){
            num[i] = i + 1;
        }
        List<List<Integer>> res = new ArrayList<>();
        //用来存数值
        LinkedList<Integer> path = new LinkedList<>();//返回中间值
        
            dfs(num,res,0,path,k);
            


        
        return res;


    }

    //不需要返回值，每次都传递res和path就行

    public void dfs(int[] num,List<List<Integer>> res,int start,LinkedList<Integer> path,int k){
        
        //我们用一个对象传递数据，所以不用担心返回值问题
        //返回终止条件
        if(path.size() == k){
            //路径值大小等于K返回
            res.add(new LinkedList(path));//将path的值放进去，不能放地址，这步相当于复制了path的值
            return;
        }

        for(int i = start;i < num.length;i++){
            //回溯算法是递归和循环相结合
            path.add(num[i]);//进了循环就将数据加入路径
        
            dfs(num,res,i + 1,path,k);
            path.pollLast();//把尾巴弹出来撤销自己上次的选择
        }
    }
}

//一道很标准的回溯题目

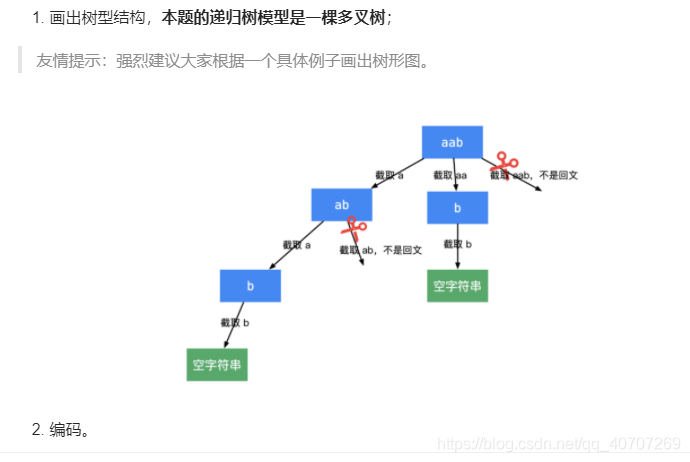
实际上关键点就是两个
1.截取字符串之后判断劫走的部分是不是回文？是的话加入路径
2.从剩下的部分中继续劫走，当遇到空字符串时候全部路径返回
3.两个函数，一个用来回溯，另一个用来判断是不是回文字符串。

22

标准回溯算法


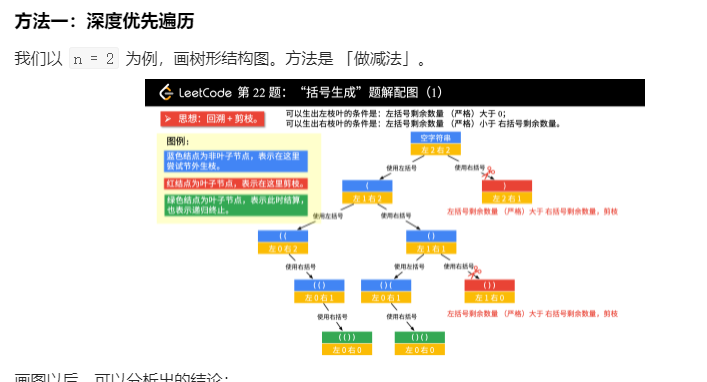
n = ?实际上就是告诉了你左边和右边括号数量
两个数组一个放左括号，一个放右边括号，然后去递归

当做括号数量小于等于右括号时候，向左递归，减少左括号数量是正确的
当右括号数量少于左括号时候，这个递归丧失任何意义。
//因为无法匹配

class Solution {
    public List<String> generateParenthesis(int n) {
        //这种题目必然回溯算法
        //用一个栈存储路径，当路径错误时候直接返回
        //当左边n不为n-1 不为零时候，可以一直向左递归
        int left = n,right = n;
        //
        List<String> res = new ArrayList<>();
        //作为返回值
        String path = new String();//直接用String,根本不用回溯
        //路径进行拍徘徊

        dfs(res,path,left,right);
        return res;





        

    }

    public void dfs(List<String> res,String path, int left,int right ){
        if(left == 0 && right == 0){
            //括号全部被耗尽
            res.add(path);//将字符串存进去
            return;
            
        }

        

       //无论如何都可以向左递归
       if(left - 1 >= 0){
           //只要下面的值比0大就可以往左回溯
           //左边为0都没关系，还有右边呢
              
                dfs(res,path + '(',left - 1,right);
                //递归回来之后记得恢复状态
               
       }
   
    


//如果减去1之后大于等于左边
         if(right - 1 >= left && right - 1 >= 0){
            //可以向右递归
            
                dfs(res,path + ')',left,right - 1);
                //递归回来之后记得恢复状态
                
                //将string转化为StringBuilder

        }





    }
}

直接用STring根本不用回溯。

17

回溯题目


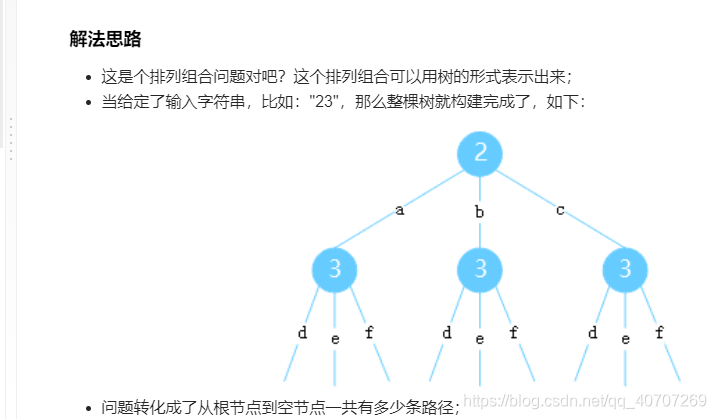
依然可以转化为类似这种无数路径的题目

class Solution {
    public List<String> letterCombinations(String digits) {

        //我们从这里只能采用分割的方式拿到数据，分割的话拿到的都是数字的字符
        //所以我们必须在创建对应的表的时候，使用字符对应字符串方式，存储
        List<String> result = new ArrayList<>();//用于返回结果
        if(digits.length() == 0){
            return result;//为0则直接返回
        }

        Map<Character,String> letterMap = new HashMap<>(){{
            put('2', "abc");
            put('3', "def");
            put('4', "ghi");
            put('5', "jkl");
            put('6', "mno");
            put('7', "pqrs");
            put('8', "tuv");
            put('9', "wxyz");
           }};
           //将字符对应的映射放在这里

           backtrack(digits,letterMap,result,0,new StringBuffer());
           //需要一个index索引随时表示我们应该处理哪一个digits下标准
           return result;



    }


    public static void backtrack(String digits,Map<Character,String> letterMap,List<String> result,int index,StringBuffer path){

        if(path.length() == digits.length()){
            //到达标准了
            result.add(path.toString());
            //将字符串放进去
            return;

        }

//StringBuffer的delete功能
        //如果没到的话，随和是
        String letter = letterMap.get(digits.charAt(index));//获取那个字符串
        //然后开启递归模式
        for(int i = 0;i < letter.length();i++){
            //StringBuffer是可以进行回溯的
            path.append(letter.charAt(i));//加上这个字符串路径中
           backtrack(digits,letterMap,result,index + 1,path);//接着去进行递归
           //递归回来后，Index还是那个东西，我们值需要将path的数据进行回溯就行了
           path.deleteCharAt(path.length() - 1);//完成回溯
           //这里不能用i因为i比较大
        }

        

    }
}

90

这个题目讲了回溯的本质

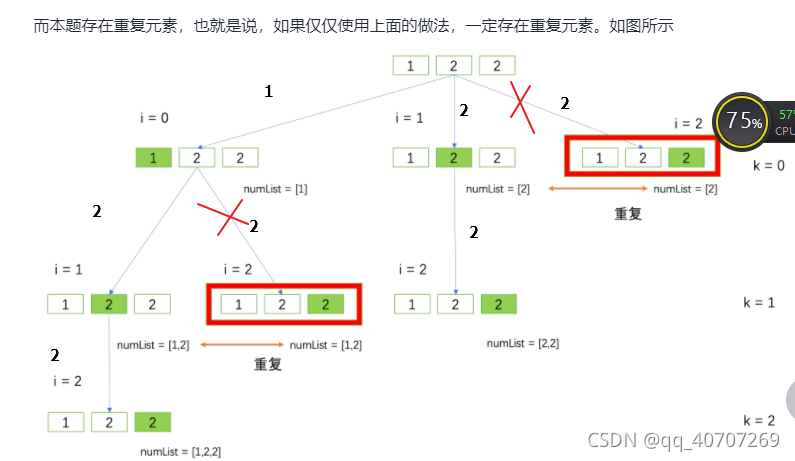
可以看出来同一层一旦出现连续相同数字，就会让整体开始重复，下一层重复是没关系的
毕竟1,2,2也是我们需要的答案
最重要的就是同一层重复的，只能访问一次。
那么对Nums进行排序，将所有都放在一起
在递归的每一层都去记录这层这个数据有没有被访问过，重要的是切断每一层之间的联系。同一层之间不要访问，相同的元素。但是下一层可以访问相同元素。

class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {

        Arrays.sort(nums);
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> numList = new ArrayList<>();

        dfs(nums,res, numList, 0);

        return res;
    }

    private void dfs(int[] nums,List<List<Integer>> res,List<Integer> numList,int k){

        res.add(new ArrayList(numList));

        Map<Integer,Boolean> visited = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            visited.put(nums[i], false);
        }

        for (int i = k; i < nums.length; i++) {
            if(!visited.get(nums[i])){
                numList.add(nums[i]);
                dfs(nums, res, numList,i+1);
                numList.remove(numList.size()-1);
                visited.put(nums[i], true);
            }
        }
        
    }
}

作者：LeegouHai
链接：https://leetcode-cn.com/problems/subsets-ii/solution/tu-jie-chao-xiang-xi-fen-xi-hui-su-fa-ja-h4ry/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

38

关键点是，我们必须标记一下，被访问过的元素，然后每次都是从头开始遍历，遇到访问过的元素，必须错过去，让循环继续，才能将所有没有访问过的元素都集中起来。

class Solution {
     public String[] permutation(String s) {

        HashSet<String> set = new HashSet<>();
        char[] c = s.toCharArray();//进行访问

        //需要一个数组证明z已经被访问过了
        boolean[] vis = new boolean[10];//证明已经访问过了
        StringBuilder sb = new StringBuilder();
        Arrays.fill(vis,false);
        dfs(set,c,sb,vis);

        //将set拿出来当成数组
        String[]  result = new String[set.size()];

        int idx = 0;//用来往里面放
        for(String str : set){
            result[idx++] = str;
        }

        return result;
    }


    //传递进来一个StringBuilder,传进来一个字符串数组，传递进来一个set，一个访问数组
    public void dfs(HashSet<String> set, char[]  c, StringBuilder s, boolean[] vis){

        //返回的情况是
        if(s.length() == c.length){
            set.add(s.toString());//就给变成String
            return;//直接返回了
        }

        //如果没存满，接着遍历
        for(int i = 0;i < c.length;i++){
            if(!vis[i]){
                s.append(c[i]);//直接加进来
                //随后标记一下i
                vis[i] = true;//标记为已经读了
                //不然就接着往下走
                dfs(set,c,s,vis);
                s.deleteCharAt(s.length() - 1);//移除自己最后一位
                vis[i] = false;//移除自己所有的操作


            }
            else{

                //关键就是这一步
                //我们每次都是从头开始遍历的，访问没有访问过的元素，所以遇到已经被访问过的元素
                //你必须过掉，让循环可以走进下一个，让循环可以访问下一个元素
                continue;//如果当前这个已经被访问过了，你必须去看后面那个，当前这个就过去了
            }

        }

    }
}

https://leetcode.cn/problems/zi-fu-chuan-de-pai-lie-lcof/solution/gong-shui-san-xie-tong-yong-shi-xian-qu-4jbkj/