基于MHSS的ARAIM算法的详细分析解释

北航_Curry

已于 2022-03-12 21:19:50 修改

阅读量3.7k

点赞数 13

分类专栏：卫星导航文章标签：卫星导航 ARAIM RAIM 完好性卫星故障检测与排除 1024程序员节

于 2021-10-13 22:27:08 首次发布

本文链接：https://blog.youkuaiyun.com/qq_40643699/article/details/120742728

版权

卫星导航专栏收录该内容

7 篇文章

订阅专栏

RAIM和ARAIM的区别

完好性支持信息ISM

地面监测网通过观测核心星座，生成能反映核心星座固有性能的参数( 完好性支持信息 ( Integrity Support Message ，ISM) ) ，并发送给载接收机。ISM主要给出的是卫星导航系统的具有极高可靠性的安全判定信息。 ISM 主要包括：

用户测距误差（User Range Error, URE）：用来计算精度和连续性的标称误差高斯分布的标准差；
用户测距精度（ User Range Accuracy, URA ）：用来计算完好性的标称误差高斯分布的标准差；
卫星故障率 P sat ，星座故障率 P const ；（这些都是先验概率）
连续性偏差（ b nom ）：估计精度和连续性的标准状况下典型偏差大小；
完好性偏差（ b max） $b_{nom,i}$ ：用于无故障条件下完好性评估的最大偏差；

所有需要监测的故障模式（子集）的确定

MHSS 算法监测的故障情况包含 :

1) 一颗卫星发生故障。

2) 一个星座发生故障。

3) 上述 2 种情况任意数量的组合。

故障数指某个故障模式下（也就是某个子集下）发生故障的卫星/星座数。
对于卫星故障或者星座故障，统称为事件，总的卫星数记为 $N_{sat}$ ，总的星座数记作 $N_{const}$ ，那么总的事件数 $N_{event}=N_{sat}+N_{const}$
每一种故障模式可以理解为不同的事件组合而成的

这一段是我自己的理解：

因为我们如果考虑可能出现的最大故障数越大，那么子集的数量就越大。但是故障数越大时，就代表其发生概率很低，几乎可以不用去考虑这种情况的发生。因此我们定义了一个最大故障数 $N_{fault,max}$ .

最大故障数 $N_{fault,max}$ 的计算方法：

MHSS多假设解分离算法

什么是子集？

即全可见星集合中排除掉某颗或某几颗卫星的卫星集合。

MHSS的基本原理

全可见星解为使用全可见星集合定位的结果，子集解为子集卫星定位的结果。算法认为，在无故障情况下，全可见星解和所有的子集解应聚集一起。而如果某颗卫星存在故障，则使用该故障卫星测量值的全可见星定位解和子集定位解将产生偏移，不含故障卫星的子集定位解将更接近飞机实际位置。通过对比各个子集解和全可见星解的距离即可判断是否存在故障。

若所有子集解距离全可见解小于预设阈值，则认为无故障存在，若有子集解的距离超出阈值，则认为存在故障。从而采用排除算法，实现故障卫星的移除，最后确保至少有一组子集是由全部无故障卫星组成的。

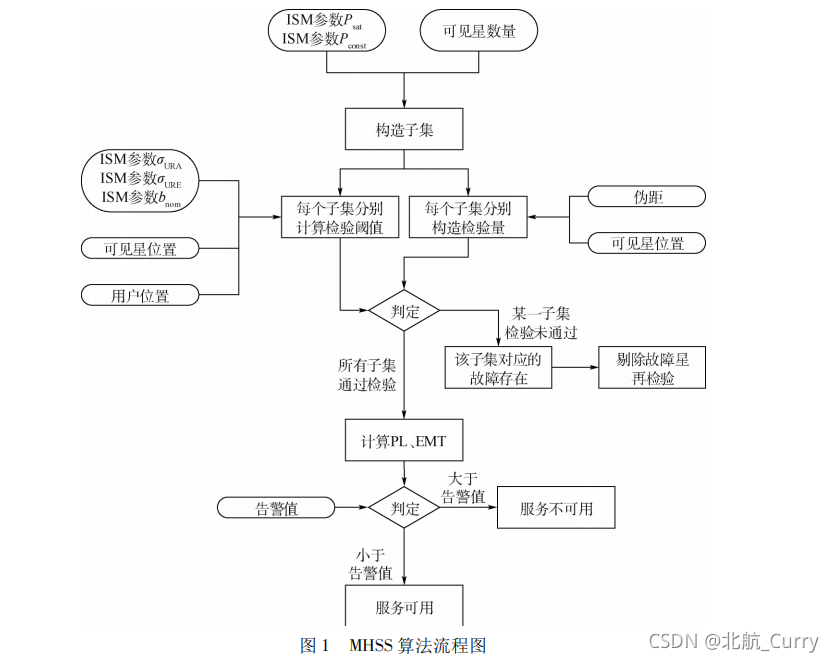
机载接收机运行 MHSS 算法，把接收到的卫星信号和 ISM 作为输入，判断卫星或星座是否故障，有故障排除故障; 无故障计算保护级等，判断服务是否可用。（保护级是在无故障情况下算的，有故障时计算的保护级无意义，因为计算出来的也是错误的）

MHSS算法公式推导

线性化伪距观测方程 $y=Gx+\varepsilon$ 的推导

设可见星的个数为n，可得以下n几个方程:

$\rho _{1}=\sqrt{(x_{1}-x_{0})^{^{2}}+(y_{1}-y_{0})^{^{2}}+(z_{1}-z_{0})^{^{2}}}+ct_{u}$

$\rho _{2}=\sqrt{(x_{2}-x_{0})^{^{2}}+(y_{2}-y_{0})^{^{2}}+(z_{2}-z_{0})^{^{2}}}+ct_{u}$

..............

$\rho _{n}=\sqrt{(x_{n}-x_{0})^{^{2}}+(y_{n}-y_{0})^{^{2}}+(z_{n}-z_{0})^{^{2}}}+ct_{u}$ 1

其中 $(x_{0},y_{0},z_{0})$ 为用户接收机的位置坐标，属于未知量，也是本方程组想要计算的量， $(x_{i},y_{i},z_{i}) , i\subset (1,n)$ 为n颗可见性的位置坐标（可从卫星星历计算得到）， $ct_{u}$ 为各个卫星钟差导致的伪距偏差（属于误差项，也是未知因素）， $\rho _{i}$ 是通过卫星和接收机时钟乘以光速可计算得出的已知量。

由上面的公式，根据最小二乘法可以计算 $(x_{0},y_{0},z_{0},t_{u})$ 的解—— $(x\hat{}_{0},y\hat{}_{0},z\hat{}_{0},t\hat{}_{u})$ , 即 $(x_{0},y_{0},z_{0},t_{u})$ 的估计值。（真实值是计算得不到的，只能计算一个估计值）（本文中上面带有尖号的量都是估计量）

得到 $(x_{0},y_{0},z_{0},t_{u})$ 后，重新构建以下n个方程：

$\rho\hat{} _{i}=\sqrt{(x_{i}-x\hat{}_{0})^{^{2}}+(y_{i}-y\hat{}_{0})^{^{2}}+(z_{i}-z\hat{}_{0})^{^{2}}}+ct\hat{}_{u}$ $i\subset (1,n)$ 2

公式2可以这么理解，通过公式1的计算， = 右边的都是已知量了，从而可以计算出一个 $\rho\hat{} _{i}$ 。 $\rho\hat{} _{i}$ 是通过估计的用户接收机坐标计算到的每一颗可见星的伪距。

定义

$\Delta \rho _{i}=\rho\hat{} _{i}-\rho _{i}$ ，即真实伪距与伪距估计值之差

$(\Delta x_{0},\Delta y_{0},\Delta z_{0},\Delta t_{u})$ = $(x\hat{}_{0},y\hat{}_{0},z\hat{}_{0},t\hat{}_{u})-(x_{0},y_{0},z_{0},t_{u})$ 即接收机真实左边减去估计坐标

上面两个都是误差量，属于未知量，我们假设无故障情况下他们都是高斯分布。

根据上面的定义，公式2可以改写成：

$\rho _{i}+\Delta \rho_{i} =\pounds (x\hat{}_{0},y\hat{}_{0},z\hat{}_{0},t\hat{}_{u})=\pounds (x_{0}+\Delta x_{0},y_{0}+\Delta y_{0},z_{0}+\Delta z_{0},t_{u}+\Delta t_{u})$ 3

将公式3进行傅里叶展开，得到n个方程组：

$\Delta \rho _{i} = -\frac{x_{i}-x\hat{}_{i}}{r_{i}}\Delta x_{0}-\frac{y_{i}-y\hat{}_{i}}{r_{i}}\Delta y_{0}-\frac{z_{i}-z\hat{}_{i}}{r_{i}}\Delta z_{0}+c\Delta t_{u}$

$r_{i}=\sqrt{(x_{i}-x\hat{}_{0})^{2}+(y_{i}-y\hat{}_{0})^{2}+(z_{i}-z\hat{}_{0})^{2}}$ 4

公式4用矩阵形式描述为：

$\begin{bmatrix} \Delta \rho _{1} \\ \Delta \rho _{2} \\ ... \\ \Delta \rho _{n} \end{bmatrix}= G \begin{bmatrix}\Delta x _{0} \\ \Delta y _{0} \\ \Delta z _{0} \\c \Delta t _{u} \end{bmatrix}$ 5

公式5即为：

$y=Gx+\varepsilon$ 6

其中， $\varepsilon$ 为测量误差矢量；G为观测矩阵，由接收机与卫星间方向余弦及接收机钟差相关系数组成；y为观测矩阵与线性化伪距预测值之间的差值；x 表示接收机三维位置及时钟与标称值的偏差。

y、x、 $\varepsilon$ 都认为是服从高斯分布。

公式6可以理解为伪距观测误差和接收机位置误差相联系起来的方程。

故障识别算法推导

利用最小二乘法，可获得n颗可视卫星下的接收机坐标的估计值 $p\hat{_{0}}$ :

$p\hat{_{0}}$ = $(G^{T}W_{URA}G)^{-1}G^{T}W_{URA}y=S_{0}y$ 7

$p\hat{_{0}}$ = $(x\hat{}_{0},y\hat{}_{0},z\hat{}_{0},t\hat{}_{u})$

公式7中， $S_{0}$ 为无故障假设下加权最小二乘投影矩阵，可以理解为把 y 投影成 $x\hat{_{0}}$ （这个y的含义还不明确）；
$W_{URA}$ 为n×n的加权对角矩阵（只有对角线有元素），其对角线元素是URA的函数， $W_{URA}$ = $(C_{int})^{-1}$ ， $C_{int}$ 为完好性标称误差对角协方差矩阵，其计算方法如下所示：

$C_{int}(k, k) = \sigma _{URA,k}^{2}+ \sigma _{tropo,k}^{2}+ \sigma _{user,k}^{2}$ 8

$C_{int}$ 同样也是只有对角线有元素
$\sigma _{URA,k}^{2}$ 是用于完好性的星历星钟误差的标准差，这个我觉得可以从完好性支持信息ISM的用户测距精度（User Range Accuracy, URA）计算得来
$\sigma _{tropo,k}^{2}$ 和 $\sigma _{user,k}^{2}$ 分别是对流层延迟误差和接收机噪声误差。（这个我觉得也是通过一些给定信息计算而来）

相应地，可以获得排除第k颗卫星条件下接收机坐标的估计 $p\hat{_{k}}$ ：

$p\hat{}_{k}=(G^{T}M_{k}W_{URA}G)^{-1}G^{T}M_{k}W_{URA}y=S_{k}y$ 9

$M_{k}$ 为第k个对角元素置零的n×n维单位矩阵；

因此，第 k 颗卫星的检验统计量如下：

$d_{k}=\left | p\hat{} _{k}-p\hat{} _{0}\right |$ 10

每一颗卫星都有自己的检验统计量，用于检验是否有故障

检测门限如下：

$D_{k}=K_{fa,k}\times \sigma _{d,k}+\sum_{i=1}^{N}\left | \Delta S_{k}(3,i) \right |\times b_{nom,i}$ 11

$\Delta S_{k}=S_{k}-S_{0}$ ，这里的Sk和S0在公式7、9中，后面的（3，i）我觉得是第三行第i列的意思
$\sigma _{d,k}$ 为垂直方向第 k 颗卫星的检验统计量 ݀ $d_{k}^{}$ 的标准差， $\sigma _{d,k}=\sqrt{dP_{k}(3,3)}$ ， $dP_{k}=\Delta S_{k}W_{URE}^{-1}\Delta S_{k}^{T}$ ，其中 $W_{URE}$ 是n×n的加权对角阵，其对角线元素是URE的函数， $W_{URE}$ $=(C_{acc})^{-1}$ ， $C_{acc}$ 为用于精度和连续性的标称误差对角协方差矩阵，其计算方法如下所示： $C_{acc}(k, k) = \sigma _{URE,k}^{2}+ \sigma _{tropo,k}^{2}+ \sigma _{user,k}^{2}$ ， $\sigma _{URE,k}^{2}$ 是用于精度和连续性的星历星钟误差的标准差，可以从完好性支持信息ISM的用户测距误差（User Range Error, URE）计算得来
， $P_{fa}$ 为总误警概率（性能要求时给定的），Q为标准正态分布的尾部概率。

从北航《基于子集包含减少 AＲAIM 子集数量的方法》文献中看到，检测门限还分东北天三个不同方位的检测门限。三个方位的检测门限在计算时只需将 $P_{fa}$ 改成各自方向上被分配的误警概率即可。

这里的 $b_{nom,i}$ 为标称误差，是ISM的完好性偏差信息

对比检验统计量和检测门限，如果 $d_{k}>D_{k}$ ，则该卫星存在故障。

求解保护级PL和有效监视门限EMT

.............

SAFETY CRITICAL BOUNDS FOR PRECISE POSITIONING FOR AVIATION AND AUTONOMY 论文

2.3节

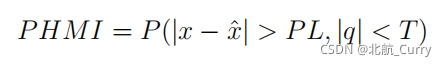
PHMI:危险误导性信息的概率或完整性风险分配
x:真实的状态
x尖号：估计状态
PL：保护级
q:检验统计量
T：一个基于误警要求和子集协方差的阈值

本质上，完整性风险是位置误差超过保护水平且测试统计数据低于阈值的概率。

ARAIM方法使用多层次解决方案分离（MHSS）将完整性风险分解为基于故障假设的组件，因此方程可以重写：

4.5节

这里提到的子集过滤器我的理解是一种新的分组策略。

FDE（故障检测排除）原始方法：

第一种方法涉及在故障检测和排除后对AIV（全视图）和子集过滤器进行简单的重新初始化。计算的唯一子集是在当前时期生成保护级别所需的子集。下图的左半部分显示了视图中所有（顶行）和其他子集（第2行之后）的测量使用示意图。

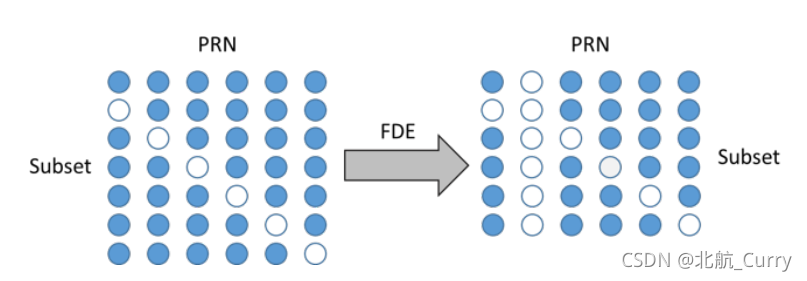
如上图右侧所示。新AIV实际上是原始集合的一个子集，但由于之前未跟踪任何新子集，因此无法使用已跟踪的AIV，必须重新初始化整个过滤器。无法使用以前跟踪的AIV的原因是，如果在给定已收敛AIV的情况下生成新子集，则这些子集将无法容忍AIV解决方案中已包含的测量上的错误。一旦过滤器重新初始化，保护级别将达到峰值，并且由于缺少PRN而导致几何结构减弱，保护级别需要比平常更长的时间才能再次收敛。

FDE（故障检测排除）新方法——one-deck filters：

为了避免在FDE后重新初始化过滤器时保护级别出现大幅跳变，开发了一种新工艺，仅在FDE情况下使用。本质上，如果我们只关注排除1颗卫星的子集，那么新FDE方法的子集将是排除两个卫星的子集，如上图图左侧所示。这些子集不包括在保护级别计算中。这样的话，检测到故障时，过滤器不需要重新初始化，因为新的AIV和子集一直都被跟踪。

新的过滤器由上图右侧的红色框突出显示。此时需要重新初始化新的one-deck上的过滤器，但只要在这些过滤器收敛（我觉得指的是保护级的收敛之前，可以看论文的4.4.1保护级收敛的图）之前未检测到其他故障，这不会影响保护级别。新的AIV是原始子集过滤器之一，新的主要子集已经在one-deck过滤器中收敛。当然，携带甲板上的过滤器在计算上是昂贵的，但是已经探索了子集分组等技术[12]，[16]，这可以显著降低计算负载。FDE后，由于几何结构减弱，保护级别略有增加，但最重要的是，它们已经收敛。