ccpc 第五届河南省省赛 I题 childhood dream

传送门

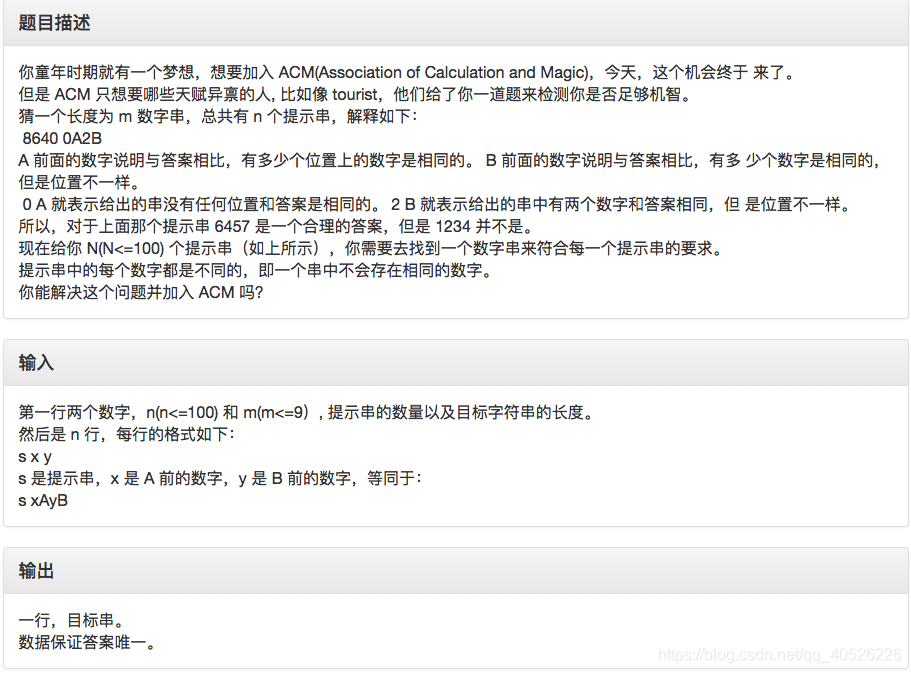
输入：
6 4
5164 3 0
5174 3 0
5194 3 0
5124 3 0
5134 3 0
5104 3 0

输出：

5184

一个巨型沙雕题！

当时榜被带歪了，直到最后几十分钟我们队才开始做，期间三个人都有了思路但都不完整。结果我们开始轮流写自己的思路，就是这样，我们三个的代码都没写完，A四题拿银牌滚粗。

题解：xjb DFS, 枝都不剪直接过?

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <iomanip>
#include <assert.h>
#include <bitset>
using namespace std;

#define eps         (1e-6)
#define LL          long long
#define pi          acos(-1.0)
#define rd(a)       (a = read())
#define ALL(a)      (a.begin(),(a.end())
#define ZERO(a)     memset(a,0,sizeof(a))
#define MINUS(a)    memset(a,0xff,sizeof(a))
#define IOS         cin.tie(0) , cout.sync_with_stdio(0)
#define PRINT(a,b)  cout << "#" << (a) << " " << (b) << endl
#define DEBUG(a,b)  cout << "$" << (a) << " " << (b) << endl
#define line        cout << "\n--------------------\n"

const LL INF = 0x3f3f3f3f;
const int mod = 1e9+7;
const int maxn = 5e6+3;

struct in{
    char s[12];
    int a,b;
}that[120];

int n,m;
bool ok(char s[]){
    for(int i=0; i<n; ++i) {
        int na, nb;
        na = nb = 0;
        for (int j = 0; j < m; ++j) {
            if(s[j] == that[i].s[j]){
                ++na;
            }
            for(int k = 0; k<m; ++k){
                if(s[j] == that[i].s[k] && j != k){
                    ++nb;
                }
            }
        }
        if(na != that[i].a || nb!= that[i].b){
            return false;
        }
    }
    return true;
}

bool f = false;
void dfs(int deep, char s[], bool vis[]){
    if(f == true)    return;
    if(deep == m){
        if(ok(s)){
            f = true;
            for(int i=0; i<m; ++i)
                printf("%c",s[i]);
        }
        return;
    }

    for(int i=0; i<=9; ++i){
        if(vis[i]) continue;

        vis[i] = true;

        char t[11];
        strcpy(t, s);
        t[deep] = i + '0';

        dfs(deep+1, t, vis);
        vis[i] = false;
    }
}

int main() {
    cin >> n >> m;
    for(int i=0; i<n; ++i){
        cin >> that[i].s >> that[i].a >> that[i].b;
    }

    bool vis[20];
    char s[11];
    ZERO(vis);
    ZERO(s);

    dfs(0,s,vis);
    return 0;
}