本篇内容零散记录一些机器学习优化方面的小知识,防止遗忘。都是一些有趣的理解,会不定期更新
机器学习中的优化算法
https://www.bilibili.com/video/BV1uZ4y1u7Ri?t=3131
https://zhuanlan.zhihu.com/p/158215009
①机器学习=建模+优化+评估
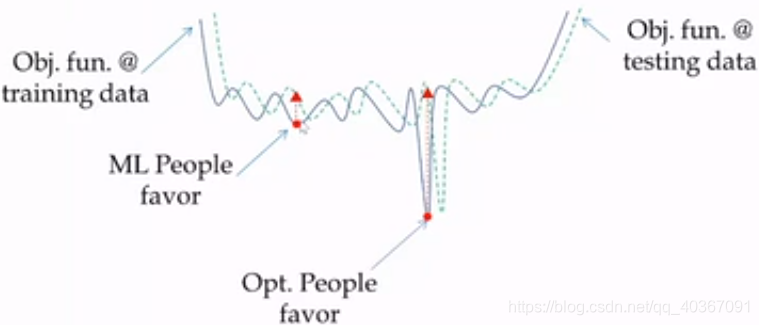
②纯优化关注全局最小点,机器学习优化关注局部最小点。因为机器学习更关注泛化误差,纯优化则关注原始误差。如下图所示,训练集和测试集独立同分布,则反映在下图中就表现为数据分布相同但略有错位,这是局部最小点的泛化能力显然更强。
③零阶、一阶、二阶优化算法:是指用到函数值、导数、二阶导数。机器学习中一般都是一阶算法,即使用到二阶算法也是用的一些近似技巧,这保证了计算量的affordable。
④机器学习问题优化技巧:临近算子(函数不光滑不可导时可以做近似梯度)、对偶问题(原问题难以求解可以转成对偶问题)和随机采样(数据量过大导致计算量太大,可以只随机采样少部分数据来优化)。
⑤机器学习优化可分为无约束优化和带约束优化:
=>无约束优化:函数光滑可导时可以使用梯度下降等一阶梯度求导方法,或者二阶梯度近似方法;函数不光滑不可导时有一些近似方法,如次梯度、函数平滑、共轭梯度、近似梯度等。
=>带约束优化:梯度投影(仍优化原来的目标函数,正常梯度下降,但算完梯度之后要投影到可行域约束范围)、罚函数(就是正则项,把约束加入目标函数一起优化)、条件梯度、黎曼优化等。
从算子角度理解优化算法
https://zhuanlan.zhihu.com/p/150605754
①优化需要多步迭代的原因:如果优化的目标函数是凸函数,那么局部最优点就等于全局最优点,那么就不需要多步迭代。然而机器学习中的问题很多时候都是非凸问题,所以不仅需要多步迭代,还需要多起点进行启发式搜索。因为是多步迭代,所以这类优化要特别关注优化算子的收敛性。
②优化算子的导出方法:优化算子其实就是一个优化方向的指引,这个优化方向一般是根据我们要寻找的最优解的必要条件推导出来。因为是必要条件,也即最优解的某个属性必须满足某个值,所以我们可以用当前属性值距离最优解的远近来指导方向。例如:我们通常所用的一阶优化条件:f’(x)=0,我们把优化变量x加入,得到:x = x - α·f’(x)。这就是我们梯度下降公式的由来,不是随机定义的,这个公式实际反映了我们是以f’(x)=0作为最终的收敛目标。显然当xk无限接近xk+1时,左右x消掉,f’(x)就等于0。





















 1240
1240

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








