flow的理论背景

数学推理20221028

来源b站shuhuai008

本质：设定可逆函数$f$和易于求解的雅可比矩阵

李宏毅的课件：Flow

生成模型

• 生成模型可以分为四个类别：自回归、GAN、VAE、flow-based（基于流）。以图像生成为例，自回归模型需要逐像素地生成整张图像，每次新生成的像素会作为生成下一个像素的输入。这种模型计算成本高，并行性很差，在大规模生成任务中性能有限。上述的 WaveNet 就是一种自回归模型，最大的缺点就是慢。其它典型的自回归模型还有 PixelRNN 和 PixelCNN。此外，自回归模型也是可逆的。相对于自回归模型，基于流的生成模型的优势是其并行性。

• 相对于 VAE 和 GAN，基于流的生成模型的优势是：可以用隐变量精确地建模真实数据的分布，即精确估计对数似然，得益于其可逆性。而 VAE 尽管是隐变量模型，但只能推断真实分布的近似值，而隐变量分布与真实分布之间的 gap 是不可度量的，这也是 VAE 的生成图像模糊的原因。GAN 是一种学习范式，并不特定于某种模型架构，并且由于其存在两个模型互相博弈的特点，理论的近似极限也是无法确定的。基于流的生成模型却可以在理论上保证可以完全逼近真实的数据分布。

• 生成模型的本质是希望能够拟合一个概率分布，深度神经网络可以拟合任何的函数，但是不能拟合任何的概率分布，因为概率分布有非负性和归一性的本质。这样，直接能写的分布只有离散分布和连续的高斯分布。

• 从严格意义讲，图像是由有限个像素组成的，每个像素的取值也是离散的，有限的，因此可以通过离散分布来描述图像的分布，pixel RNN就是基于这个思路做的，“自回归流”的思路。缺点是无法并行，计算量很大。

• 但是实际生活中，很多分布是连续的，因此研究连续的概率分布很有必要。

• 常见的概率分布函数类型：
  

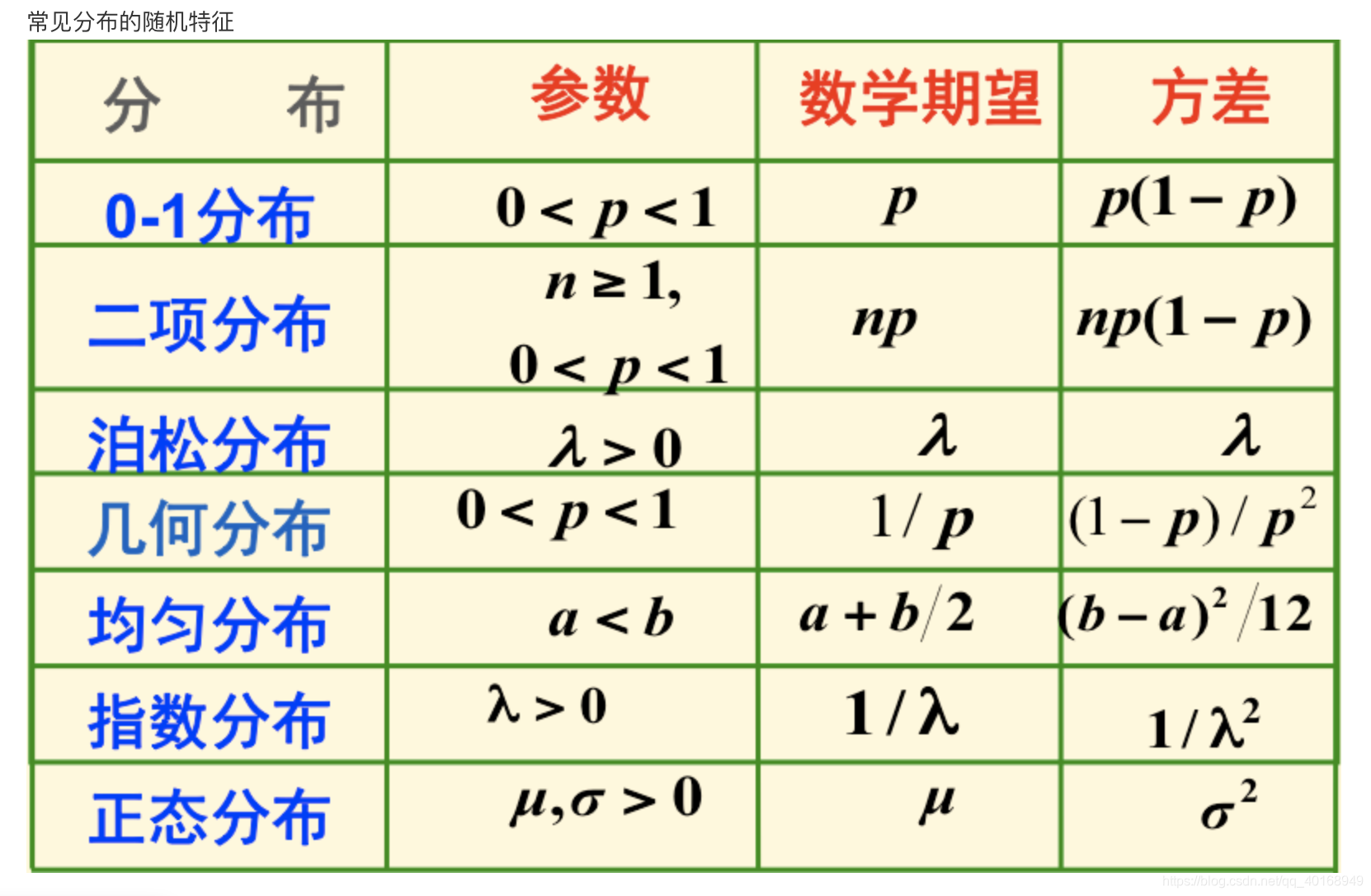
• 我们通常通过积分的形式创造更多的概率分布类型

其中$q(z)$是高斯分布，$q(x|z)$可以是任何形式的高斯分布或者狄拉克分布，原则上这个公式可以拟合任何分布。

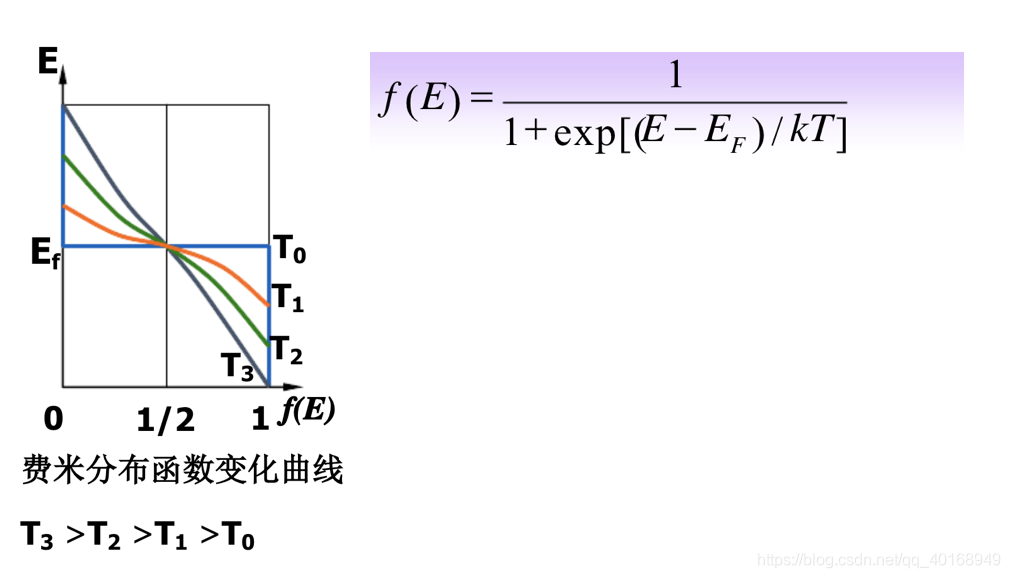
• 概率函数-----在已知一些参数的情况下，预测接下来的观测所得到的结果
• 似然函数-----在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。

flow模型

flow模型将$q(x|z)$记做狄拉克分布，选择直接计算积分。而且$g(z)$是可逆函数

$q(z)$是高斯分布，假设初始是标准正态分布，均值0，方差1，类似于batch norm，对数据进行归一化

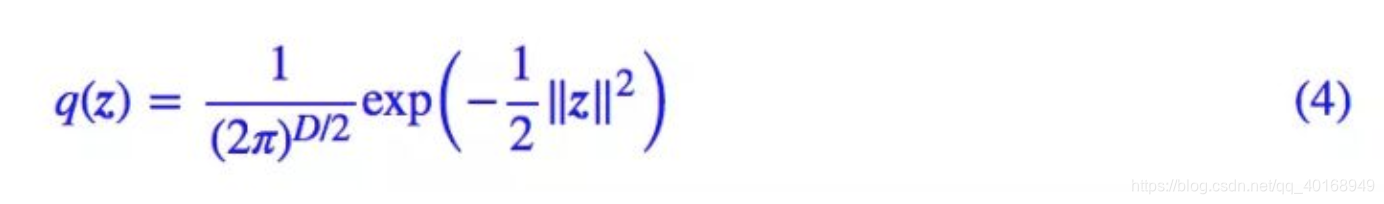
想要求$q(x)$，根据公式（1），可以写成

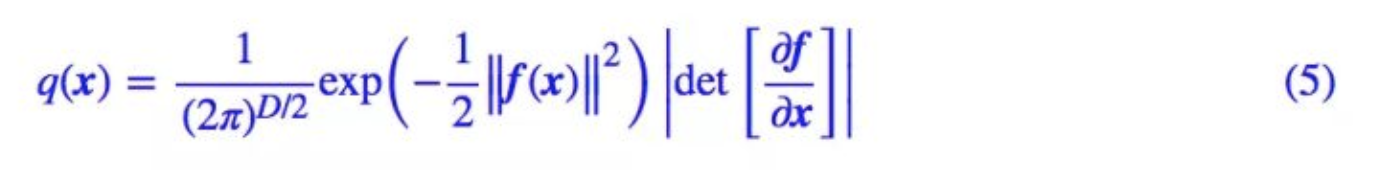
取对数之后写作

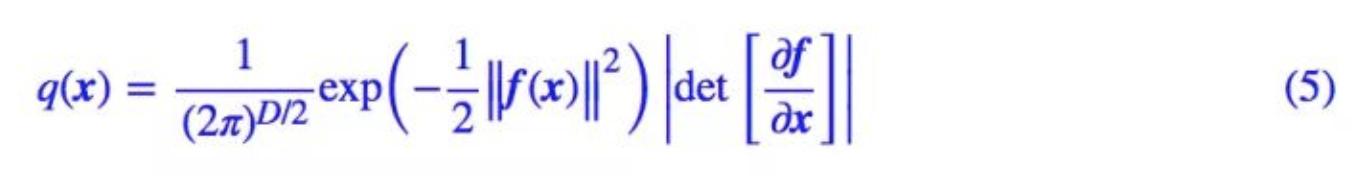
为了保证$q(x)$的求得，需要保证

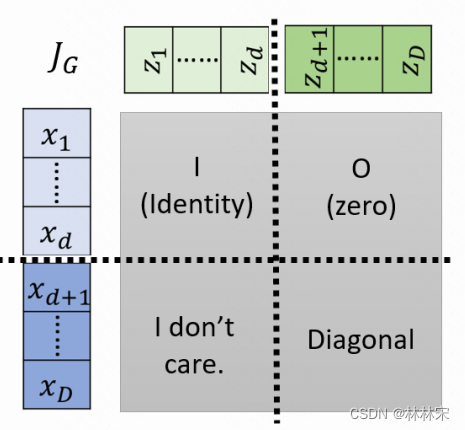
• $f(x)$可逆，对应的逆函数$g(z)$就是我们要的生成模型
• 对应的雅可比矩阵好求

变换设计

加性耦合

• 可逆性要求只能是乘加操作
• 雅可比矩阵好求：行列式是三角行列式形式
  《NICE: Non-linear Independent Components Estimation》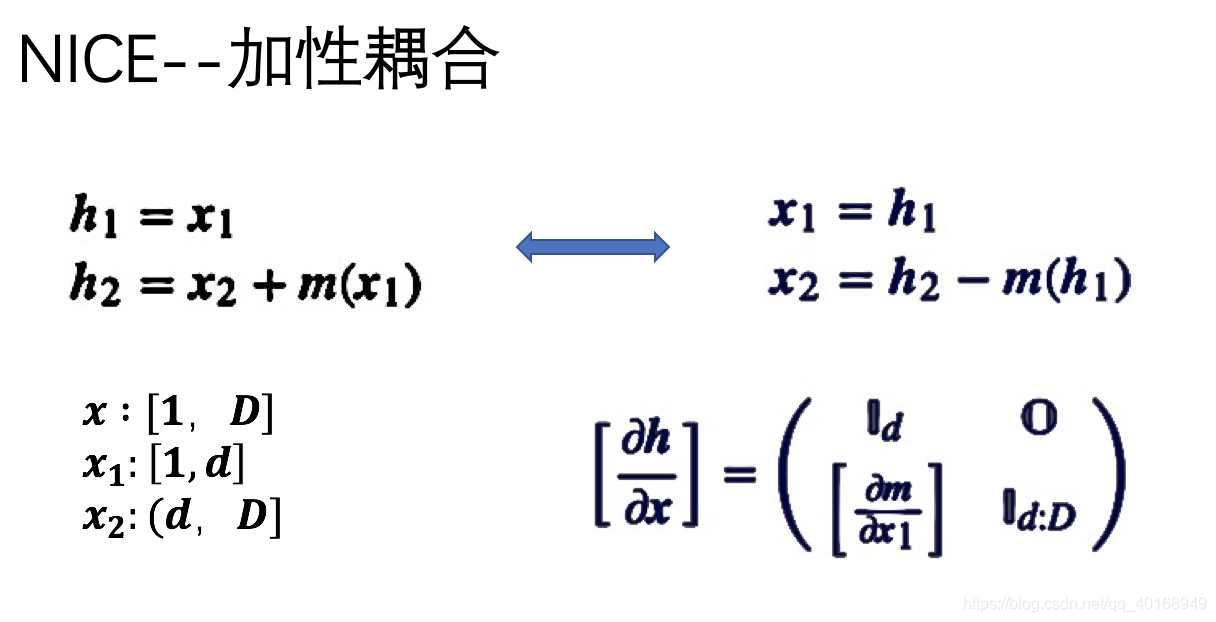
  Ref:NICE: Non-linear Independent Components Estimation
  多次乘加操作增强拟合能力
  
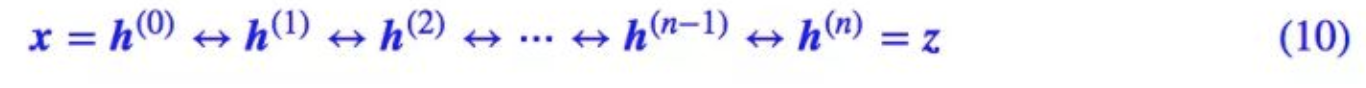
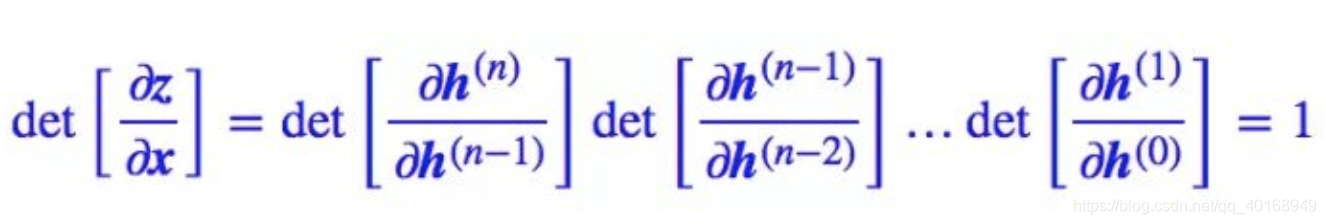
• 因为 $\frac{\partial h1}{\partial x}=1$，矩阵对角线乘积=1
  

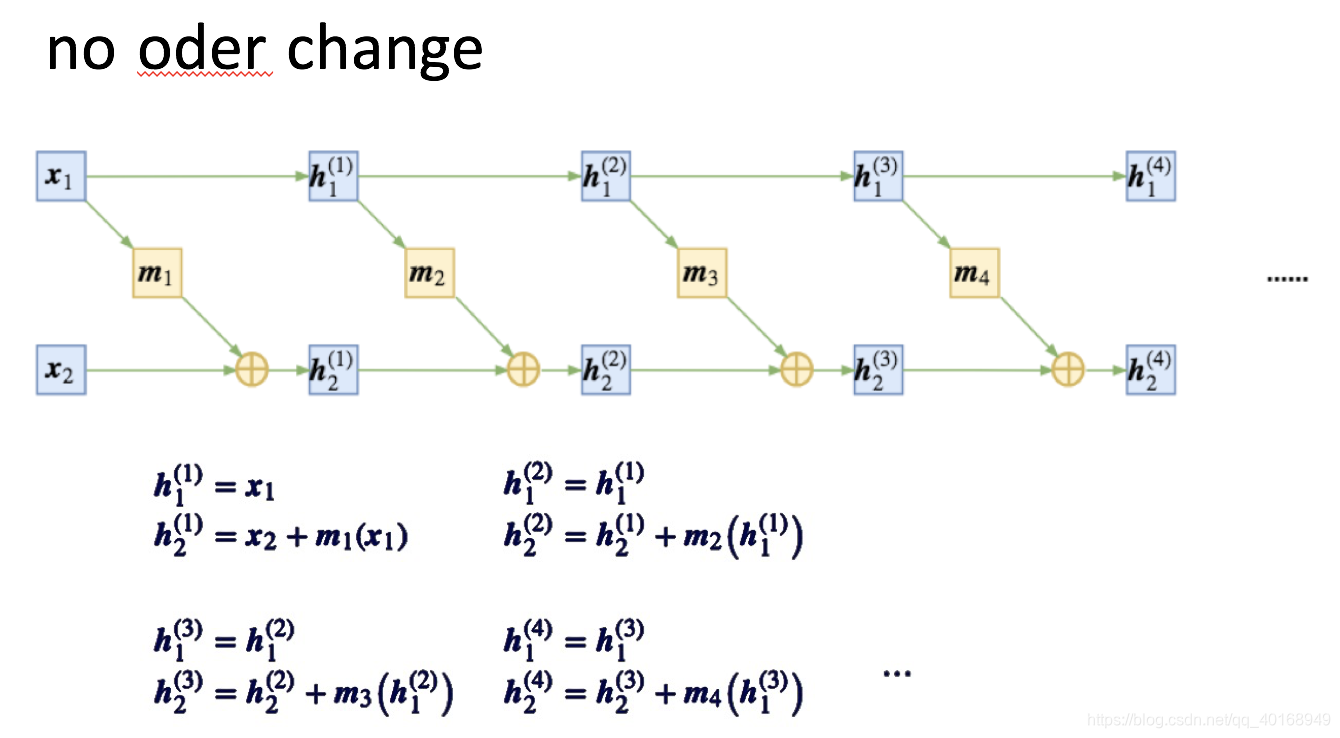
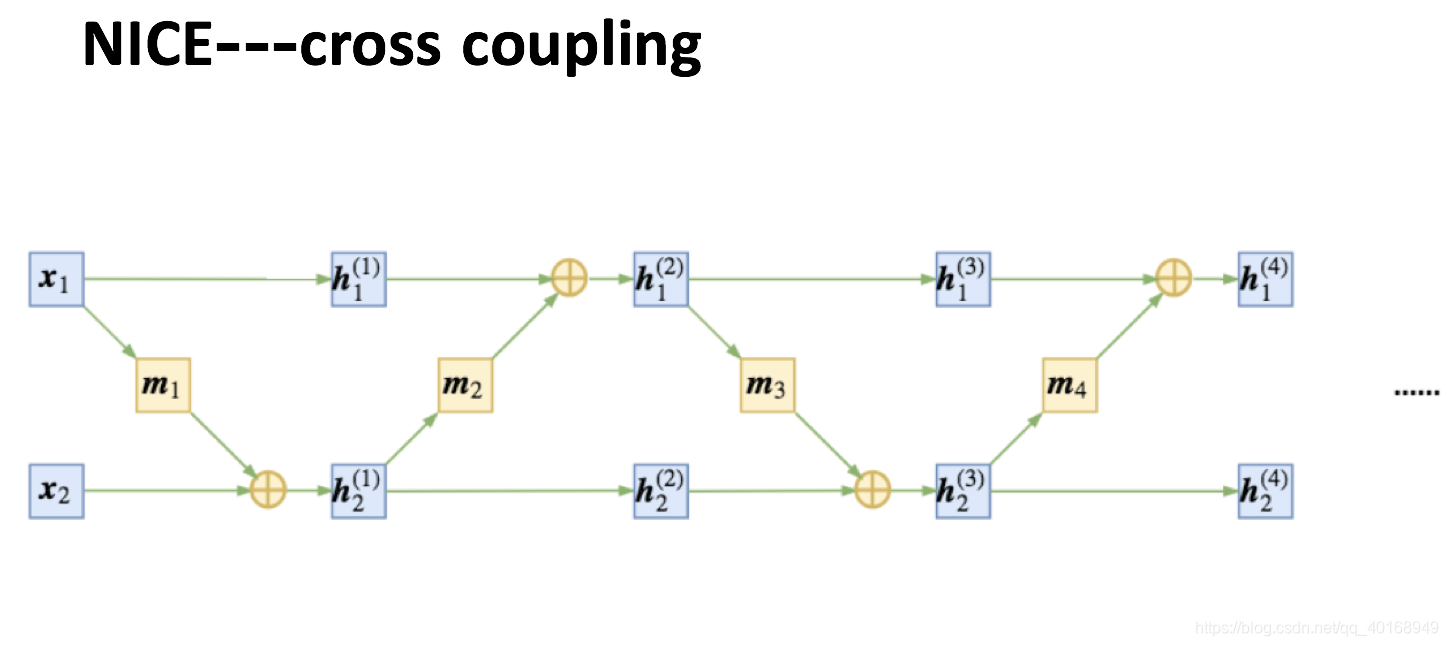
单纯的加性耦合会导致从头到尾始终有一部分数据没有参与变换，因此，在每次进行加性耦合前，打乱或反转输入的各个维度的顺序，或者简单地直接交换这两部分的位置，使得信息可以充分混合。

为了使数据充分的混合，在每次乘加操作或者仿射变换之后将数据进行随机打乱处理。

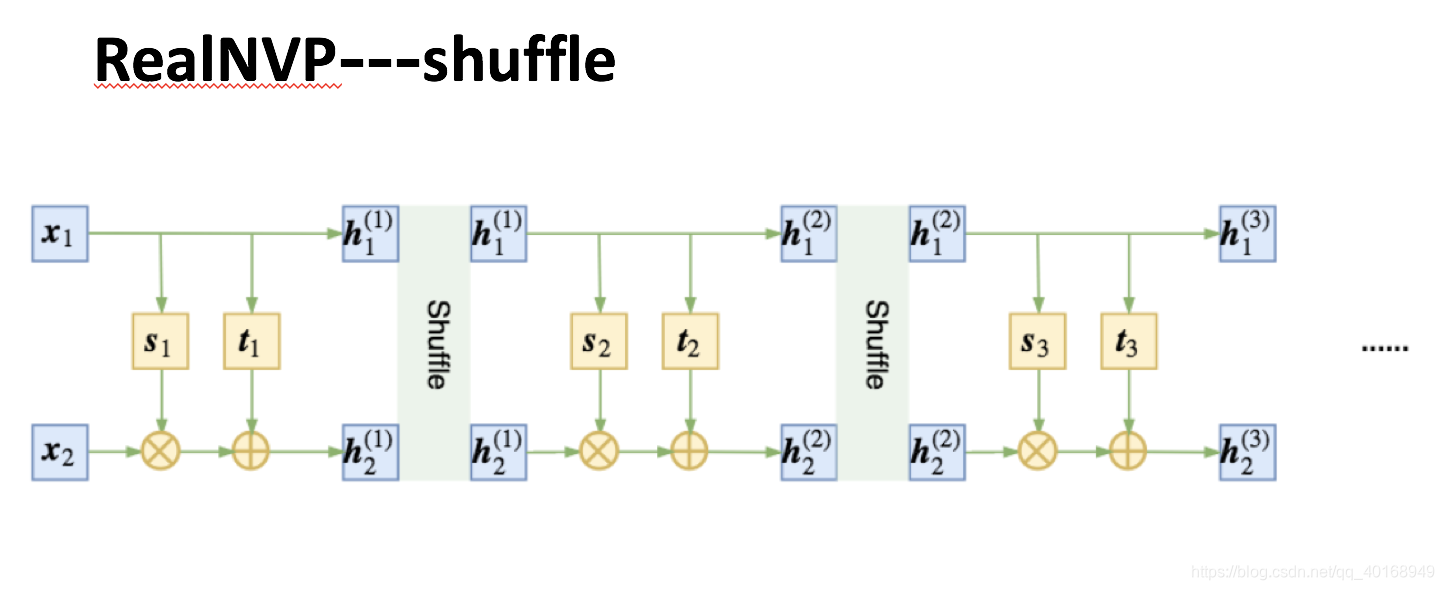
仿射耦合

flow 是基于可逆变换的，所以当模型训练完成之后，我们同时得到了一个生成模型和一个编码模型。但也正是因为可逆变换，随机变量 z 和输入样本 x 具有同一大小。

当我们指定 z 为高斯分布时，它是遍布整个 D 维空间的，D 也就是输入 x 的尺寸。但虽然 x 具有 D 维，但它未必就真正能遍布整个 D 维空间，比如 MNIST 图像虽然有 784 个像素，但有些像素不管在训练集还是测试集，都一直保持为 0，这说明它远远没有 784 维那么大。

也就是说，flow 这种基于可逆变换的模型，天生就存在比较严重的维度浪费问题：输入数据明明都不是 D 维流形，但却要编码为一个 D 维流形，这可行吗？

为了解决这个情况，NICE 引入了一个尺度变换层，它对最后编码出来的每个维度的特征都做了个尺度变换，也就是 $z=s\otimes h^{(n)}$ 这样的形式，其中 s=(s1,s2,…,sD) 也是一个要优化的参数向量（各个元素非负）。这个 s 向量能识别该维度的重要程度（越小越重要，越大说明这个维度越不重要，接近可以忽略），起到压缩流形的作用。
== real-valued non-volume preserving (real NVP) ==
Density estimation using Real NVP

由此算得它的对角矩阵也不再是1，行列式乘积是$diag(s)=\prod s_i$
于是（6）式的对数似然可以写成

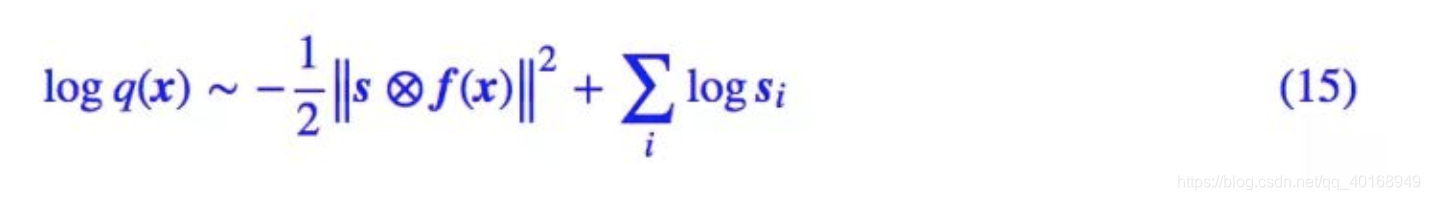
为什么这个尺度变换能识别特征的重要程度呢？其实这个尺度变换层可以换一种更加清晰的方式描述：我们开始设 z 的先验分布为标准正态分布，也就是各个方差都为 1。

事实上，我们可以将先验分布的方差也作为训练参数，这样训练完成后方差有大有小，方差越小，说明该特征的“弥散”越小，如果方差为 0，那么该特征就恒为均值 0，该维度的分布坍缩为一个点，于是这意味着流形减少了一维。
于是，（4）式写成带方差的形式

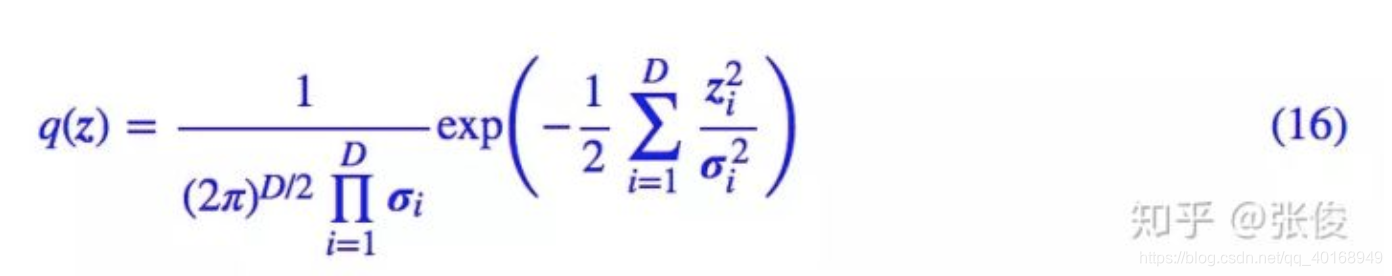
将流模型z=f(x)带入，得到

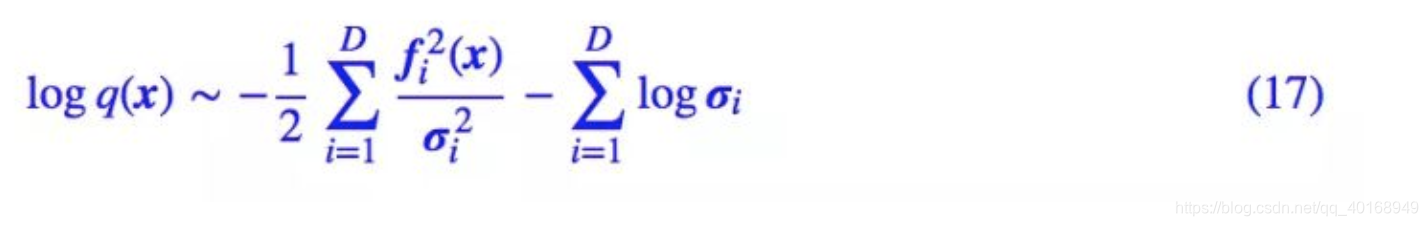
对比 (15) 式，其实就有 $s_i=1/{\sigma }_i$。所以尺度变换层等价于将先验分布的方差（标准差）也作为训练参数，如果方差足够小，我们就可以认为该维度所表示的流形坍缩为一个点，从而总体流形的维度减 1，暗含了降维的可能

squeeze

可逆的1*1卷积操作
为了保证局部相关性$h\times W\times C$压缩成$h/2\times W/2\times 4C$

参考： https://zhuanlan.zhihu.com/p/41912710

比较

相对而言，nvidia的实现版本效果会更好一些，korea小哥的有消除不掉的颤音，但是nvidia就block数目和block内部的sub-layer而言都会更多一些，因为没有跑多机训练的版本，所以没有很明确的进行对比。