comet OJ 热身赛——dijkstra

最新推荐文章于 2022-11-06 21:54:36 发布

luer9

最新推荐文章于 2022-11-06 21:54:36 发布

阅读量198

点赞数

CC 4.0 BY-SA版权

分类专栏： dijkstra算法图论

本文链接：https://blog.youkuaiyun.com/qq_40046426/article/details/89980946

图论同时被 2 个专栏收录

66 篇文章

订阅专栏

dijkstra算法

18 篇文章

订阅专栏

博主曾觉得一道题难而遗忘，如今再看发现不算难。题目涉及在直线、圆上和圆内运动不消耗体力，难点在于建图，将L1、L2和n个圆分别看作点，在它们之间建图，最后用Dijkstra算法求最短路，并给出了代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

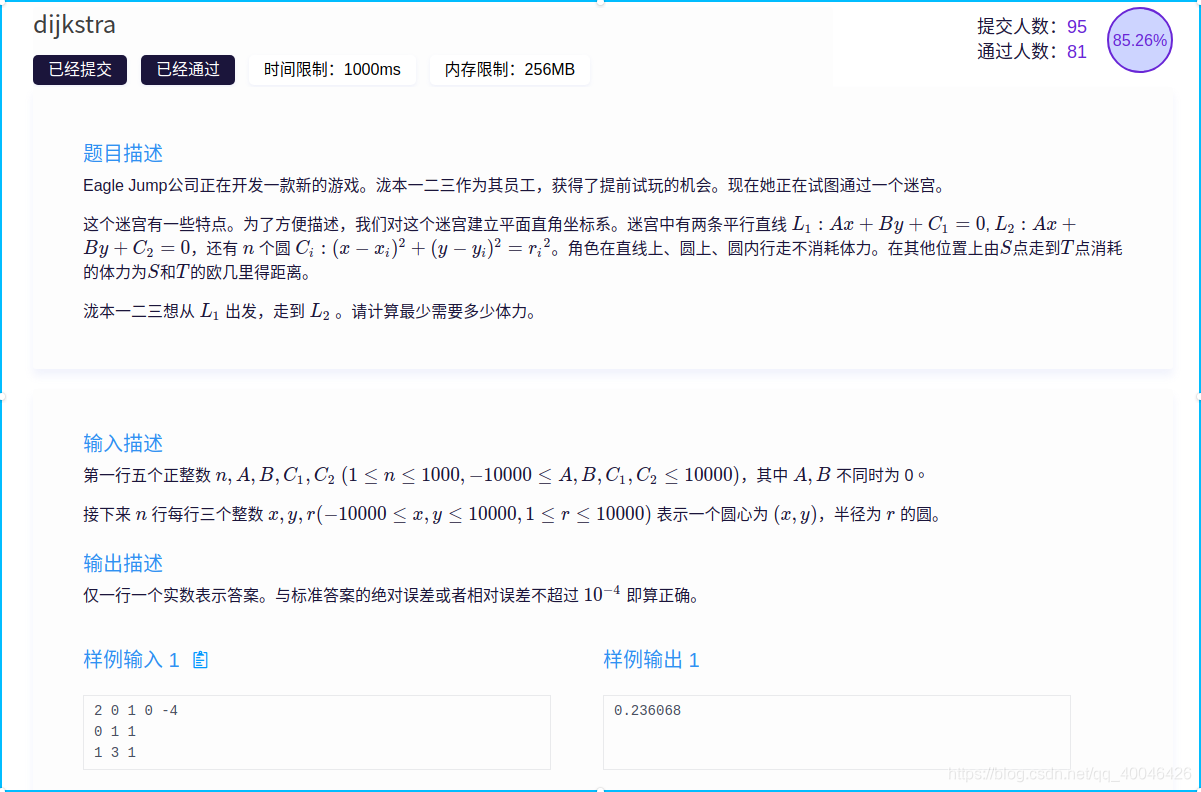
题目如上

当时没有好好看题，感觉很难，所以渐渐的遗忘了这道题，今天看这道题，也不算难，补一下吧……

下方的图可以自动忽略了，（主要是自己的思路都在这张图上，所以就放上了）

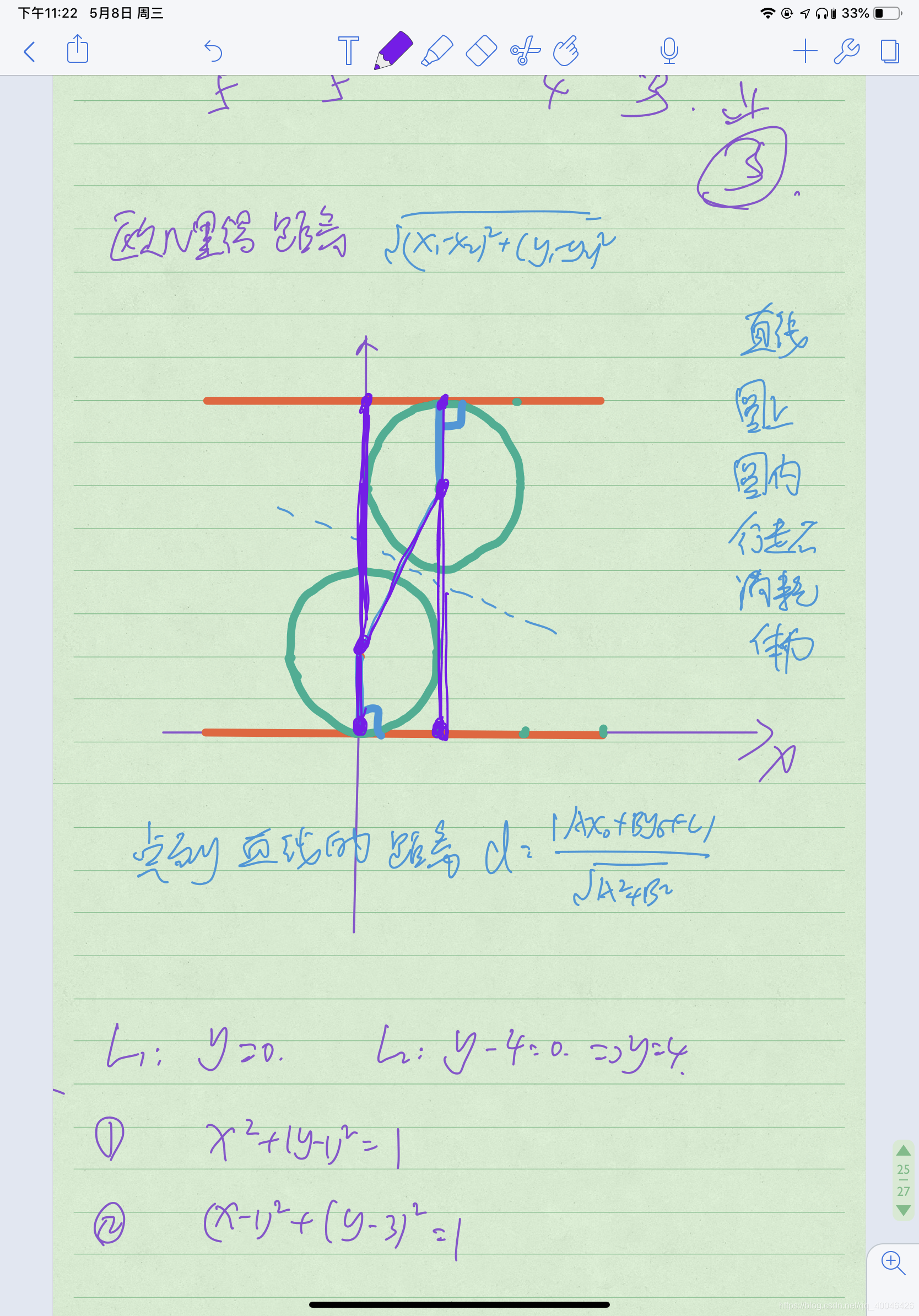
在直线，圆上，圆内运动时不消耗体力。难点主要是建图吧，想通了就很简单了……

将L1看成第0个点，L2是第n+1个点，n个圆是n个点，线和圆点(距离-r)，圆点和圆点(距离-r1-r2)之间建图，然后用dijkstra求最短路即可。

代码如下。

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define Max 1111
using namespace std;
int n, A, B, C1, C2;
int vis[Max];
double mapp[Max][Max], dis[Max];
struct Cir
{
    int x, y, r;
}cir[Max];
//欧几里得距离
double DotLen(Cir a,Cir b)
{
    return sqrt((a.x - b.x) * (a.x - b.x) * 1.0 + (a.y - b.y) * (a.y - b.y)*1.0);
}
//圆点到直线的距离
double LineLen(int a,int b,int c,Cir cc)
{
    return fabs(a * cc.x * 1.0 + b * cc.y * 1.0 + c * 1.0) / (sqrt(a * a * 1.0 + b * b * 1.0));
}
void dijkstra()
{
    for (int i = 0; i <= n+1;i++)
    {
        dis[i] = mapp[0][i];
        vis[i] = 0;
    }
    vis[0] = 1;
    dis[0] = 0;
    for (int i = 0; i <= n;i++)
    {
        double minn = inf;
        int k = -1;
        for (int j = 0; j <= n + 1;j++)
        {
            if(!vis[j]&&dis[j]<minn)
            {
                minn = dis[j];
                k = j;
            }
        }
        vis[k] = 1;
        for (int u = 0; u <= n + 1;u++)
        {
            if(!vis[u]&&dis[u]>dis[k]+mapp[k][u])
            {
                dis[u] = dis[k] + mapp[k][u];
            }
        }
    }
}
int main()
{
    ios::sync_with_stdio(0);
    cin >> n >> A >> B >> C1 >> C2;
    /*0->L1 n+1 -> L2*/
    for (int i = 0; i <= n + 1;i++){
        for (int j = 0; j <= n + 1; j++)
        {
            if(i==j)
                mapp[i][j] = 0;
            else
                mapp[i][j] = mapp[j][i] = inf;
        }
    }
    for (int i = 1; i <= n;i++)
    {
        cin >> cir[i].x >> cir[i].y >> cir[i].r;
        double len1 = LineLen(A, B, C1, cir[i]);
        //处理圆点和直线
        if((len1-cir[i].r)>=0)
            mapp[0][i] = mapp[i][0] = len1 - cir[i].r;
        else
            mapp[0][i] = mapp[i][0] = 0;
        double len2 = LineLen(A, B, C2, cir[i]);
        if((len2-cir[i].r)>=0)
            mapp[n + 1][i] = mapp[i][n + 1] = len2 - cir[i].r;
        else
            mapp[n + 1][i] = mapp[i][n + 1] = 0;
    }
    //处理圆点与圆点
    for (int i = 1; i <= n;i++)
    {
        for (int j = i+1; j <= n;j++)
        {
            double len = DotLen(cir[i], cir[j]);
            if((len-cir[i].r-cir[j].r)>=0)
                mapp[i][j] = mapp[j][i] = len - cir[i].r - cir[j].r;
            else
                mapp[i][j] = mapp[j][i] = 0;
        }
    }
    dijkstra();
    cout << fixed << setprecision(6) << dis[n + 1] << endl;
    return 0;
}