斐波那契数列(Fibonacci sequence),又称 黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“ 兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以 递归的方法定义:F(0)=0,F(1)=1, F(n)=F(n-1)+F(n-2)(n>=2,n∈N*)
递推公式
斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
如果设F(n)为该数列的第n项(n∈N*),那么这句话可以写成如下形式::F(n)=F(n-1)+F(n-2)
显然这是一个线性 递推数列。
通项公式
因为存在无理数 ,所以这个公式不是特别精确。
https://blog.youkuaiyun.com/qq_40046426/article/details/81484007这个题就运用了上面的公式
(如上,又称为“比内公式”,是用 无理数表示有理数的一个范例。)
注:此时
递归模板。
int fib(int n)
{
if(n==1||n==2) return 1;
return fib(n-1)+fib(n-2);
}利用矩阵乘法 来 求 斐波那契。

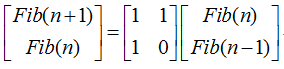
不停地利用这个式子迭代右边的列向量,会得到下面的式子:

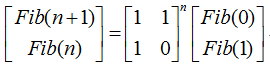
这样,问题就转化为如何计算这个矩阵的n次方了,可以采用快速幂的方法。快速幂_百度百科是利用结合律快速计算幂次的方法。比如我要计算 ,我们知道
,我们知道 ,而
,而 可以通过
可以通过 来计算,
来计算, 而可以通过
而可以通过 计算,以此类推。通过这种方法,可以在O(lbn)的时间里计算出一个数的n次幂。
计算,以此类推。通过这种方法,可以在O(lbn)的时间里计算出一个数的n次幂。
矩阵乘法模板。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
#include <queue>
#include <stack>
using namespace std;
const int MOD = 10000;
struct matrix//定义矩阵结构体
{
int m[2][2];
}ans, base;
matrix multi(matrix a, matrix b)//定义矩阵乘法
{
matrix tmp;
for(int i = 0; i < 2; ++i)
{
for(int j = 0; j < 2; ++j)
{
tmp.m[i][j] = 0;
for(int k = 0; k < 2; ++k)
tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] * b.m[k][j]) % MOD;
}
}
return tmp;
}
int fast_mod(int n) // 求矩阵 base 的 n 次幂
{
base.m[0][0] = base.m[0][1] = base.m[1][0] = 1;
base.m[1][1] = 0;
ans.m[0][0] = ans.m[1][1] = 1; // ans 初始化为单位矩阵
ans.m[0][1] = ans.m[1][0] = 0;
while(n)
{
if(n & 1) //实现 ans *= t; 其中要先把 ans赋值给 tmp,然后用 ans = tmp * t
ans = multi(ans, base);
base = multi(base, base);
n >>= 1;
}
return ans.m[0][1];
}
int main()
{
int n;
while(scanf("%d", &n) && n != -1)
{
printf("%d\n", fast_mod(n));
}
return 0;
}
/*
0 0
9 34
99999999 626
1000000000 6875
-1
*/










 本文详细介绍了斐波那契数列的概念及其数学定义,包括递推公式和通项公式的推导,并提供了使用递归及矩阵快速幂法求解斐波那契数的具体实现代码。
本文详细介绍了斐波那契数列的概念及其数学定义,包括递推公式和通项公式的推导,并提供了使用递归及矩阵快速幂法求解斐波那契数的具体实现代码。
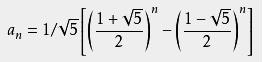
















 1547
1547

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








