CODING

（壹）树

二叉树前中后序遍历统一模板

前序（根左右）

LC144. 二叉树的前序遍历

题目链接

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        ans = []  # 用于存储前序遍历结果的列表
        if not root:  # 如果根节点为空，直接返回空列表
            return ans
        stack = []  # 初始化一个栈，用于辅助遍历
        stack.append(root)  # 将根节点入栈
        while stack:  # 当栈不为空时，继续循环
            p = stack[-1]  # p指向栈顶元素，但不弹出
            if p:  # 如果栈顶元素不为空（即不是None）
                p = stack.pop()  # 将栈顶元素弹出并重新赋值给p
                # 将右子节点入栈（注意：此时不入处理，只是暂存）
                if p.right:
                    stack.append(p.right)
                # 将左子节点入栈（注意：此时也不处理，只是暂存）
                if p.left:
                    stack.append(p.left)
                # 将当前节点重新入栈，用于后续处理其值
                stack.append(p)
                # 插入一个None作为标记，表示下一次循环时需要处理该节点的值
                stack.append(None)
            else:  # 如果栈顶元素为空（即之前的None），表示需要处理其前一个节点的值
                stack.pop()  # 弹出这个None标记
                p = stack.pop()  # 弹出需要处理的节点
                ans.append(p.val)  # 将节点的值添加到结果列表中
        return ans  # 返回前序遍历的结果列表

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var preorderTraversal = function (root) {
    let res = []
    if (root===null) {
        return res
    }
    let st = []
    st.push(root)
    while (st.length > 0) {
        let p = st[st.length - 1]
        if (p !== null) {
            p = st.pop()
            if (p.right) {
                st.push(p.right)
            }
            if (p.left) {
                st.push(p.left)
            }
            st.push(p)
            st.push(null)
        } else {
            st.pop()
            p = st.pop()
            res.push(p.val)
        }
    }
    return res
};

---

中序（左根右）

LC94. 二叉树的中序遍历

题目链接

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        ans = []
        if not root:
            return ans
        stack = []
        stack.append(root)
        while stack:
            p = stack[-1]
            if p:
                p = stack.pop()
                # 右
                if p.right:
                    stack.append(p.right)
                # 根
                stack.append(p)
                stack.append(None)
                # 左
                if p.left:
                    stack.append(p.left)
            else:
                stack.pop()
                p = stack.pop()
                ans.append(p.val)
        return ans

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function (root) {
    let res = []
    if (root === null) {
        return res
    }
    let st = []
    st.push(root)
    while (st.length > 0) {
        let p = st[st.length - 1]
        if (p !== null) {
            p = st.pop()
            if (p.right) {
                st.push(p.right)
            }
            st.push(p)
            st.push(null)
            if (p.left) {
                st.push(p.left)
            }
        } else {
            st.pop()
            p = st.pop()
            res.push(p.val)
        }
    }
    return res
};

---

后序（左右根）

LC145. 二叉树的后序遍历

题目链接

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        ans = []
        if not root:
            return ans
        stack = []
        stack.append(root)
        while stack:
            p = stack[-1]
            if p:
                # 根
                stack.append(None)
                # 右
                if p.right:
                    stack.append(p.right)
                # 左
                if p.left:
                    stack.append(p.left)
            else:
                stack.pop()
                p = stack.pop()
                ans.append(p.val)
        return ans

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var postorderTraversal = function (root) {
    let res = []
    if (root === null) {
        return res
    }
    let st = []
    st.push(root)
    while (st.length > 0) {
        let p = st[st.length - 1]
        if (p !== null) {
            st.push(null)
            if (p.right) {
                st.push(p.right)
            }
            if (p.left) {
                st.push(p.left)
            }
        } else {
            st.pop()
            p = st.pop()
            res.push(p.val)
        }
    }
    return res
};

文章链接

LC108. 将有序数组转换为平衡二叉搜索树

文章链接
108. 将有序数组转换为二叉搜索树

题目要求

(一)分治法（递归）

要将一个升序排列的整数数组转换为一棵平衡的二叉搜索树（BST），我们可以采用 分治法。具体思路是：

1. 找到数组的中间元素，将其作为树的根节点。
2. 递归处理左半部分数组，构建左子树。
3. 递归处理右半部分数组，构建右子树。

这种方法可以确保生成的二叉搜索树是平衡的，因为每次递归都选择中间元素作为根节点，左右子树的节点数相差不超过 1。

以下是 JavaScript 的实现代码：

代码实现

function TreeNode(val, left, right) {
    this.val = (val === undefined ? 0 : val);
    this.left = (left === undefined ? null : left);
    this.right = (right === undefined ? null : right);
}

function sortedArrayToBST(nums) {
    // 递归函数：构建平衡二叉搜索树
    const buildTree = (left, right) => {
        if (left > right) {
            return null; // 递归终止条件
        }

        // 找到中间元素作为根节点
        const mid = Math.floor((left + right) / 2);
        const root = new TreeNode(nums[mid]);

        // 递归构建左子树和右子树
        root.left = buildTree(left, mid - 1);
        root.right = buildTree(mid + 1, right);

        return root;
    };

    return buildTree(0, nums.length - 1);
}

// 示例用法
const nums = [-10, -3, 0, 5, 9];
const bst = sortedArrayToBST(nums);

// 打印树的结构（中序遍历）
function inorderTraversal(root) {
    if (!root) return [];
    return [...inorderTraversal(root.left), root.val, ...inorderTraversal(root.right)];
}

console.log(inorderTraversal(bst)); // 输出: [-10, -3, 0, 5, 9]

---

代码解释

1. TreeNode 构造函数：

   • 定义了二叉树的节点结构，包含 val、left 和 right。

2. sortedArrayToBST 函数：

   • 主函数，接受一个升序数组 nums，返回平衡二叉搜索树的根节点。

3. buildTree 递归函数：

   • 参数 left 和 right 表示当前子数组的左右边界。
   • 如果 left > right，说明当前子数组为空，返回 null。
   • 找到中间元素 nums[mid]，将其作为当前子树的根节点。
   • 递归构建左子树（left 到 mid - 1）和右子树（mid + 1 到 right）。

4. 中序遍历验证：

   • 使用 inorderTraversal 函数对生成的二叉搜索树进行中序遍历，确保结果与输入数组一致。

---

示例

输入

const nums = [-10, -3, 0, 5, 9];

生成的平衡二叉搜索树结构

      0
     / \
   -3   9
   /   /
-10  5

中序遍历结果

[-10, -3, 0, 5, 9]

---

复杂度分析

1. 时间复杂度：

   • 每次递归都将数组分成两半，时间复杂度为 O(n)，其中 n 是数组的长度。

2. 空间复杂度：

   • 递归调用栈的深度为 O(log n)，因为树是平衡的。

---

总结

通过分治法，我们可以高效地将一个升序数组转换为平衡的二叉搜索树。这种方法的时间复杂度和空间复杂度都非常优秀，适合处理大规模数据。

---

(二)栈（非递归）

非递归方法也可以通过 迭代 和 栈 来实现将升序数组转换为平衡二叉搜索树。虽然递归方法更直观，但非递归方法可以避免递归调用栈的开销，适合处理深度较大的树。

以下是使用 栈 的非递归实现方法：

代码实现

function TreeNode(val, left, right) {
    this.val = (val === undefined ? 0 : val);
    this.left = (left === undefined ? null : left);
    this.right = (right === undefined ? null : right);
}

function sortedArrayToBST(nums) {
    if (nums.length === 0) return null;

    // 栈用于存储待处理的子数组范围及其父节点
    const stack = [];
    const root = new TreeNode(); // 创建一个虚拟根节点
    stack.push({ left: 0, right: nums.length - 1, parent: root, isLeft: true });

    while (stack.length > 0) {
        const { left, right, parent, isLeft } = stack.pop();

        if (left > right) {
            // 如果当前子数组为空，跳过
            continue;
        }

        // 找到中间元素
        const mid = Math.floor((left + right) / 2);
        const node = new TreeNode(nums[mid]);

        // 将当前节点挂到父节点上
        if (isLeft) {
            parent.left = node;
        } else {
            parent.right = node;
        }

        // 将右半部分子数组和当前节点入栈
        stack.push({ left: mid + 1, right: right, parent: node, isLeft: false });
        // 将左半部分子数组和当前节点入栈
        stack.push({ left: left, right: mid - 1, parent: node, isLeft: true });
    }

    return root.left; // 返回真正的根节点
}

// 示例用法
const nums = [-10, -3, 0, 5, 9];
const bst = sortedArrayToBST(nums);

// 打印树的结构（中序遍历）
function inorderTraversal(root) {
    if (!root) return [];
    return [...inorderTraversal(root.left), root.val, ...inorderTraversal(root.right)];
}

console.log(inorderTraversal(bst)); // 输出: [-10, -3, 0, 5, 9]

---

代码解释

1. 栈的作用：

   • 栈用于存储待处理的子数组范围及其父节点信息。
   • 每个栈元素包含：
     • left 和 right：当前子数组的左右边界。
     • parent：当前子数组的父节点。
     • isLeft：当前子数组是父节点的左子树还是右子树。

2. 初始化：

   • 创建一个虚拟根节点 root，并将其与整个数组范围 [0, nums.length - 1] 入栈。

3. 迭代过程：

   • 从栈中弹出一个子数组范围及其父节点信息。
   • 如果 left > right，说明当前子数组为空，跳过。
   • 找到中间元素 nums[mid]，创建一个新节点。
   • 将新节点挂到父节点的左子树或右子树上（根据 isLeft 的值）。
   • 将右半部分子数组和当前节点入栈。
   • 将左半部分子数组和当前节点入栈。

4. 返回结果：

   • 最终返回虚拟根节点的左子树（即真正的根节点）。

---

示例

输入

const nums = [-10, -3, 0, 5, 9];

生成的平衡二叉搜索树结构

      0
     / \
   -3   9
   /   /
-10  5

中序遍历结果

[-10, -3, 0, 5, 9]

---

复杂度分析

1. 时间复杂度：

   • 每个节点只会被处理一次，时间复杂度为 O(n)，其中 n 是数组的长度。

2. 空间复杂度：

   • 栈的最大深度为 O(log n)，因为树是平衡的。

---

总结

非递归方法通过栈模拟递归过程，避免了递归调用栈的开销，适合处理大规模数据或深度较大的树。虽然代码稍复杂，但性能更优。

LC109. 有序链表转换平衡二叉搜索树

文章链接

LC109. 有序链表转换平衡二叉搜索树

题目要求

(一)快慢指针

要将一个按升序排列的单链表转换为平衡的二叉搜索树（BST），可以采用以下步骤：

1. 理解问题

• 单链表：链表中的节点按升序排列。
• 平衡二叉搜索树：树的左右子树高度差不超过1，且左子树的值小于根节点，右子树的值大于根节点。

2. 解决思路

由于链表是升序排列的，我们可以将其视为二叉搜索树的中序遍历结果。为了构建平衡的BST，我们需要找到链表的中间节点作为根节点，然后递归地构建左子树和右子树。

3. 具体步骤

1. 找到链表的中间节点：

   • 使用快慢指针法找到链表的中间节点。快指针每次走两步，慢指针每次走一步，当快指针到达链表末尾时，慢指针指向的就是中间节点。

2. 递归构建BST：

   • 将中间节点作为根节点。
   • 递归地构建左子树（链表的前半部分）和右子树（链表的后半部分）。

3. 处理边界条件：

   • 如果链表为空，返回 null。
   • 如果链表只有一个节点，直接返回该节点作为树的根节点。

4. 代码实现

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def sortedListToBST(head):
    if not head:
        return None
    
    # 找到链表的中间节点
    def findMiddle(head):
        slow = head
        fast = head
        prev = None
        
        while fast and fast.next:
            prev = slow
            slow = slow.next
            fast = fast.next.next
        
        # 断开链表
        if prev:
            prev.next = None
        
        return slow
    
    # 递归构建BST
    def buildBST(head):
        if not head:
            return None
        
        mid = findMiddle(head)
        root = TreeNode(mid.val)
        
        # 如果只有一个节点，直接返回
        if head == mid:
            return root
        
        # 递归构建左子树和右子树
        root.left = buildBST(head)
        root.right = buildBST(mid.next)
        
        return root
    
    return buildBST(head)

5. 复杂度分析

• 时间复杂度：O(N log N)，其中 N 是链表的长度。每次递归都需要找到中间节点，时间复杂度为 O(N)，递归深度为 O(log N)。
• 空间复杂度：O(log N)，递归栈的深度为 O(log N)。

6. 示例解释

对于输入 head = [-10,-3,0,5,9]：

• 中间节点是 0，作为根节点。
• 左子树由 [-10, -3] 构建，右子树由 [5, 9] 构建。
• 最终得到的平衡BST为 [0,-3,9,-10,null,5]。

7. 总结

通过找到链表的中间节点并将其作为根节点，然后递归地构建左子树和右子树，我们可以将一个升序链表转换为一个平衡的二叉搜索树。这种方法既保证了树的平衡性，又充分利用了链表的升序特性。

（贰）回溯

二叉树最长路径

文章链接

（一）递归+回溯

要找到一棵二叉树中从根节点到叶子的最长路径，并打印出这条路径，可以使用 深度优先搜索（DFS） 的方法。具体步骤如下：

1. 遍历二叉树：从根节点开始，递归遍历每个节点，记录当前路径的长度和路径上的节点。
2. 更新最长路径：当遍历到叶子节点时，比较当前路径的长度是否比已知的最长路径更长。如果是，则更新最长路径。
3. 打印路径：在遍历结束后，打印最长路径上的节点。

以下是实现代码（使用 JavaScript）：

---

代码实现

function TreeNode(val, left, right) {
    this.val = (val === undefined ? 0 : val);
    this.left = (left === undefined ? null : left);
    this.right = (right === undefined ? null : right);
}

function findLongestPath(root) {
    if (!root) return { length: 0, path: [] }; // 如果树为空，返回空路径

    let longestPath = { length: 0, path: [] }; // 存储最长路径

    // DFS 递归函数
    const dfs = (node, currentPath) => {
        if (!node) return;

        // 将当前节点加入路径
        currentPath.push(node.val);

        // 如果是叶子节点，检查当前路径是否是最长路径
        if (!node.left && !node.right) {
            if (currentPath.length > longestPath.length) {
                longestPath.length = currentPath.length;
                longestPath.path = [...currentPath]; // 更新最长路径
            }
        }

        // 递归遍历左子树和右子树
        dfs(node.left, currentPath);
        dfs(node.right, currentPath);

        // 回溯：移除当前节点
        currentPath.pop();
    };

    // 从根节点开始 DFS
    dfs(root, []);

    return longestPath;
}

// 示例用法
const root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.right = new TreeNode(6);
root.left.left.left = new TreeNode(7);

const result = findLongestPath(root);
console.log("最长路径长度:", result.length); // 输出: 4
console.log("最长路径:", result.path.join(" -> ")); // 输出: 1 -> 2 -> 4 -> 7

---

代码解释

1. TreeNode 构造函数：

   • 定义了二叉树的节点结构。

2. findLongestPath 函数：

   • 接受二叉树的根节点，返回最长路径的长度和路径。
   • 使用 longestPath 对象存储最长路径的长度和路径。

3. dfs 递归函数：

   • 参数 node 是当前节点，currentPath 是当前路径。
   • 将当前节点的值加入 currentPath。
   • 如果当前节点是叶子节点（没有左右子节点），检查当前路径是否比已知的最长路径更长。如果是，则更新 longestPath。
   • 递归遍历左子树和右子树。
   • 回溯时，移除当前节点（currentPath.pop()），以便尝试其他路径。

4. 返回结果：

   • 返回 longestPath，包含最长路径的长度和路径。

---

示例

输入二叉树结构

        1
       / \
      2   3
     / \   \
    4   5   6
   /
  7

输出

最长路径长度: 4
最长路径: 1 -> 2 -> 4 -> 7

---

复杂度分析

1. 时间复杂度：

   • 每个节点只会被访问一次，时间复杂度为 O(n)，其中 n 是二叉树的节点数。

2. 空间复杂度：

   • 递归调用栈的深度为树的高度，最坏情况下为 O(n)（树退化为链表）。
   • 存储路径的空间复杂度为 O(h)，其中 h 是树的高度。

---

总结

通过深度优先搜索（DFS）和回溯，我们可以高效地找到二叉树中从根节点到叶子的最长路径，并打印出这条路径。这种方法适用于任意二叉树，且代码清晰易懂。

（二）迭代+栈

要使用 非递归方法 找到二叉树中从根节点到叶子的最长路径，并打印出这条路径，可以通过 深度优先搜索（DFS） 的迭代实现，结合 栈 来模拟递归过程。以下是实现代码：

---

非递归实现代码

function TreeNode(val, left, right) {
    this.val = (val === undefined ? 0 : val);
    this.left = (left === undefined ? null : left);
    this.right = (right === undefined ? null : right);
}

function findLongestPath(root) {
    if (!root) return { length: 0, path: [] }; // 如果树为空，返回空路径

    let longestPath = { length: 0, path: [] }; // 存储最长路径
    const stack = []; // 栈用于存储节点和当前路径

    // 初始状态：根节点和空路径
    stack.push({ node: root, path: [root.val] });

    while (stack.length > 0) {
        const { node, path } = stack.pop(); // 弹出栈顶元素

        // 如果是叶子节点，检查当前路径是否是最长路径
        if (!node.left && !node.right) {
            if (path.length > longestPath.length) {
                longestPath.length = path.length;
                longestPath.path = [...path]; // 更新最长路径
            }
        }

        // 将右子节点和当前路径入栈
        if (node.right) {
            stack.push({ node: node.right, path: [...path, node.right.val] });
        }

        // 将左子节点和当前路径入栈
        if (node.left) {
            stack.push({ node: node.left, path: [...path, node.left.val] });
        }
    }

    return longestPath;
}

// 示例用法
const root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.right = new TreeNode(6);
root.left.left.left = new TreeNode(7);

const result = findLongestPath(root);
console.log("最长路径长度:", result.length); // 输出: 4
console.log("最长路径:", result.path.join(" -> ")); // 输出: 1 -> 2 -> 4 -> 7

---

代码解释

1. TreeNode 构造函数：

   • 定义了二叉树的节点结构。

2. findLongestPath 函数：

   • 接受二叉树的根节点，返回最长路径的长度和路径。
   • 使用 longestPath 对象存储最长路径的长度和路径。

3. 栈的使用：

   • 栈中存储的对象包含：
     • node：当前节点。
     • path：从根节点到当前节点的路径。
   • 初始状态：将根节点和路径 [root.val] 入栈。

4. 迭代过程：

   • 弹出栈顶元素，检查当前节点是否是叶子节点。
   • 如果是叶子节点，检查当前路径是否比已知的最长路径更长。如果是，则更新 longestPath。
   • 将右子节点和当前路径入栈。
   • 将左子节点和当前路径入栈。

5. 返回结果：

   • 返回 longestPath，包含最长路径的长度和路径。

---

示例

输入二叉树结构

        1
       / \
      2   3
     / \   \
    4   5   6
   /
  7

输出

最长路径长度: 4
最长路径: 1 -> 2 -> 4 -> 7

---

复杂度分析

1. 时间复杂度：

   • 每个节点只会被访问一次，时间复杂度为 O(n)，其中 n 是二叉树的节点数。

2. 空间复杂度：

   • 栈的最大深度为树的高度，最坏情况下为 O(n)（树退化为链表）。
   • 存储路径的空间复杂度为 O(h)，其中 h 是树的高度。

---

总结

通过栈模拟递归过程，我们可以用非递归方法找到二叉树中从根节点到叶子的最长路径，并打印出这条路径。这种方法避免了递归调用栈的开销，适合处理深度较大的树。

---

LC77. 组合

文章链接

LC77. 组合

题目要求

(一)回溯

要解决这个问题，我们需要生成从 [1, n] 范围内选择 k 个数的所有可能组合。组合的顺序不重要，即 [1, 2] 和 [2, 1] 被视为同一个组合。

1. 解决思路

我们可以使用回溯法（Backtracking）来生成所有可能的组合。回溯法是一种通过递归遍历所有可能解的方法，适用于组合、排列等问题。

2. 具体步骤

1. 递归函数设计：

   • 定义一个递归函数 backtrack(start, path)，其中：
     • start 表示当前可以选择的起始数字。
     • path 是当前已经选择的数字组合。
   • 如果 path 的长度等于 k，说明已经找到一个有效的组合，将其加入结果集。
   • 否则，从 start 开始遍历到 n，依次选择数字并递归调用。

2. 剪枝优化：

   • 在递归过程中，如果剩余的数字不足以填满 k 个数的组合，可以直接剪枝，避免无效递归。

3. 初始化调用：

   • 从 1 开始调用递归函数，初始 path 为空。

3. 代码实现

def combine(n, k):
    def backtrack(start, path):
        # 如果当前路径长度等于 k，加入结果集
        if len(path) == k:
            result.append(path.copy())
            return
        
        # 遍历可能的数字
        for i in range(start, n + 1):
            path.append(i)  # 选择当前数字
            backtrack(i + 1, path)  # 递归选择下一个数字
            path.pop()  # 撤销选择（回溯）
    
    result = []
    backtrack(1, [])
    return result

4. 复杂度分析

• 时间复杂度：O(C(n, k) * k)，其中 C(n, k) 是组合数，表示从 n 个数中选 k 个数的组合数。每个组合需要 O(k) 的时间来复制到结果集中。
• 空间复杂度：O(k)，递归栈的深度为 k。

5. 示例解释

示例 1：

输入：n = 4, k = 2

• 调用 backtrack(1, [])，开始递归：
  • 选择 1，递归调用 backtrack(2, [1])：
    • 选择 2，得到组合 [1, 2]。
    • 选择 3，得到组合 [1, 3]。
    • 选择 4，得到组合 [1, 4]。
  • 选择 2，递归调用 backtrack(3, [2])：
    • 选择 3，得到组合 [2, 3]。
    • 选择 4，得到组合 [2, 4]。
  • 选择 3，递归调用 backtrack(4, [3])：
    • 选择 4，得到组合 [3, 4]。
  • 选择 4，递归调用 backtrack(5, [4])，不满足条件，直接返回。
• 最终结果为 [[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]。

示例 2：

输入：n = 1, k = 1

• 调用 backtrack(1, [])，选择 1，得到组合 [1]。
• 最终结果为 [[1]]。

6. 总结

通过回溯法，我们可以高效地生成所有可能的组合。递归函数的设计和剪枝优化是解决问题的关键。

LC216. 组合总和 III

链接

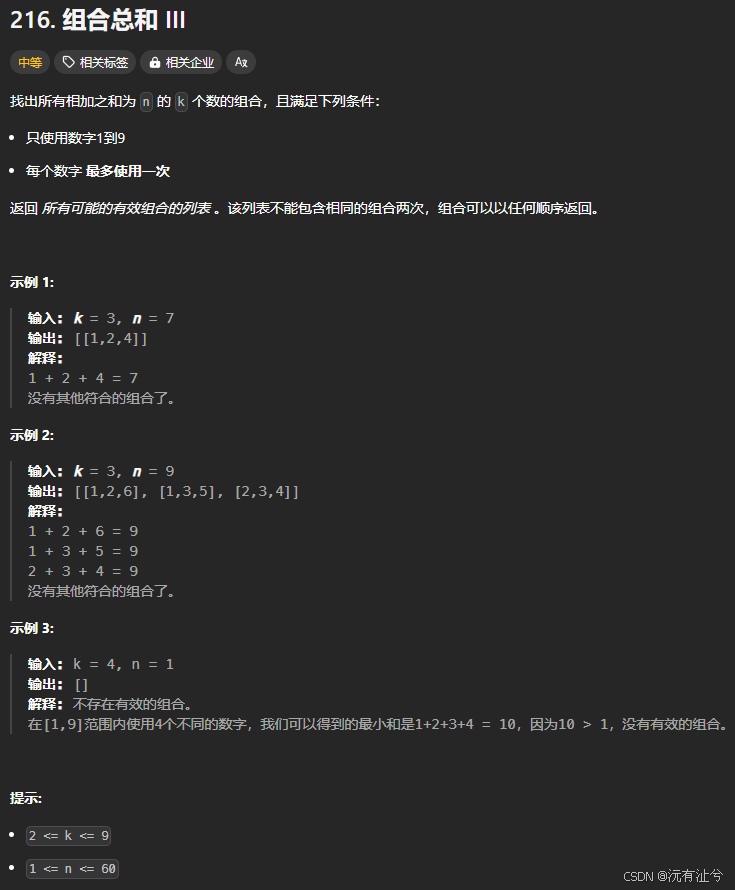
要解决这个问题，我们可以使用回溯算法来生成所有可能的组合。回溯算法是一种通过递归来探索所有可能的解决方案的方法，并在发现当前路径无法达到目标时进行回退。

具体步骤：

1. 定义递归函数：我们需要一个递归函数来生成所有可能的组合。这个函数将接收当前的组合、当前的起始数字、当前的数字和以及目标和 n 和组合长度 k。

2. 递归终止条件：

   • 如果当前组合的长度等于 k，并且当前数字和等于 n，则将当前组合加入结果列表。
   • 如果当前组合的长度大于 k 或者当前数字和大于 n，则直接返回。

3. 递归调用：从当前起始数字开始，依次尝试将每个数字加入当前组合，并递归调用函数。

4. 剪枝：为了减少不必要的计算，可以在递归调用时跳过那些不可能达到目标的数字。

代码实现：

def combinationSum3(k, n):
    def backtrack(start, k, n, path, res):
        if k == 0 and n == 0:
            res.append(path)
            return
        if k == 0 or n <= 0:
            return
        for i in range(start, 10):
            backtrack(i + 1, k - 1, n - i, path + [i], res)
    
    res = []
    backtrack(1, k, n, [], res)
    return res

# 示例测试
print(combinationSum3(3, 7))  # 输出: [[1, 2, 4]]
print(combinationSum3(3, 9))  # 输出: [[1, 2, 6], [1, 3, 5], [2, 3, 4]]
print(combinationSum3(4, 1))  # 输出: []

解释：

• backtrack 函数是递归的核心部分，它从 start 开始尝试将数字加入当前组合 path。
• k 表示还需要多少个数字，n 表示还需要达到的和。
• 当 k 为 0 且 n 为 0 时，表示找到了一个有效的组合，将其加入结果列表 res。
• 如果 k 为 0 或者 n 小于等于 0，则直接返回，不再继续递归。
• 在每次递归调用时，start 从当前数字的下一个数字开始，确保每个数字只使用一次。

复杂度分析：

• 时间复杂度：最坏情况下，我们需要遍历所有可能的组合，时间复杂度为 O(C(9, k))，其中 C(9, k) 是从 9 个数字中选取 k 个数字的组合数。
• 空间复杂度：递归栈的深度最多为 k，因此空间复杂度为 O(k)。

这个方法能够有效地找到所有满足条件的组合，并且避免了重复组合的出现。

---

LC17. 电话号码的字母组合

🧩 方法一：迭代法（队列思想）

这种方法通过逐步构建每个可能的组合，利用队列来存储中间结果，每次处理一个数字时，将现有结果与当前数字对应的所有字母进行组合，生成新的结果。

Python 实现

def letterCombinations(digits: str) -> list[str]:
    if not digits:
        return []
    
    mapping = {
        '2': 'abc',
        '3': 'def',
        '4': 'ghi',
        '5': 'jkl',
        '6': 'mno',
        '7': 'pqrs',
        '8': 'tuv',
        '9': 'wxyz'
    }
    
    result = ['']
    for digit in digits:
        current_chars = mapping[digit]
        temp = []
        for s in result:
            for c in current_chars:
                temp.append(s + c)
        result = temp  # 更新结果
    
    return result

JavaScript 实现

function letterCombinations(digits) {
    if (digits.length === 0) return [];
    const mapping = {
        '2': 'abc',
        '3': 'def',
        '4': 'ghi',
        '5': 'jkl',
        '6': 'mno',
        '7': 'pqrs',
        '8': 'tuv',
        '9': 'wxyz'
    };
    let result = [''];
    for (const digit of digits) {
        const currentChars = mapping[digit];
        const temp = [];
        for (const s of result) {
            for (const c of currentChars) {
                temp.push(s + c);
            }
        }
        result = temp;  // 更新结果
    }
    return result;
}

思路解析

1. 初始化映射表：将数字与对应的字母存入字典。
2. 处理空输入：直接返回空列表。
3. 迭代构建组合：
   • 初始时，结果列表为 ['']。
   • 遍历每个数字，取出对应的字母。
   • 对当前结果中的每个字符串，逐一拼接当前数字的每个字母，生成新结果。
4. 更新结果：每次处理完一个数字后，用新生成的组合替换旧结果。

---

🌟 方法二：回溯法（递归实现）

回溯法通过递归遍历所有可能的组合路径，当路径长度等于输入长度时，将路径加入结果。

Python 实现

def letterCombinations(digits: str) -> list[str]:
    if not digits:
        return []
    
    mapping = {
        '2': 'abc',
        '3': 'def',
        '4': 'ghi',
        '5': 'jkl',
        '6': 'mno',
        '7': 'pqrs',
        '8': 'tuv',
        '9': 'wxyz'
    }
    
    res = []
    def backtrack(index, path):
        if index == len(digits):
            res.append(''.join(path))
            return
        current_digit = digits[index]
        for c in mapping[current_digit]:
            path.append(c)
            backtrack(index + 1, path)
            path.pop()  # 回溯
    
    backtrack(0, [])
    return res

JavaScript 实现

function letterCombinations(digits) {
    if (digits.length === 0) return [];
    const mapping = {
        '2': 'abc',
        '3': 'def',
        '4': 'ghi',
        '5': 'jkl',
        '6': 'mno',
        '7': 'pqrs',
        '8': 'tuv',
        '9': 'wxyz'
    };
    const res = [];
    const backtrack = (index, path) => {
        if (index === digits.length) {
            res.push(path.join(''));
            return;
        }
        const currentDigit = digits[index];
        for (const c of mapping[currentDigit]) {
            path.push(c);
            backtrack(index + 1, path);
            path.pop();  // 回溯
        }
    };
    backtrack(0, []);
    return res;
}

思路解析

1. 递归终止条件：当路径长度等于输入长度时，将路径转为字符串存入结果。
2. 递归过程：
   • 当前处理到第 index 个数字。
   • 遍历该数字对应的所有字母，依次添加到路径中。
   • 递归处理下一个数字，完成后回溯（移除当前字母）。

---

⚡ 复杂度分析

• 时间复杂度：两种方法均为 O(3^N * 4^M)，其中 N 是输入中对应3字母的数字数量，M 是4字母的数字数量。
• 空间复杂度：O(K)，K 为最终结果的数量（所有组合数），迭代法的中间结果会占用 O(K) 空间，回溯法的递归栈深度为 O(L)（L 是输入长度））。

---

📊 方法对比

方法	优点	缺点
迭代法	代码简单，无递归栈溢出风险	中间结果占用较多内存
回溯法	内存占用更优（仅保存路径）	递归深度大时可能栈溢出

根据输入规模选择合适的实现方式即可！