leetcode 17 电话号码组合笛卡尔积

abant2

已于 2023-02-10 23:15:35 修改

阅读量334

点赞数 1

CC 4.0 BY-SA版权

分类专栏：队列文章标签： leetcode 深度优先算法

于 2021-07-24 15:22:14 首次发布

本文链接：https://blog.youkuaiyun.com/qq_39678022/article/details/119058872

队列专栏收录该内容

8 篇文章

订阅专栏

一道关于笛卡尔积的面试题，原题为LeetCode 17。错误地使用回溯法会导致问题，因为回溯适合全排列而笛卡尔积有重复状态。最佳解决方案是使用迭代加队列。此外，提供了DFS解法的代码，以及使用Map初始化的便利性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

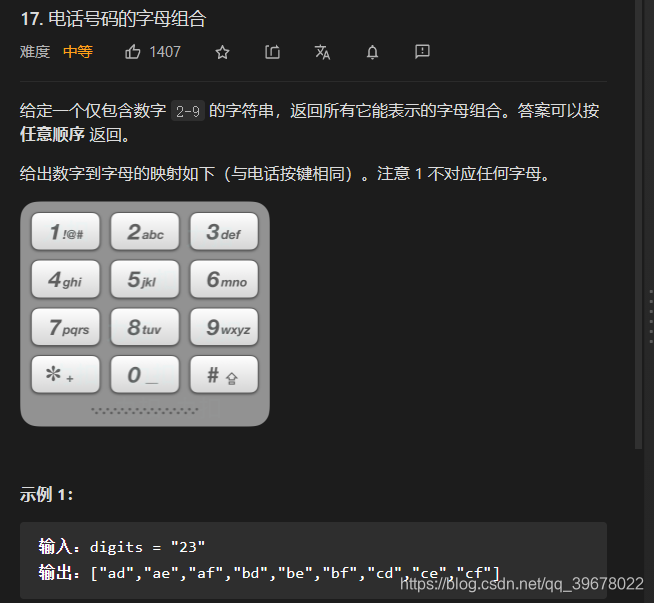
在这里插入图片描述
此题是面试遇见的一道题，当时出的是笛卡尔积，和这个其实道理是一样的。
此题如果用标准的回溯做，是会出问题的。一开始做的时候，我是把他当全排列做的。

但全排列是没有重复状态的，每次选一个。一个状态的前继状态只有一种可能。但笛卡尔积问题是不止一个前继状态，有重复节点就很难记录，所以此题采用迭代+队列来做是最好的。

class Solution {
public:
    vector<string> letterCombinations(string digits) {
        int n = digits.size();
        vector<string> ans;
        if(n == 0)return ans;
        vector<string> v{"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};

        queue<string> q;
        q.push("");

        for(auto d: digits)
        {
            int n = q.size();
            string cand = v[d-'2'];
            for(int i=0;i<n;i++)
            {
                string s = q.front(); q.pop();
                for(auto c: cand)
                {
                    q.push(s+c);
                }
            }
        }

        while(!q.empty())
        {
            ans.push_back(q.front());
            q.pop();
        }

        return ans;
    }
};

解法二：dfs
当时的我咋这么年轻呢，dfs都做这么久，直接上代码解决~ 此外，还有map的初始化方式，还是挺方便的。

class Solution {
map<int, string> m = {{2, "abc"}, {3, "def"}, {4, "ghi"}, {5, "jkl"}, 
    {6, "mno"}, {7, "pqrs"}, {8, "tuv"}, {9, "wxyz"}};
public:
    void dfs(vector<string>& ans, string tmp, string digits, int pos)
    {
        if(pos >= digits.size())
        {
            ans.push_back(tmp);
            return;
        }

        auto lst = m[digits[pos] - '0'];
        for(auto c: lst)
        {
            tmp += c;
            dfs(ans, tmp, digits, pos+1);
            tmp.pop_back();
        }
    }

    vector<string> letterCombinations(string digits) {
        vector<string> ans;
        if(digits.size() == 0)return ans;

        dfs(ans, "", digits, 0);

        return ans;
    }
};