leetcode 493 满足大小关系的对分治_关系大小推导 leedcode-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_39678022/article/details/115710001

本文探讨了如何使用分治策略和平衡二叉树数据结构来解决LeetCode中关于有序数组中的逆序对问题。两种方法对比，解析了平衡二叉树在迭代器操作上的局限性，并介绍了其他可能的解决方案如线段树和树状数组。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

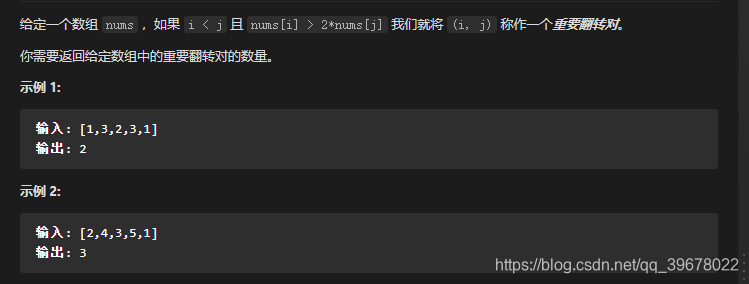
在这里插入图片描述

注：此题与327题很相似。
解法一：分治
直接考虑，如果是两个有序数组，O(N)能不能做，用单指针明显可以，同327题。故直接分治解决。

typedef long long ll;
class Solution {
public:
    void msort(vector<int>& nums, int& sum, int l, int r)
    {
        if(l == r)return;

        int mid = l + (r-l)/2;
        msort(nums, sum, l, mid);
        msort(nums, sum, mid+1, r);

        int p1 = mid+1;
        for(int p0=l;p0<=mid;p0++)
        {
            while(p1 <= r && nums[p0] > 2*(ll)nums[p1])p1++;
            sum += p1-mid-1;
        }
        inplace_merge(nums.begin()+l, nums.begin()+mid+1, nums.begin()+r+1);
    }

    int reversePairs(vector<int>& nums) {
        int ret = 0;
        msort(nums, ret, 0, nums.size()-1);
        return ret;
    }
};

解法二：平衡二叉树
由于要满足顺序关系，依然，分治能做，平衡二叉树也能做。

typedef long long ll;
class Solution {
public:
    int reversePairs(vector<int>& nums) {
        int ret = 0;
        multiset<ll> s;
        for(auto num: nums)
        {
            ll target = (ll)num*2 + 1;
            auto it = s.lower_bound(target);
            ret += distance(it, s.end());
            s.insert(num);
        }
        return ret;
    }
};