单链表、双向链表、循环链表、顺序栈、链栈、循环队列、链队列等算法理解与使用

已于 2025-05-16 16:25:45 修改
阅读量1.2k 收藏 31
点赞数 32
分类专栏： 算法 文章标签： 链表 算法 数据结构
于 2024-11-24 16:18:56 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_39411256/article/details/143656736
版权

一、简介

            轩哥此次整理了多种链表、堆栈、队列等知识，知识点较多，对于这些算法操作基本上都逃不过增删改查，因篇幅原因在每一章节的最后一算法进行操作，便于大家理解后，章节前面的自然水到渠成，通过图文代码实验方式逐步解析，希望对大家有一定的帮助，可以评论区留言逐一解答，同时也请大家多多指导。

二、链表

        2.1 简介：

                    链表用一组任意的存储单元来存放表中数据，存储每个元素a的同时还要存储其后元素a+1的存储空间形式，形成节点结构  [_data_|_next_] ; 其又分为静态和动态链表，静态链表特别的是节点的逻辑位置相邻元素其物理位置不一定相邻例如：data域为1 next地址却是5的；data域为5的next域却是2的依次装满一个静态链表。动态链表不需要估算个数分配空间，可以临时动态申请所需空间，根据需要申请与释放比较灵活。

        2.2 单链表：

                 2.2.1 原理：

                             一个节点有用数据域和指针域，为了单链表中所有结点都有一致的描述方式所以我们为它增加了一个头结点，data域不放数据或者只放表长内容，next域是a1的地址。

                 2.2.2 图解：

                              可见以下指针域总是指向下一个元素的数据域地址，这就是一条单链表形式。

                 2.2.3 代码：

                             代码使用尾插法建表，最后输入的数据是在后边另外还有头插法等这里只使用尾插法进行示例，用户输入数据结束后输出链表数据域值。

typedef struct node
{
	int data; //数据域
	struct node* next; //指针域

}linklist;
linklist* L; //节点指针

linklist* ceard(linklist* L);
void print(linklist* L);

void main()
{
	L = ceard(L); //建立单链表
	print(L); //输出链表元素
}
linklist* ceard(linklist* L)
{
	linklist* s, * H; //定义两个节点指针
	L = (linklist*)malloc(sizeof(linklist)); //首先为L链表申请空间
	L->next = NULL; //建立空链表
	H = L; //保护头节点
	int ch;
	scanf_s("%d", &ch); //用户输入数据
	while (ch != 999) // 如果输入的数据不是 999，则继续循环
	{
		s = (linklist*)malloc(sizeof(linklist)); // 为新节点申请空间
		s->data = ch; // 将用户输入的数据赋值给新节点的数据域
		s->next = NULL;  // 新节点的 next 指向 NULL
		H->next = s; // 当前链表的最后一个节点的 next 指向新节点
		H = s; // 更新 H 指针，使其指向新插入的节点
		scanf_s("%d", &ch); // 等待用户再次输入数据
	}
	return L;
}

void print(linklist* L)
{
	linklist* H;
	H = L;
	while (H->next != NULL)
	{
		H = H->next;
		printf("%d ", H->data); //输出链表数据
	}

}

                 2.2.4 实验现象：

                                输入一组数据并输入指定结束符可见建表成功后输出数值，尾插法每次输入的数据总从链表右侧插入，因此输出也为最后输出的值在右边。

        2.3 单循环链表：

                 2.3.1 原理：

                               本质上单循环链表就是一种头尾相接的链表，尾结点存放头结点形成一个环。

                 2.3.2 图解：

                                可见与单链表的区别仅仅首位相接。

                 2.3.3 代码：

                              通过用户输入一组数据建立单循环链表并输出。

typedef struct node {
	int data; // 数据域
	struct node* next; // 指针域
} linklist;

linklist* create(linklist* L); // 创建单循环链表
void print(linklist* L); // 输出链表元素

int main() {
	linklist* L = NULL; // 初始化节点指针
	L = create(L); // 建立单循环链表
	print(L); // 输出链表元素
	return 0;
}

linklist* create(linklist* L) {
	linklist* s, * H; // 定义两个节点指针
	L = (linklist*)malloc(sizeof(linklist)); // 首先为L链表申请空间
	if (!L) { // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	L->next = L; // 构建只有一个头节点的单循环链表
	H = L; // 保护头节点
	int ch;
	printf("请输入数据（输入999结束）：");
	scanf_s("%d", &ch); // 用户输入数据
	while (ch != 999) { // 如果输入的数据不是 999，则继续循环
		s = (linklist*)malloc(sizeof(linklist)); // 为新节点申请空间
		if (!s) { // 再次检查内存是否分配成功
			printf("内存分配失败\n");
			exit(1);
		}
		s->data = ch; // 将用户输入的数据赋值给新节点的数据域
		s->next = L; // 新节点的 next 指向头节点，形成循环
		H->next = s; // 当前链表的最后一个节点的 next 指向新节点
		H = s; // 更新 H 指针，使其指向新插入的节点
		printf("请输入数据（输入999结束）：");
		scanf_s("%d", &ch); // 等待用户再次输入数据
	}
	return L;
}

void print(linklist* L) {
	if (L == NULL || L->next == L) { // 判断链表是否为空
		printf("链表为空\n");
		return;
	}
	linklist* H = L->next; // 指向第一个有效节点
	do {
		printf("%d ", H->data); // 输出链表数据
		H = H->next; // 移动到下一个节点
	} while (H != L); // 当回到头节点时停止循环
	printf("\n");
}

                 2.3.4 实验现象：

                            create函数一直等待用户输入结束符结束后打印单循环链表数据。   

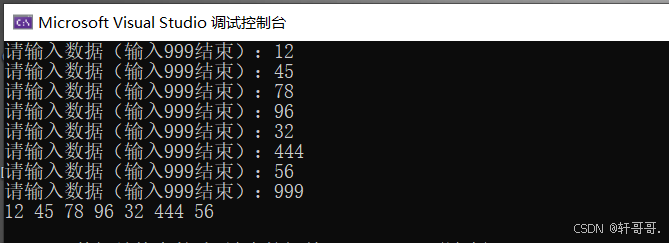
        2.4 双向循环链表：

                 2.4.1 原理：

                            原理是在普通结点的前屈增加一个指针域指向前屈结点的指针域，这样就能快速找到前屈结点，有了两条方向相反的链子   [ prior | data | next ]  = [ 前指针域 | 数据域 | 后指针域 ]

                 2.4.2 图解：

                          可见下图头结点的前指针域指向尾结点的后指针域形成循环，尾结点的后指针又指向头结点的前指针域形成了双循环，中间节点便相互头尾指针域相互指向。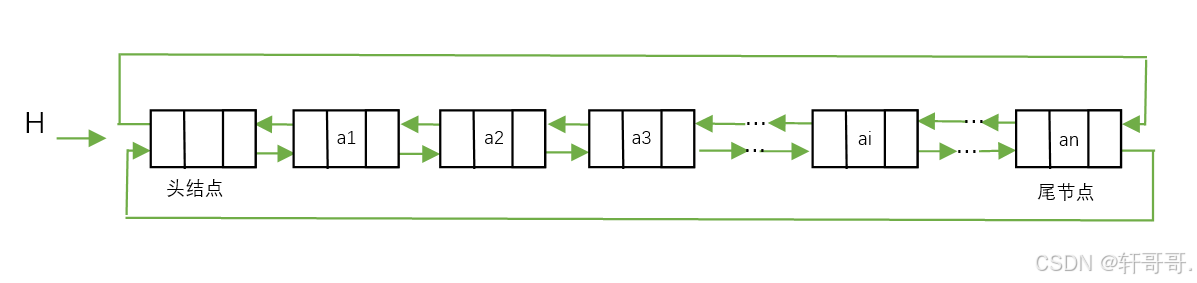     

                 2.4.3 代码：

                              首先创建空的双循环链表因为只有一个因此都是指向自己，然后插入值并输出还示例了修改值与删除节点、查找节点，对应增删改查操作。

// 定义双向循环链表的节点结构
typedef struct node {
	int data;       // 数据域
	struct node* prev; // 前向指针
	struct node* next; // 后向指针
} DLinkList;

// 创建双向循环链表
DLinkList* create() {
	DLinkList* L = (DLinkList*)malloc(sizeof(DLinkList)); // 分配头节点的内存
	if (!L) { // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	L->prev = L; // 头节点的前向指针指向自己
	L->next = L; // 头节点的后向指针指向自己
	return L; // 返回头节点
}

// 插入节点
void insert(DLinkList* L, int pos, int value) {
	if (pos < 1) { // 检查位置是否有效
		printf("位置无效\n");
		return;
	}
	DLinkList* p = L; // 从头节点开始
	int i;
	for (i = 1; i < pos && p->next != L; ++i) { // 遍历到指定位置
		p = p->next;
	}
	if (p->next == L && i < pos) { // 检查位置是否超出链表长度
		printf("位置超出链表长度\n");
		return;
	}
	DLinkList* newNode = (DLinkList*)malloc(sizeof(DLinkList)); // 分配新节点的内存
	if (!newNode) { // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	newNode->data = value; // 设置新节点的数据
	newNode->next = p->next; // 新节点的后向指针指向当前位置的下一个节点
	newNode->prev = p; // 新节点的前向指针指向当前位置
	p->next->prev = newNode; // 当前位置下一个节点的前向指针指向新节点
	p->next = newNode; // 当前位置的后向指针指向新节点
}

// 删除节点
void deletes(DLinkList* L, int pos) {
	if (pos < 1 || L->next == L) { // 检查位置是否有效或链表是否为空
		printf("位置无效或链表为空\n");
		return;
	}
	DLinkList* p = L; // 从头节点开始
	int i;
	for (i = 1; i < pos && p->next != L; ++i) { // 遍历到指定位置
		p = p->next;
	}
	if (p->next == L && i < pos) { // 检查位置是否超出链表长度
		printf("位置超出链表长度\n");
		return;
	}
	DLinkList* toDelete = p->next; // 获取要删除的节点
	p->next = toDelete->next; // 当前位置的后向指针指向要删除节点的下一个节点
	toDelete->next->prev = p; // 要删除节点的下一个节点的前向指针指向当前位置
	free(toDelete); // 释放要删除节点的内存
}

// 修改节点
void update(DLinkList* L, int pos, int value) {
	if (pos < 1 || L->next == L) { // 检查位置是否有效或链表是否为空
		printf("位置无效或链表为空\n");
		return;
	}
	DLinkList* p = L; // 从头节点开始
	int i;
	for (i = 1; i <= pos && p->next != L; ++i) { // 遍历到指定位置
		p = p->next;
	}
	if (p->next == L && i <= pos) { // 检查位置是否超出链表长度
		printf("位置超出链表长度\n");
		return;
	}
	p->data = value; // 修改节点的数据
}

// 查找节点
DLinkList* find(DLinkList* L, int value) {
	DLinkList* p = L->next; // 从头节点的下一个节点开始
	while (p != L) { // 遍历链表
		if (p->data == value) { // 如果找到匹配的节点
			return p; // 返回该节点
		}
		p = p->next; // 移动到下一个节点
	}
	return NULL; // 如果没有找到，返回NULL
}

// 打印链表
void print(DLinkList* L) {
	if (L->next == L) { // 检查链表是否为空
		printf("链表为空\n");
		return;
	}
	DLinkList* p = L->next; // 从头节点的下一个节点开始
	while (p != L) { // 遍历链表
		printf("%d ", p->data); // 打印节点数据
		p = p->next; // 移动到下一个节点
	}
	printf("\n"); // 换行
}

int main() {
	DLinkList* L = create(); // 创建双向循环链表

	insert(L, 1, 20); // 在位置1插入值10
	insert(L, 2, 10); // 在位置2插入值20
	insert(L, 3, 30); // 在位置3插入值30
	insert(L, 4, 16); // 在位置4插入值16
	print(L); // 打印链表

	update(L, 2, 25); // 修改位置2的值为25
	print(L); // 打印链表

	deletes(L, 2); // 删除位置2的节点
	print(L); // 打印链表

	DLinkList* found = find(L, 30); // 查找值为30的节点

	if (found != NULL) {
		printf("找到节点，数据为：%d\n", found->data); // 如果找到，打印节点数据
	}
	else {
		printf("未找到节点\n"); // 如果未找到，打印未找到
	}

	return 0; // 返回0表示程序正常结束
}

                 2.4.4 实验现象：

三、堆栈

        3.1 简介：

                    堆栈简称‘栈’，子弹夹型线性序列；“先进后出”，后进先出，因为a1无前继，an无后继，a1是a2唯一前屈… （LIFO）的数据结构，如下图符合子弹夹原理。

        3.2 顺序栈：

                 3.2.1 原理：

                            用地址连续的存储空间一次存储栈中的数据元素，并记录当前栈顶数据元素的位置，这样的栈称为顺序栈。

                 3.2.2 图解：

                            A为栈底，F为栈顶，出栈入栈从栈顶处操作，就像子弹夹。

                 3.2.3 代码：

                         以下展示了用户输入一组数据并输入指定字符结束后按堆栈特性先进后出，后进先出的特性进行打印数据。

#define maxlen 10  // 定义栈的最大容量为10

// 定义栈的结构体
typedef struct {
	int data[maxlen]; // 数据数组，用于存储栈中的元素
	int top;          // 栈顶指针，初始值为-1表示栈为空
} list;

list* S; // 定义栈指针

// 插入元素到栈中
void inser(list* S, int x) {
	S->top++; // 栈顶指针加1
	S->data[S->top] = x; // 将元素x存入栈顶位置
}

// 打印栈中的元素
void print(list* S) {
	while (S->top >= 0) { // 当栈顶指针大于等于0时，表示栈中还有元素
		printf("S->data[%d]=%d ", S->top - 1, S->data[S->top]); // 打印栈顶元素
		S->top--; // 栈顶指针减1，模拟出栈操作
	}
	printf("\r\n");
	printf("\r\n");
	printf("\r\n");
}

void main() {
	S = (list*)malloc(sizeof(list)); // 分配栈的内存
	S->top = -1; // 初始化栈顶指针为-1，表示栈为空

	int ch;
	scanf_s("%d", &ch); //用户输入数据
	while(ch!=999)
	{
		inser(S, ch); // 将读取的整数插入栈中
		scanf_s("%d", &ch); // 从用户输入读取一个整数
	}

	print(S); // 打印栈中的所有元素
}

                 3.2.4 实验现象：

                        用户输入45、62、12、45 并以999结束后打印。可见弹栈后一次输出的栈顶数据。

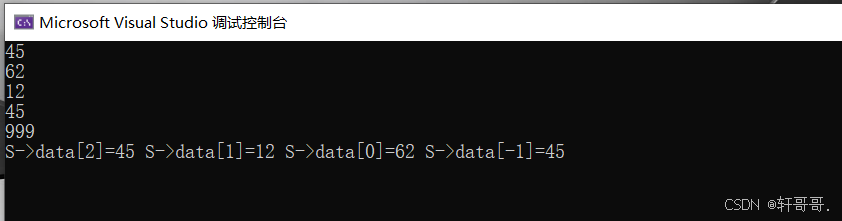
        3.3 链栈：

                 3.3.1 原理：

                              数据域的旁边加多一个指针域形成一个结点，指针域存放后继ai+1的存储地址，实际上它就是一个单链表，只是以堆栈特性去描述。

                 3.3.2 图解：

                 3.3.3 代码：

                            以下代码示例了堆栈的增删改查操作。    

// 定义链栈的节点结构
typedef struct node {
	int data;               // 数据域
	struct node* next;      // 指针域
} LinkStack;

LinkStack* LS;              // 定义链栈指针

// 创建链栈
LinkStack* createStack(LinkStack* LS) {
	LS = (LinkStack*)malloc(sizeof(LinkStack)); // 分配头节点的内存
	if (!LS) {                                  // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	LS->next = NULL;                            // 初始化头节点的指针域为NULL
	return LS;                                  // 返回头节点
}

// 插入元素到链栈中（入栈）
void push(LinkStack* LS, int data) {
	LinkStack* newNode = (LinkStack*)malloc(sizeof(LinkStack)); // 分配新节点的内存
	if (!newNode) {                                             // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	newNode->data = data;                                       // 设置新节点的数据
	newNode->next = LS->next;                                   // 新节点的指针域指向当前栈顶
	LS->next = newNode;                                         // 头节点的指针域指向新节点
}

// 删除链栈的栈顶元素（出栈）
int pop(LinkStack* LS) {
	if (LS->next == NULL) {                                     // 检查栈是否为空
		printf("栈为空，无法出栈\n");
		return -1;                                              // 返回-1表示出栈失败
	}
	LinkStack* toDelete = LS->next;                             // 获取栈顶节点
	int data = toDelete->data;                                  // 获取栈顶节点的数据
	LS->next = toDelete->next;                                  // 头节点的指针域指向新的栈顶
	free(toDelete);                                             // 释放栈顶节点的内存
	return data;                                                // 返回栈顶节点的数据
}

// 修改链栈中某个位置的元素
void update(LinkStack* LS, int pos, int newData) {
	if (pos < 1) {                                              // 检查位置是否有效
		printf("位置无效\n");
		return;
	}
	LinkStack* p = LS->next;                                    // 从栈顶开始
	int i;
	for (i = 1; i < pos && p != NULL; ++i) {                    // 遍历到指定位置
		p = p->next;
	}
	if (p == NULL) {                                            // 检查位置是否超出链栈长度
		printf("位置超出链栈长度\n");
		return;
	}
	p->data = newData;                                          // 修改指定位置的元素
}

// 查找链栈中某个值的位置
int find(LinkStack* LS, int value) {
	LinkStack* p = LS->next;                                    // 从栈顶开始
	int pos = 1;                                                // 初始化位置为1
	while (p != NULL) {                                         // 遍历链栈
		if (p->data == value) {                                 // 如果找到匹配的值
			return pos;                                         // 返回位置
		}
		p = p->next;                                            // 移动到下一个节点
		pos++;                                                  // 位置加1
	}
	return -1;                                                  // 如果未找到，返回-1
}

// 打印链栈
void print(LinkStack* LS) {
	if (LS->next == NULL) {                                     // 检查链栈是否为空
		printf("链栈为空\n");
		return;
	}
	LinkStack* p = LS->next;                                    // 从栈顶开始
	while (p != NULL) {                                         // 遍历链栈
		printf("%d ", p->data);                                 // 打印节点数据
		p = p->next;                                            // 移动到下一个节点
	}
	printf("\n");                                               // 换行
}

int main() {
	LS = createStack(LS);                                       // 创建链栈

	// 入栈操作
	push(LS, 10);                                               // 入栈10
	push(LS, 20);                                               // 入栈20
	push(LS, 30);                                               // 入栈30
	push(LS, 16);                                               // 入栈26
	push(LS, 23);                                               // 入栈23
	print(LS);                                                  // 打印链栈

	// 出栈操作
	int poppedValue = pop(LS);                                  // 出栈
	printf("出栈的值为：%d\n", poppedValue);                     // 打印出栈的值
	print(LS);                                                  // 打印链栈

	// 修改操作
	printf("修改栈顶的值为25\n");
	update(LS, 1, 25);                                          // 修改栈顶元素为25
	print(LS);                                                  // 打印链栈

	// 查找操作
	int position = find(LS, 10);                                // 查找值为10的元素
	if (position != -1) {
		printf("值为10的元素位于位置：%d\n", position);          // 如果找到，打印位置
	}
	else {
		printf("未找到值为25的元素\n");                          // 如果未找到，打印未找到
	}

	return 0;                                                   // 返回0表示程序正常结束
}

                 3.3.4 实验现象：

                                在代码中随意插入了5个值并打印可见遵循了子弹夹原理，并弹出栈顶好比用了一颗子弹，下一颗子弹成为了栈顶；修改栈顶的值再次打印，最后寻找元素打印。

四、队列

        4.1 简介：

                     队列定义：类似于一个管道，水先进来，也先出去；一般我们允许插入元素的一端称为队尾，允许删除元素的一端称为队头，因此队列是一种先进先出（FIFO）的数据结构。

        4.2 顺序队列：

                 4.2.1 原理：

                             插入与删除是在两端进行；所以使用2个变量记住头尾当前位置，队头指针（无论位置在哪总指队头指针），队尾指针（无论位置在哪总指队尾指针）。

                 4.2.2 图解：

                              规定fornt只允许出队，rear只允许入队，就像一根水管道，水流从右往左流动，从rear进水，fornt出水。

                 4.2.3 代码：

                                代码示例了顺序队列的出入队操作，本质上就是操作移动fornt与rear。

#define MAX_SIZE 10  // 定义队列的最大容量

// 定义顺序队列的结构
typedef struct {
	int data[MAX_SIZE];  // 数据数组，用于存储队列中的元素
	int front;           // 队首指针，指向队首元素的位置
	int rear;            // 队尾指针，指向队尾元素的下一个位置
} Queue;

Queue* Q;  // 定义队列指针

// 创建队列
Queue* createQueue() {
	Q = (Queue*)malloc(sizeof(Queue));  // 分配队列的内存
	if (!Q) {                           // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	Q->front = 0;                       // 初始化队首指针
	Q->rear = 0;                        // 初始化队尾指针
	return Q;                           // 返回队列
}

// 判断队列是否为空
int isEmpty(Queue* Q) {
	return Q->front == Q->rear;         // 如果队首指针等于队尾指针，表示队列为空
}

// 判断队列是否已满
int isFull(Queue* Q) {
	return (Q->rear + 1) % MAX_SIZE == Q->front;  // 如果队尾指针的下一个位置等于队首指针，表示队列已满
}

// 入队操作
void enqueue(Queue* Q, int data) {
	if (isFull(Q)) {                    // 检查队列是否已满
		printf("队列已满，无法入队\n");
		return;
	}
	Q->data[Q->rear] = data;            // 将数据存入队尾指针位置
	Q->rear = (Q->rear + 1) % MAX_SIZE; // 更新队尾指针，使用模运算实现循环队列
}

// 出队操作
int dequeue(Queue* Q) {
	if (isEmpty(Q)) {                   // 检查队列是否为空
		printf("队列为空，无法出队\n");
		return -1;                      // 返回-1表示出队失败
	}
	int data = Q->data[Q->front];       // 获取队首元素的数据
	Q->front = (Q->front + 1) % MAX_SIZE; // 更新队首指针，使用模运算实现循环队列
	return data;                        // 返回队首元素的数据
}

// 打印队列
void printQueue(Queue* Q) {
	if (isEmpty(Q)) {                   // 检查队列是否为空
		printf("队列为空\n");
		return;
	}
	int i = Q->front;
	while (i != Q->rear) {              // 遍历队列中的所有元素
		printf("%d ", Q->data[i]);      // 打印队列中的元素
		i = (i + 1) % MAX_SIZE;         // 更新索引，使用模运算实现循环队列
	}
	printf("\n");                       // 换行
}

int main() {
	Q = createQueue();                  // 创建队列

	// 入队操作
	enqueue(Q, 10);                     // 入队10
	enqueue(Q, 20);                     // 入队20
	enqueue(Q, 30);                     // 入队30
	printQueue(Q);                      // 打印队列

	// 出队操作
	int dequeuedValue = dequeue(Q);     // 出队
	if (dequeuedValue != -1) {
		printf("出队的值为：%d\n", dequeuedValue);  // 打印出队的值
	}
	printQueue(Q);                      // 打印队列

	// 再次入队
	printf("入队的值为: 40\r\n");
	enqueue(Q, 40);                     // 入队40
	printQueue(Q);                      // 打印队列

	return 0;                           // 返回0表示程序正常结束
}

                 4.2.4 实验现象：

                             首先代码中入队了三个数再出队一个数再入队一个数，完全遵循本次实验特性。

        4.3 循环队列：

                 4.3.1 原理：

                             通过对顺序队列的改进，使得队列的存储空间首尾相连，形成一个环状结构，从而更高效地利用存储空间。   

                 4.3.2 图解：

                              队头不断的删除，而队尾添加可以移动到队头的左边，充分利用了空间。

                 4.3.3 代码：

                         代码示例了循环队列的出入队操作，本质上就是操作移动fornt与rear。

#define MAX_SIZE 10  // 定义队列的最大容量

// 定义循环队列的结构
typedef struct {
	int data[MAX_SIZE];  // 数据数组，用于存储队列中的元素
	int front;           // 队首指针，指向队首元素的位置
	int rear;            // 队尾指针，指向队尾元素的下一个位置
} CircularQueue;

CircularQueue* Q;  // 定义队列指针

// 创建队列
CircularQueue* createQueue() {
	Q = (CircularQueue*)malloc(sizeof(CircularQueue));  // 分配队列的内存
	if (!Q) {                                           // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	Q->front = 0;                                       // 初始化队首指针
	Q->rear = 0;                                        // 初始化队尾指针
	return Q;                                           // 返回队列
}

// 判断队列是否为空
int isEmpty(CircularQueue* Q) {
	return Q->front == Q->rear;                         // 如果队首指针等于队尾指针，表示队列为空
}

// 判断队列是否已满
int isFull(CircularQueue* Q) {
	return (Q->rear + 1) % MAX_SIZE == Q->front;        // 如果队尾指针的下一个位置等于队首指针，表示队列已满
}

// 入队操作
void enqueue(CircularQueue* Q, int data) {
	if (isFull(Q)) {                                    // 检查队列是否已满
		printf("队列已满，无法入队\n");
		return;
	}
	Q->data[Q->rear] = data;                            // 将数据存入队尾指针位置
	Q->rear = (Q->rear + 1) % MAX_SIZE;                 // 更新队尾指针，使用模运算实现循环队列
}

// 出队操作
int dequeue(CircularQueue* Q) {
	if (isEmpty(Q)) {                                   // 检查队列是否为空
		printf("队列为空，无法出队\n");
		return -1;                                      // 返回-1表示出队失败
	}
	int data = Q->data[Q->front];                       // 获取队首元素的数据
	Q->front = (Q->front + 1) % MAX_SIZE;               // 更新队首指针，使用模运算实现循环队列
	return data;                                        // 返回队首元素的数据
}

// 打印队列
void printQueue(CircularQueue* Q) {
	if (isEmpty(Q)) {                                   // 检查队列是否为空
		printf("队列为空\n");
		return;
	}
	int i = Q->front;
	while (i != Q->rear) {                              // 遍历队列中的所有元素
		printf("%d ", Q->data[i]);                      // 打印队列中的元素
		i = (i + 1) % MAX_SIZE;                         // 更新索引，使用模运算实现循环队列
	}
	printf("\n");                                       // 换行
}

int main() {
	Q = createQueue();                                  // 创建队列

	// 入队操作
	enqueue(Q, 10);                                     // 入队10
	enqueue(Q, 20);                                     // 入队20
	enqueue(Q, 30);                                     // 入队30
	printQueue(Q);                                      // 打印队列

	// 出队操作
	int dequeuedValue = dequeue(Q);                     // 出队
	if (dequeuedValue != -1) {
		printf("出队的值为：%d\n", dequeuedValue);       // 打印出队的值
	}
	printQueue(Q);                                      // 打印队列

	// 再次入队
	printf("入队的值为: 40\r\n");
	enqueue(Q, 40);                                     // 入队40
	printQueue(Q);                                      // 打印队列

	return 0;                                           // 返回0表示程序正常结束
}

                 4.3.4 实验现象：

                             首先代码中入队了三个数再出队一个数再入队一个数，完全遵循本次实验特性。

        4.4  链队列：

                 4.4.1 原理：

                               链队列是一种使用链表实现的队列数据结构。与顺序队列相比，链队列没有固定大小的限制，可以动态扩展。

                 4.4.2 图解：

                               可见就是一个单链表遵循了FIFO的特性！！！

                 4.4.3 代码：

                             代码示例了链队列的出入队操作，本质上就是操作移动fornt与rear。

// 定义节点结构
typedef struct Node {
	int data;             // 数据域
	struct Node* next;    // 指针域，指向下一个节点
} Node;

// 定义链队列结构
typedef struct {
	Node* front;          // 队首指针，指向队首节点
	Node* rear;           // 队尾指针，指向队尾节点
} LinkedListQueue;

LinkedListQueue* Q;  // 定义队列指针

// 创建链队列
LinkedListQueue* createQueue() {
	Q = (LinkedListQueue*)malloc(sizeof(LinkedListQueue));  // 分配队列的内存
	if (!Q) {                                               // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	Q->front = NULL;                                         // 初始化队首指针
	Q->rear = NULL;                                          // 初始化队尾指针
	return Q;                                                // 返回队列
}

// 判断队列是否为空
int isEmpty(LinkedListQueue* Q) {
	return Q->front == NULL;                                 // 如果队首指针为NULL，表示队列为空
}

// 入队操作
void enqueue(LinkedListQueue* Q, int data) {
	Node* newNode = (Node*)malloc(sizeof(Node));             // 分配新节点的内存
	if (!newNode) {                                          // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	newNode->data = data;                                    // 设置新节点的数据
	newNode->next = NULL;                                    // 新节点的指针域初始化为NULL

	if (isEmpty(Q)) {                                        // 如果队列为空
		Q->front = newNode;                                  // 队首指针指向新节点
		Q->rear = newNode;                                   // 队尾指针指向新节点
	}
	else {
		Q->rear->next = newNode;                             // 当前队尾节点的指针域指向新节点
		Q->rear = newNode;                                   // 更新队尾指针
	}
}

// 出队操作
int dequeue(LinkedListQueue* Q) {
	if (isEmpty(Q)) {                                        // 检查队列是否为空
		printf("队列为空，无法出队\n");
		return -1;                                           // 返回-1表示出队失败
	}
	Node* toDelete = Q->front;                               // 获取队首节点
	int data = toDelete->data;                               // 获取队首节点的数据
	Q->front = Q->front->next;                               // 更新队首指针
	if (Q->front == NULL) {                                  // 如果队列变为空
		Q->rear = NULL;                                      // 队尾指针置为NULL
	}
	free(toDelete);                                          // 释放队首节点的内存
	return data;                                             // 返回队首节点的数据
}

// 打印队列
void printQueue(LinkedListQueue* Q) {
	if (isEmpty(Q)) {                                        // 检查队列是否为空
		printf("队列为空\n");
		return;
	}
	Node* p = Q->front;                                      // 从队首节点开始
	while (p != NULL) {                                      // 遍历链表
		printf("%d ", p->data);                              // 打印节点数据
		p = p->next;                                         // 移动到下一个节点
	}
	printf("\n");                                            // 换行
}

int main() {
	Q = createQueue();                                       // 创建队列

	// 入队操作
	enqueue(Q, 10);                                          // 入队10
	enqueue(Q, 20);                                          // 入队20
	enqueue(Q, 30);                                          // 入队30
	printQueue(Q);                                           // 打印队列

	// 出队操作
	int dequeuedValue = dequeue(Q);                          // 出队
	if (dequeuedValue != -1) {
		printf("出队的值为：%d\n", dequeuedValue);           // 打印出队的值
	}
	printQueue(Q);                                           // 打印队列

	// 再次入队
	printf("入队的值为: 40\r\n");
	enqueue(Q, 40);                                          // 入队40
	printQueue(Q);                                           // 打印队列

	return 0;                                                // 返回0表示程序正常结束
}

                 4.4.4 实验现象：

                             首先代码中入队了三个数再出队一个数再入队一个数，完全遵循本次实验特性。

        4.5 循环链队列：

                 4.5.1 原理：

                                使用链表实现的循环队列。与普通的链队列相比，链循环队列通过将队尾节点的 next 指针指向队首节点，形成一个环状结构，从而实现循环队列的功能。这种结构不仅具备链队列的优点，还能更高效地利用存储空间。

                 4.5.2 图解：

                              循环链队列形式。

                 4.5.3 代码：

                           代码示例了循环链队列的出入队操作，本质上就是操作移动fornt与rear。

// 定义节点结构
typedef struct Node {
	int data;             // 数据域
	struct Node* next;    // 指针域，指向下一个节点
} Node;

// 定义链循环队列结构
typedef struct {
	Node* front;          // 队首指针，指向队首节点
	Node* rear;           // 队尾指针，指向队尾节点
} CircularLinkedListQueue;

CircularLinkedListQueue* Q;  // 定义队列指针

// 创建链循环队列
CircularLinkedListQueue* createQueue() {
	Q = (CircularLinkedListQueue*)malloc(sizeof(CircularLinkedListQueue));  // 分配队列的内存
	if (!Q) {                                                               // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	Q->front = NULL;                                                         // 初始化队首指针
	Q->rear = NULL;                                                          // 初始化队尾指针
	return Q;                                                                // 返回队列
}

// 判断队列是否为空
int isEmpty(CircularLinkedListQueue* Q) {
	return Q->front == NULL;                                                 // 如果队首指针为NULL，表示队列为空
}

// 入队操作
void enqueue(CircularLinkedListQueue* Q, int data) {
	Node* newNode = (Node*)malloc(sizeof(Node));                             // 分配新节点的内存
	if (!newNode) {                                                          // 检查内存是否分配成功
		printf("内存分配失败\n");
		exit(1);
	}
	newNode->data = data;                                                    // 设置新节点的数据
	newNode->next = NULL;                                                    // 新节点的指针域初始化为NULL

	if (isEmpty(Q)) {                                                        // 如果队列为空
		Q->front = newNode;                                                  // 队首指针指向新节点
		Q->rear = newNode;                                                   // 队尾指针指向新节点
		newNode->next = Q->front;                                            // 形成环状结构
	}
	else {
		Q->rear->next = newNode;                                             // 当前队尾节点的指针域指向新节点
		Q->rear = newNode;                                                   // 更新队尾指针
		newNode->next = Q->front;                                            // 新节点的指针域指向队首节点，保持环状结构
	}
}

// 出队操作
int dequeue(CircularLinkedListQueue* Q) {
	if (isEmpty(Q)) {                                                        // 检查队列是否为空
		printf("队列为空，无法出队\n");
		return -1;                                                           // 返回-1表示出队失败
	}
	Node* toDelete = Q->front;                                               // 获取队首节点
	int data = toDelete->data;                                               // 获取队首节点的数据
	if (Q->front == Q->rear) {                                               // 如果队列只有一个节点
		Q->front = NULL;                                                     // 队首指针置为NULL
		Q->rear = NULL;                                                      // 队尾指针置为NULL
	}
	else {
		Q->front = Q->front->next;                                           // 更新队首指针
		Q->rear->next = Q->front;                                            // 更新队尾节点的指针域，保持环状结构
	}
	free(toDelete);                                                          // 释放队首节点的内存
	return data;                                                             // 返回队首节点的数据
}

// 打印队列
void printQueue(CircularLinkedListQueue* Q) {
	if (isEmpty(Q)) {                                                        // 检查队列是否为空
		printf("队列为空\n");
		return;
	}
	Node* p = Q->front;                                                      // 从队首节点开始
	do {
		printf("%d ", p->data);                                              // 打印节点数据
		p = p->next;                                                         // 移动到下一个节点
	} while (p != Q->front);                                                 // 循环直到回到队首节点
	printf("\n");                                                            // 换行
}

int main() {
	Q = createQueue();                                                       // 创建队列

	// 入队操作
	enqueue(Q, 10);                                                          // 入队10
	enqueue(Q, 20);                                                          // 入队20
	enqueue(Q, 30);                                                          // 入队30
	printQueue(Q);                                                           // 打印队列

	// 出队操作
	int dequeuedValue = dequeue(Q);                                          // 出队
	if (dequeuedValue != -1) {
		printf("出队的值为：%d\n", dequeuedValue);                           // 打印出队的值
	}
	printQueue(Q);                                                           // 打印队列

	// 再次入队
	printf("入队的值为: 40\r\n");
	enqueue(Q, 40);                                                          // 入队40
	printQueue(Q);                                                           // 打印队列

	return 0;                                                                // 返回0表示程序正常结束
}

                 4.5.4 实验现象：

                             首先代码中入队了三个数再出队一个数再入队一个数，完全遵循本次实验特性。

五、结论

              通过以上理解可见，本质上有不少内容的数据结构是大差不差的，只是它们规则的与使用的方式、应用不同，在实际解决问题可以以此基本算法参考变换。

 

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值