本文详细介绍了次梯度的概念及其在凸函数中的应用。包括次梯度的存在性、性质及计算规则等内容，并通过实例帮助理解。
一：次梯度的定义
次梯度定义：设 f f f为适当凸函数， x x x为定义域 d o m f dom f domf中的一点，若向量 g ∈ R n g\in R^{n} g∈Rn，满足
f ( y ) ≥ f ( x ) + g T ( y − x ) , ∀ y ∈ d o m f f(y)\geq f(x)+g^{T}(y-x),\quad \forall y\in domf f(y)≥f(x)+gT(y−x),∀y∈domf
则称 g g g为函数 f f f在点 x x x的一个次梯度。进一步地，称集合
∂ f ( x ) = { g ∣ g ∈ R n , f ( y ) ≥ f ( x ) + g T ( y − x ) , ∀ y ∈ d o m f } \partial f(x)=\{g|g\in R^{n},f(y)\geq f(x)+g^{T}(y-x),\quad \forall y\in domf\} ∂f(x)={g∣g∈Rn,f(y)≥f(x)+gT(y−x),∀y∈domf}
为 f f f在点 x x x处的次微分
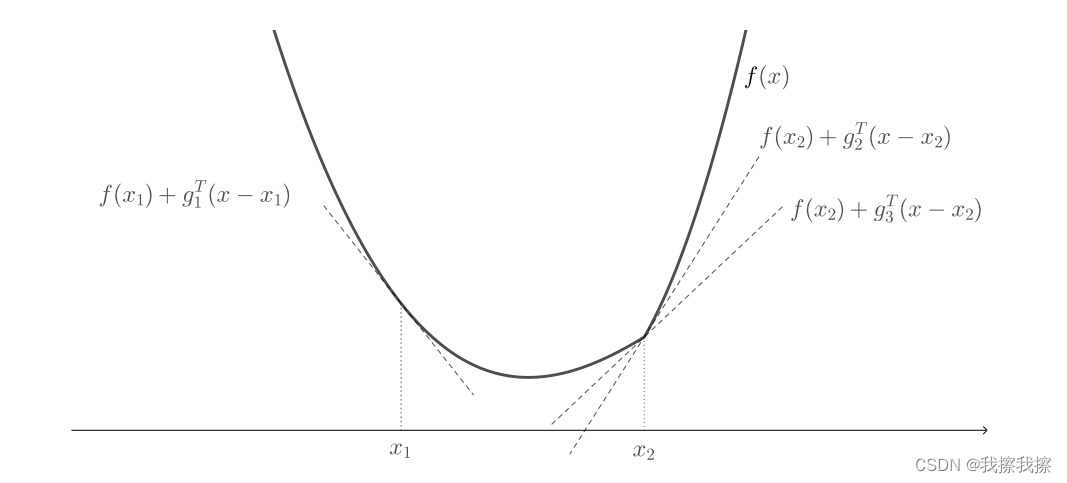
如下图
- g 1 g_{1} g1是点 x 1 x_{1} x1处的次梯度
-
g
2
g_{2}
g2、
g
3
g_{3}
g3是点
x
2
x_{2}
x2的次梯度
实际上，次梯度实际上借鉴了凸函数判定定理的一阶条件。所以定义次梯度的初衷之一也是希望它具有类似于梯度的一些性质
- 一阶条件：对于定义在凸集上的可微函数 f f f， f f f为凸函数当前仅当 f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) ∀ x , y ∈ d o m f f(y)\geq f(x)+\nabla f(x)^{T}(y-x) \quad \forall x,y\in domf f(y)≥f(x)+∇f(x)T(y−x)∀x,y∈domf
另外，从次梯度的定义可直接推出，若 g g g是 f ( x ) f(x) f(x)在 x 0 x_{0} x0处的次梯度，则函数
l ( x ) = f ( x 0 ) + g T ( x − x 0 ) l(x)=f(x_{0})+g^{T}(x-x_{0}) l(x)=f(x0)+gT(x−x0)
为凸函数 f ( x ) f(x) f(x)的一个全局下界。此外，次梯度 g g g可以诱导出上方图 e p i f epif epif在点 ( x , f ( x ) ) (x, f(x)) (x,f(x))处的一个支撑超平面
- 容易验证，对
e
p
i
f
epi f
epif中的任意点
(
y
,
t
)
(y, t)
(y,t)，有：
二：次梯度存在性
次梯度存在性：设 f f f为凸函数， d o m f dom f domf为其定义域。如果 x ∈ i n t d o m f x\in int domf x∈intdomf，则 ∂ f ( x ) \partial f(x) ∂f(x)是非空的。其中 i n t d o m f int domf intdomf的含义时集合 d o m f dom f domf的所有内点
证明：考虑 f ( x ) f(x) f(x)的上方图 e p i f epi f epif，由于 ( x , f ( x ) ) (x, f(x)) (x,f(x))是 e p i f epi f epif边界上的点，且 e p i f epi f epif为凸集，根据支撑超平面定理，存在 a ∈ R n , b ∈ R a\in R^{n},b\in R a∈Rn,b∈R使得
也即
a T ( y − x ) ≤ b ( f ( x ) − t ) a^{T}(y-x)\leq b(f(x)-t) aT(y−x)≤b(f(x)−t)
令 t → ∞ t\rightarrow \infty t→∞，可知上式成立的必要条件 b ≤ 0 b\leq0 b≤0，同时由于 x x x是内点，因此当取 y = x + ξ a ∈ d o m f y=x+\xi a\in dom f y=x+ξa∈domf, ξ > 0 \xi>0 ξ>0时， b = 0 b=0 b=0不能使得上式成立。于是令 g = − a b g=-\frac{a}{b} g=−ba，则对任意 y ∈ d o m f y\in domf y∈domf，有
g T ( y − x ) = a T ( y − x ) − b ≤ − ( f ( x ) − f ( y ) ) g^{T}(y-x)=\frac{a^{T}(y-x)}{-b}\leq-(f(x)-f(y)) gT(y−x)=−baT(y−x)≤−(f(x)−f(y))
即
f ( y ) ≥ f ( x ) + g T ( y − x ) f(y)\geq f(x)+g^{T}(y-x) f(y)≥f(x)+gT(y−x)
这说明 g g g是 f f f在点 x x x处的次梯度
例子：
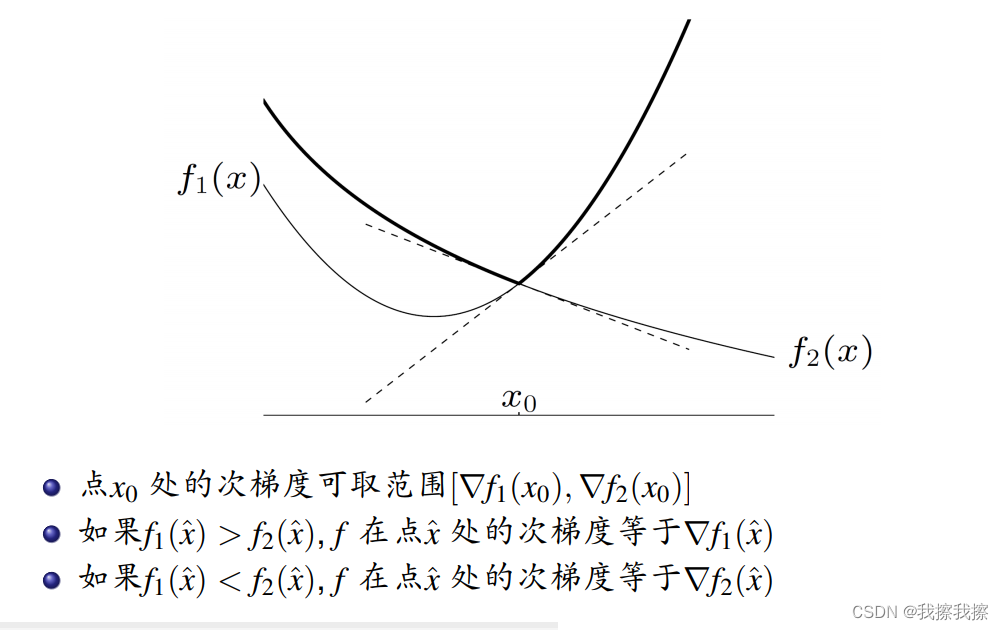
①： f ( x ) = m a x { f 1 ( x ) , f 2 ( x ) } f(x)=max\{f_{1}(x), f_{2}(x)\} f(x)=max{f1(x),f2(x)}, f 1 f_{1} f1， f 2 f_{2} f2是可微凸函数
②：绝对值函数 f ( x ) = ∣ x ∣ f(x)=|x| f(x)=∣x∣
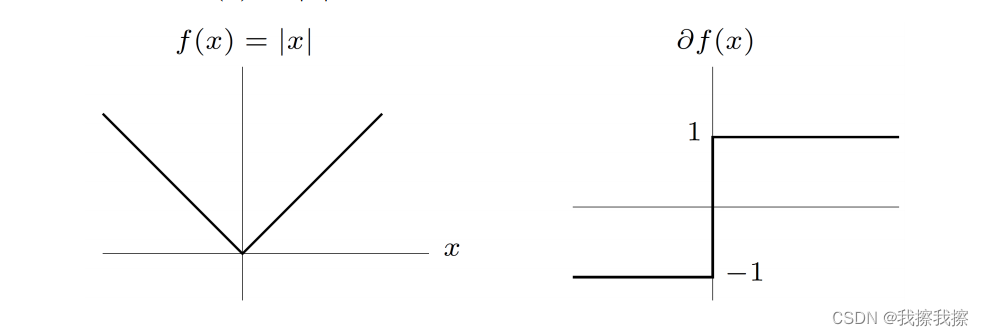
③：欧几里得范数 f ( x ) = ∣ ∣ x ∣ ∣ 2 f(x)=||x||_{2} f(x)=∣∣x∣∣2
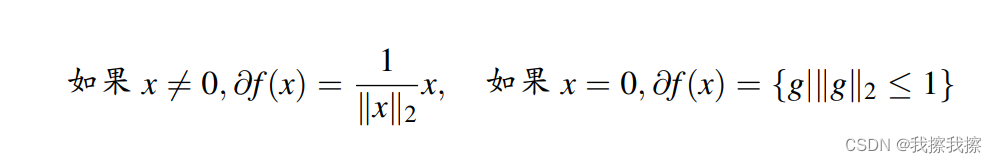
三：次梯度的性质
次梯度的性质：设 f f f是凸函数，则 ∂ f ( x ) \partial f(x) ∂f(x)有如下性质
- 次微分是凸集：对于任何 x ∈ d o m f x\in domf x∈domf， ∂ f ( x ) \partial f(x) ∂f(x)是一个闭凸集（可能为空集）
- 内点的次微分非空有界：对于任何 x ∈ d o m f x\in domf x∈domf， ∂ f ( x ) \partial f(x) ∂f(x)非空有界集
- 可微函数次微分：设凸函数 f ( x ) f(x) f(x)在 x 0 ∈ i n t d o m f x_{0}\in int domf x0∈intdomf处可微，则 ∂ f ( x 0 ) = { ∇ f ( x 0 ) } \partial f(x_{0})=\{\nabla f(x_{0})\} ∂f(x0)={∇f(x0)}
- 次梯度单调性：设 f : R n → R f:R^{n}\rightarrow R f:Rn→R为凸函数， x , y ∈ d o m f x,y\in domf x,y∈domf，则 ( u − v ) T ( x − y ) ≥ 0 (u-v)^{T}(x-y)\geq 0 (u−v)T(x−y)≥0，其中 u ∈ ∂ f ( x ) , v ∈ ∂ f ( y ) u\in\partial f(x),v\in\partial f(y) u∈∂f(x),v∈∂f(y)
- 次梯度连续性：设 f ( x ) f(x) f(x)是闭凸函数且 ∂ f \partial f ∂f在点 x ˉ \bar{x} xˉ附近存在且非空。若序列 x k → x ˉ x^{k} \rightarrow \bar{x} xk→xˉ， g k ∈ ∂ f ( x k ) g^{k}\in\partial f(x^{k}) gk∈∂f(xk)在点 x k x^{k} xk处的次梯度，且 g k → g ˉ g^{k}\rightarrow \bar{g} gk→gˉ，则 g ˉ ∈ ∂ f ( x ˉ ) \bar{g}\in\partial f(\bar{x}) gˉ∈∂f(xˉ)
四：凸函数的方向导数
在数学分析中，方向导数被定义为：设 f f f为适当函数，给定点 x 0 x_{0} x0以及方向 d ∈ R n d\in R^{n} d∈Rn，方向导数（若存在）定义为
l i m t ↓ 0 ϕ ( t ) = l i m t ↓ 0 f ( x 0 + t d ) − f ( x 0 ) t \mathop{lim}\limits_{t \downarrow 0}\phi (t)=\mathop{lim}\limits_{t \downarrow 0}\frac{f(x_{0}+td)-f(x_{0})}{t} t↓0limϕ(t)=t↓0limtf(x0+td)−f(x0)
其中 t ↓ 0 t \downarrow 0 t↓0表示 t t t单调下降趋于0.对于凸函数 f ( x ) f(x) f(x)，易知 ϕ ( t ) \phi (t) ϕ(t)在 ( 0 , + ∞ ) (0, +\infty) (0,+∞)上是单调不减，上式中的 l i m lim lim可以替换为下确界 i n f inf inf，上述此时极限总是存在（可以为无穷），进而凸函数总是可以定义为方向导数
方向导数：对于凸函数 f f f，给顶点 x 0 ∈ d o m f x_{0}\in domf x0∈domf以及方向 d ∈ R n d\in R^{n} d∈Rn，其方向导数定义为
∂ f ( x 0 ; d ) = i n f t > 0 f ( x 0 + t d ) − f ( x 0 ) t \partial f(x_{0};d)=\mathop{inf}\limits_{t>0}\frac{f(x_{0}+td)-f(x_{0})}{t} ∂f(x0;d)=t>0inftf(x0+td)−f(x0)
方向导数可能是正负无穷，但是在定义域内点处方向导数 ∂ f ( x 0 ; d ) \partial f(x_{0};d) ∂f(x0;d)是有限的
方向导数和次梯度：设 f : R n → ( − ∞ , + ∞ ] f:R^{n}\rightarrow(-\infty,+\infty] f:Rn→(−∞,+∞]为凸函数，点 x 0 ∈ i n t d o m f x_{0}\in int domf x0∈intdomf， d d d为 R n R^{n} Rn中任一方向，则
- 对于可微函数： ∂ f ( x 0 ; d ) = ∇ f ( x 0 T ) d \partial f(x_{0};d)=\nabla f(x_{0}^{T})d ∂f(x0;d)=∇f(x0T)d
- 这也说明 ∂ f ( x 0 ; d ) \partial f(x_{0};d) ∂f(x0;d)对所有的 x 0 ∈ i n t d o m f x_{0}\in int domf x0∈intdomf，以及所有的 d d d都存在
∂ f ( x 0 ; d ) = m a x g ∈ ∂ f ( x 0 ) g T d \partial f(x_{0};d)=\mathop{max}\limits_{g\in \partial f(x_{0})}g^{T}d ∂f(x0;d)=g∈∂f(x0)maxgTd
作更为一般的推导：设 f f f为适当凸函数，且在 x 0 x_{0} x0处次微分不为空集，则对任意 d ∈ R n d\in R^{n} d∈Rn，有
∂ f ( x 0 ; d ) = s u p g ∈ ∂ f ( x 0 ) g T d \partial f(x_{0};d)=\mathop{sup}\limits_{g\in \partial f(x_{0})}g^{T}d ∂f(x0;d)=g∈∂f(x0)supgTd
且当 ∂ f ( x 0 ; d ) \partial f(x_{0};d) ∂f(x0;d)不为无穷时，上确界可以取到
五：次梯度计算规则
次梯度计算：计算一个不可微凸函数的次梯度在优化算法设计中是很重要的问题，但根据定义来计算次梯度又比较繁琐，所以需要介绍一些次梯度的计算规则。需要注意次梯度计算分为
- 弱次梯度计算：得到一个次梯度即可，这足以满足大多数不可微凸函数优化算法；如果可以获得任意一点处 f ( x ) f(x) f(x)的值，那么总可以计算一个次梯度
- 强次梯度计算：得到 ∂ f ( x ) \partial f(x) ∂f(x)即所有次梯度，一些算法可能需要完整的次微分，计算可能相当负责
下面的介绍中，假设 x ∈ i n t d o m f x\in intdomf x∈intdomf
（1）基本规则
基本规则
- 可微凸函数：设 f f f为凸函数，若 f f f在点 x x x处可微，则 ∂ f ( x ) = { ∇ f ( x ) } \partial f(x)=\{\nabla f(x)\} ∂f(x)={∇f(x)}
- 凸函数的非负线性组合：设 f 1 f_{1} f1, f 2 f_{2} f2为凸函数，且满足 i n t d o m f 1 ∩ d o m f 2 ≠ ∅ int \quad domf_{1}\cap domf_{2}\neq \empty intdomf1∩domf2=∅，而 x ∈ d o m f 1 ∩ d o m f 2 x\in dom f_{1}\cap dom f_{2} x∈domf1∩domf2，若 f ( x ) = α 1 f 1 ( x ) + α 2 f 2 ( x ) , α 1 , α 2 ≥ 0 f(x)=\alpha_{1}f_{1}(x)+\alpha_{2}f_{2}(x),\alpha_{1},\alpha_{2}\geq 0 f(x)=α1f1(x)+α2f2(x),α1,α2≥0，则 f ( x ) f(x) f(x)的次微分： ∂ f ( x ) = α 1 ∂ f 1 ( x ) + α 2 ∂ f 2 ( x ) \partial f(x)=\alpha_{1}\partial f_{1}(x)+\alpha_{2}\partial f_{2}(x) ∂f(x)=α1∂f1(x)+α2∂f2(x)
- 线性变量替换：设 h h h为适当凸函数，且函数 f f f满足 f ( x ) = h ( A x + b ) , ∀ x ∈ R m f(x)=h(Ax+b),\forall x\in R^{m} f(x)=h(Ax+b),∀x∈Rm，其中 A ∈ R n × m A\in R^{n×m} A∈Rn×m， b ∈ R n b\in R^{n} b∈Rn。若存在 x # ∈ R m x^{\#}\in R^{m} x#∈Rm，使得 A x # + b ∈ i n t d o m h Ax^{\#}+b\in intdomh Ax#+b∈intdomh，则 ∂ f ( x ) = A T ∂ h ( A x + b ) \partial f(x)=A^{T}\partial h(Ax+b) ∂f(x)=AT∂h(Ax+b)， ∀ x ∈ i n t d o m f \forall x\in int domf ∀x∈intdomf
（2）两个函数之和的次梯度
Moreau-Rockafellar定理：设 f 1 , f 2 : R n → ( − ∞ , + ∞ ] f_{1},f_{2}:R^{n}\rightarrow(-\infty,+\infty] f1,f2:Rn→(−∞,+∞]是两个凸函数，则对任意的 x 0 ∈ R n x_{0}\in R^{n} x0∈Rn
∂ f 1 ( x 0 ) + ∂ f 2 ( x 0 ) ⊆ ∂ ( f 1 + f 2 ) ( x 0 ) \partial f_{1}(x_{0})+\partial f_{2}(x_{0}) \subseteq \partial(f_{1}+f_{2})(x_{0}) ∂f1(x0)+∂f2(x0)⊆∂(f1+f2)(x0)
进一步，若 i n t d o m f 1 ∩ d o m f 2 ≠ ∅ int\quad domf_{1}\cap domf_{2}\neq \empty intdomf1∩domf2=∅，则对任意 x 0 ∈ R n x_{0}\in R^{n} x0∈Rn
∂ ( f 1 + f 2 ) ( x 0 ) = ∂ f 1 ( x 0 ) + ∂ f 2 ( x 0 ) \partial(f_{1}+f_{2})(x_{0})=\partial f_{1}(x_{0})+\partial f_{2}(x_{0}) ∂(f1+f2)(x0)=∂f1(x0)+∂f2(x0)
（3）函数族的上确界
函数族的上确界：容易验证一族凸函数的上确界函数仍为凸函数。设 f 1 , f 2 , . . . , f m : R n → ( − ∞ , + ∞ ] f_{1},f_{2},...,f_{m}:R^{n}\rightarrow(-\infty,+\infty] f1,f2,...,fm:Rn→(−∞,+∞]均为凸函数，令
f ( x ) = m a x { f 1 ( x ) , f 2 ( x ) , . . . , f m ( x ) } , ∀ x ∈ R n f(x)=max\{f_{1}(x),f_{2}(x),...,f_{m}(x)\},\forall x\in R^{n} f(x)=max{f1(x),f2(x),...,fm(x)},∀x∈Rn
对 x 0 ∈ ∩ i = 1 m i n t d o m f i x_{0}\in \mathop{\cap}\limits_{i=1}^{m}int \quad domf_{i} x0∈i=1∩mintdomfi，定义 I ( x 0 ) = { i ∣ f i ( x 0 ) = f ( x 0 ) } I(x_{0})=\{i|f_{i}(x_{0})=f(x_{0})\} I(x0)={i∣fi(x0)=f(x0)}，则
∂ f ( x 0 ) = c o n v ∪ i ∈ I ( x 0 ) ∂ f i ( x 0 ) \partial f(x_{0})=conv \mathop{\cup}\limits_{i\in I(x_{0})}\partial f_{i}(x_{0}) ∂f(x0)=convi∈I(x0)∪∂fi(x0)
（4）固定分量的函数极小值
- 设 h : R n × R m → ( − ∞ , + ∞ ] h:R^{n}×R^{m}\rightarrow(-\infty, +\infty] h:Rn×Rm→(−∞,+∞]是关于 ( x , y ) (x,y) (x,y)的凸函数，则 f ( x ) = inf y h ( x , y ) f(x)=\mathop{\inf}\limits_{y}h(x,y) f(x)=yinfh(x,y)是关于 x ∈ R n x\in R^{n} x∈Rn的凸函数，以下结果可以用于求解 f f f在点 x x x的一个次梯度
固定分量的函数极小值：考虑函数 f ( x ) = inf y h ( x , y ) f(x)=\mathop{\inf}\limits_{y}h(x,y) f(x)=yinfh(x,y)，其中 h : R n × R m → ( − ∞ , + ∞ ] h:R^{n}×R^{m}\rightarrow(-\infty, +\infty] h:Rn×Rm→(−∞,+∞]是关于 ( x , y ) (x,y) (x,y)的凸函数。对 x ∗ ∈ R n \mathop{x}\limits^{*}\in R^{n} x∗∈Rn，设 y ∗ ∈ R m \mathop{y}\limits^{*}\in R^{m} y∗∈Rm满足 h ( x ∗ , y ∗ ) = f ( x ∗ ) h(\mathop{x}\limits^{*}, \mathop{y}\limits^{*})=f(\mathop{x}\limits^{*}) h(x∗,y∗)=f(x∗)，且存在 g ∈ R n g\in R^{n} g∈Rn，使得 ( g , 0 ) ∈ ∂ h ( x ∗ , y ∗ ) (g, 0)\in \partial h(\mathop{x}\limits^{*}, \mathop{y}\limits^{*}) (g,0)∈∂h(x∗,y∗)，则 g ∈ ∂ f ( x ∗ ) g\in \partial f(\mathop{x}\limits^{*}) g∈∂f(x∗)
（5）复合函数
复合函数：设 f 1 , f 2 , . . . , f m : R n → ( − ∞ , + ∞ ] f_{1},f_{2},...,f_{m}:R^{n}\rightarrow(-\infty,+\infty] f1,f2,...,fm:Rn→(−∞,+∞]为 m m m个凸函数， h : R m → ( − ∞ , + ∞ ] h:R^{m}\rightarrow(-\infty,+\infty] h:Rm→(−∞,+∞]为关于各分量单调递增的凸函数，令
f ( x ) = h ( f 1 ( x ) , f 2 ( x ) , . . . , f m ( x ) ) f(x)=h(f_{1}(x),f_{2}(x),...,f_{m}(x)) f(x)=h(f1(x),f2(x),...,fm(x))
设 z = ( z 1 , z 2 , . . . , z m ) ∈ ∂ h ( f 1 ( x ∗ ) , f 2 ( x ∗ ) , . . . , f m ( x ∗ ) ) z=(z_{1},z_{2},...,z_{m})\in \partial h(f_{1}(\mathop{x}\limits^{*}), f_{2}(\mathop{x}\limits^{*}),...,f_{m}(\mathop{x}\limits^{*})) z=(z1,z2,...,zm)∈∂h(f1(x∗),f2(x∗),...,fm(x∗))以及 g i ∈ ∂ f i ( x ∗ ) g_{i}\in\partial f_{i}(\mathop{x}\limits^{*}) gi∈∂fi(x∗)，则
g = z 1 g 1 + z 2 g 2 + . . . + z m g m ∈ ∂ f ( x ∗ ) g = z_{1}g_{1}+z_{2}g_{2}+...+z_{m}g_{m}\in \partial f(\mathop{x}\limits^{*}) g=z1g1+z2g2+...+zmgm∈∂f(x∗)
扫一扫
1132
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
