递归(Recursion)

 

目录

递归（Recursion）

实例分析

递归的基本思想

递归的使用规则

算法 – 斐波那契数列

fib函数的调用过程

斐波那契数优化1 – 记忆化

斐波那契数优化2

斐波那契数优化3

斐波那契数优化4 – 位运算取代模运算

斐波那契数优化5

算法 – 上楼梯（跳台阶）

问题

思路

代码

算法 – 汉诺塔（Hanoi）

问题

情景1 – 1个盘子

情景2 – 2个盘子

情景3 – 3个盘子

汉诺塔 – 递归思路

汉诺塔 – 实现

递归转非递归

递归转非递归方法

尾调用（Tail Call）

尾调用优化（Tail Call Optimization）

尾调用优化前的汇编代码（C++）

尾调用优化后的汇编代码（C++）

尾递归示例

---

递归（Recursion）

递归: 函数(方法)直接或间接调用自身

函数的调用过程

                             

函数的递归调用过程

                         

如果递归调用没有终止, 将会一直消耗栈空间, 最终导致栈内存溢出(Stack Overflow), 所以必需要有一个明确的结束递归的条件, 也叫作边界条件、递归基

实例分析

求 1+2+3+...+(n-1)+n 的和 (n>0)

实例1:

总消耗时间 T(n)= T(n−1)+O(1), 因此: 时间复杂度:O(n), 空间复杂度:O(n)

实例2:

时间复杂度: O(n), 空间复杂度: O(1)

实例3:

时间复杂度: O(1), 空间复杂度: O(1)

注意: 使用递归不是为了求得最优解, 是为了简化解决问题的思路, 代码会更加简洁; 递归求出来的很有可能不是最优解, 也有可能是最优解

递归的基本思想

拆解问题
把规模大的问题变成规模较小的同类型问题
规模较小的问题又不断变成规模更小的问题
规模小到一定程度可以直接得出它的解
求解
由最小规模问题的解得出较大规模问题的解
由较大规模问题的解不断得出规模更大问题的解
最后得出原来问题的解

递归的使用规则

(1)明确函数的功能
先不要去思考里面代码怎么写,首先搞清楚这个函数的干嘛用的,能完成什么功能

(2)明确原问题与子问题的关系
寻找 f(n) 与 f(n – 1) 的关系

(3) 明确递归基(边界条件)
递归的过程中,子问题的规模在不断减小,当小到一定程度时可以直接得出它的解
寻找递归基,相当于是思考：问题规模小到什么程度可以直接得出解？

算法 – 斐波那契数列

斐波那契数列：1、1、2、3、5、8、13、21、34 . . . 
F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3）
编写一个函数求第 n 项斐波那契数

根据递推式 T n    = T  n − 1    + T(n − 2) + O(1)，可得知时间复杂度：O(2n)
空间复杂度: O(n)
递归调用的空间复杂度 = 递归深度 * 每次调用所需的辅助空间

fib函数的调用过程

缺点: 出现了特别多的重复计算, 这是一种“自顶向下”的调用过程

斐波那契数优化1 – 记忆化

用数组存放计算过的结果，避免重复计算

时间复杂度: O(n)，空间复杂度: O(n)

斐波那契数优化2

去除递归调用

时间复杂度: O(n), 空间复杂度: O(n)

斐波那契数优化3

由于每次运算只需要用到数组中的 2 个元素，所以可以使用滚动数组来优化

时间复杂度: O(n)，空间复杂度: O(1)

斐波那契数优化4 – 位运算取代模运算

乘、除、模运算效率较低，建议用其他方式取代

斐波那契数优化5

时间复杂度: O(n), 空间复杂度: O(1)

算法 – 上楼梯（跳台阶）

问题

楼梯有 n 阶台阶，上楼可以一步上 1 阶，也可以一步上 2 阶，走完 n 阶台阶共有多少种不同的走法？

思路

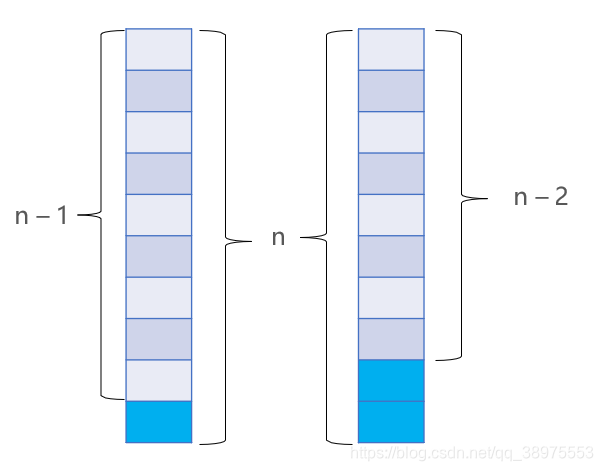
假设 n 阶台阶有 f(n) 种走法，第 1 步有 2 种走法
   (1) 如果上 1 阶，那就还剩 n – 1 阶，共 f(n – 1) 种走法
   (2) 如果上 2 阶，那就还剩 n – 2 阶，共 f(n – 2) 种走法
所以 f(n) = f(n – 1) + f(n – 2)

代码

跟斐波那契数列几乎一样，因此优化思路也是一致的

算法 – 汉诺塔（Hanoi）

问题

编程实现把 A 的 n 个盘子移动到 C(盘子编号是[1, n])
每次只能移动1个盘子
大盘子只能放在小盘子下面

情景1 – 1个盘子

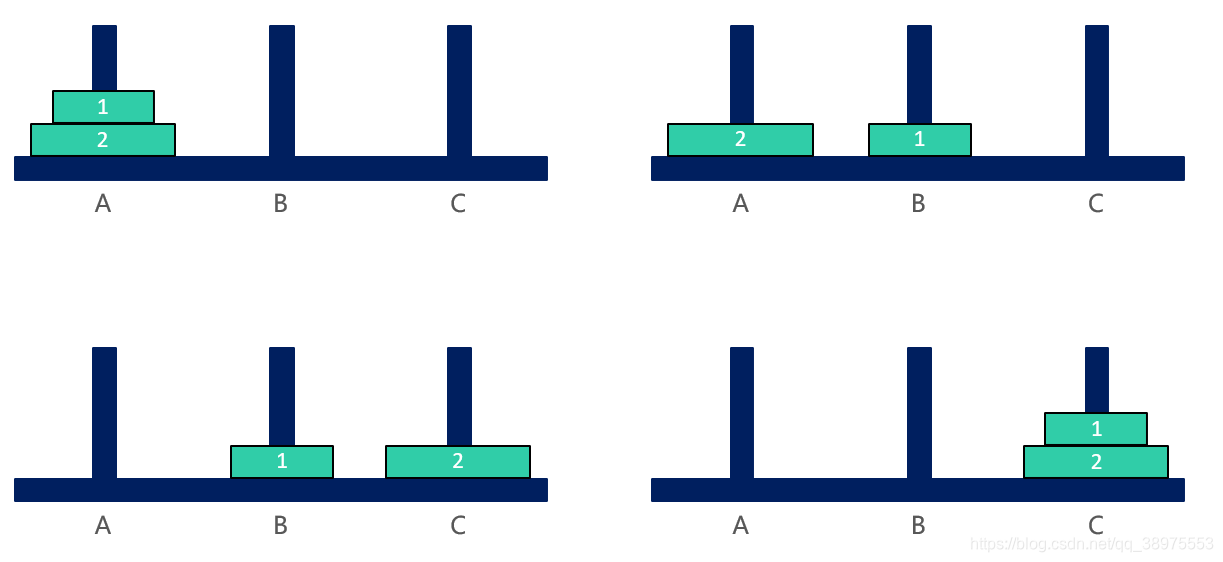
情景2 – 2个盘子

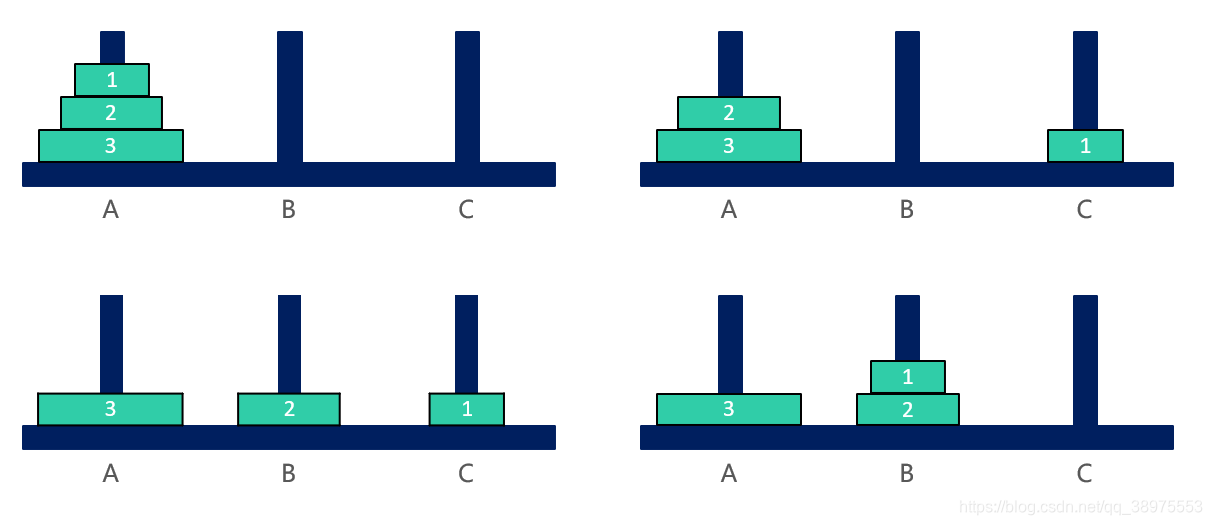
情景3 – 3个盘子

汉诺塔 – 递归思路

其实分 2 种情况讨论即可
1. 当 n == 1时，直接将盘子从 A 移动到 C
2. 当 n > 1时，可以拆分成3大步骤
      (1) 将 n – 1 个盘子从 A 移动到 B
      (2) 将编号为 n 的盘子从 A 移动到 C
      (3) 将 n – 1 个盘子从 B 移动到 C
步骤 (1) (2) 明显是个递归调用

汉诺塔 – 实现

T(n)= 2 ∗ T(n − 1) + O(1)
p因此时间复杂度是: O(2^n)
空间复杂度:O(n)

递归转非递归

递归调用的过程中, 会将每一次调用的参数、局部变量都保存在了对应的栈帧(Stack Frame)中

若递归调用深度较大，会占用比较多的栈空间，甚至会导致栈溢出
在有些时候，递归会存在大量的重复计算，性能非常差
这时可以考虑将递归转为非递归(递归100%可以转换成非递归)

递归转非递归方法

自己维护一个栈，来保存参数、局部变量
但是空间复杂度依然没有得到优化

在某些时候，也可以重复使用一组相同的变量来保存每个栈帧的内容

这里重复使用变量i保存原来栈帧中的参数
空间复杂度从 O(n)降到了 O(1)

尾调用（Tail Call）

尾调用：一个函数的最后一个动作是调用函数
如果最后一个动作是调用自身，称为尾递归（Tail Recursion），是尾调用的特殊情况

一些编译器能对尾调用进行优化，以达到节省栈空间的目的

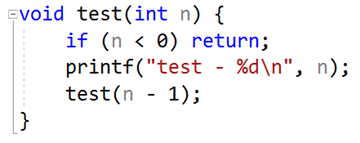
下面代码不是尾调用 

因为它最后1个动作是乘法

尾调用优化（Tail Call Optimization）

尾调用优化也叫做尾调用消除（Tail Call Elimination）
  1. 如果当前栈帧上的局部变量等内容都不需要用了，当前栈帧经过适当的改变后可以直接当作被尾调用的函数的栈帧 使用，然后程序可以 jump 到被尾调用的函数代码
  2. 生成栈帧改变代码与 jump 的过程称作尾调用消除或尾调用优化
  3. 尾调用优化让位于尾位置的函数调用跟 goto 语句性能一样高

消除尾递归里的尾调用比消除一般的尾调用容易很多
比如Java虚拟机(JVM) 会消除尾递归里的尾调用，但不会消除一般的尾调用(因为改变不了栈帧)
因此尾递归优化相对比较普遍，平时的递归代码可以考虑尽量使用尾递归的形式

 

尾调用优化前的汇编代码（C++）

尾调用优化后的汇编代码（C++）

 

尾递归示例

尾递归示例1 – 阶乘

求 n 的阶乘 1*2*3*...*(n-1)*n (n>0)

尾递归示例2 – 斐波那契数列