数据结构 树--笔记（一）

树

树的定义

树（Tree）是n(n>=0)个有限数据元素的集合。当n=0时，称这棵树为空树。在一刻非树T中：

• 有一个特殊的数据元素称为树的根节点，根节点没有前驱节点。
• 若n>1，除根节点之外的其余数据元素被分成m(m>0)个互不相交的集合T1,T2，……，Tm,其中每一个集合Ti(1≤i≤m)本身又是一棵树。树T1,T2，……，Tm称为这个根结点的子树。

二叉树基本概念

• 二叉树是个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不想交的、被分别称为左子树和右子树的二叉树组成。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点

二叉树的性质

• 性质1：一棵非空二叉树的第i层上最多有2^(i-1)个结点（i≤1）。

• 性质2：一棵深度为k的二叉树，最多具有2^(k-1)个结点。

• 性质3：对于一棵非空的二叉树，如果叶子结点树为n0，度数为2的节点数为n2，则有：
  n0 = n2+1

• 性质4：具有n个结点的完全二叉树的深度k为(log2n)+1

二叉树的存储结构

顺序存储结构

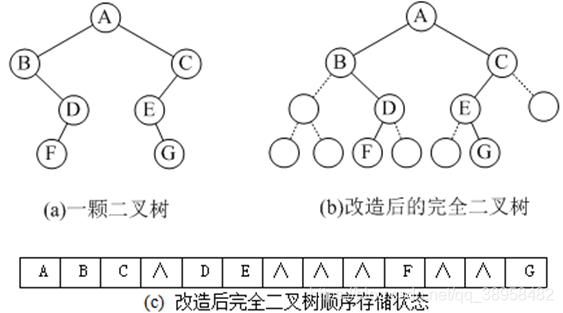
• 所谓二叉树的顺序存储，就是用一组连续的存储单元存放二叉树的结点。一般是按照二叉树结点从上至下、从左到右的顺序存储。
• 增添一些并不存在的空结点，使之成为一棵完全二叉树的形式，然后再用一维数组顺序存储。

链式存储结构

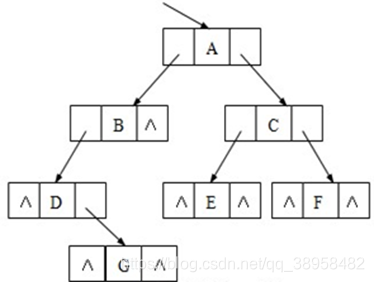
• 二叉链表存储
• 链表中每个结点由三个域组成，除了数据域外，还有两个指针域，分别用来给出该站点左孩子和右孩子所在的链结点的存储地址。

二叉树的遍历

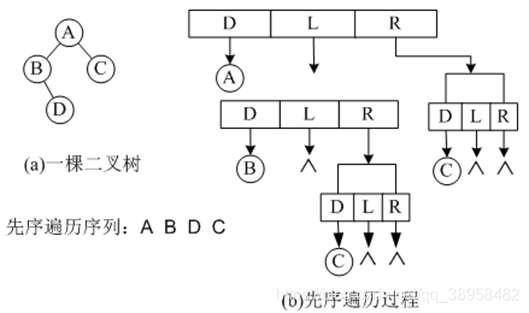
先序遍历

• 先序遍历的递归过程为：若二叉树为空，遍历结束。否则，
  • 访问根节点；
  • 先序遍历根节点的左子树；
  • 先序遍历根结点的右子树；

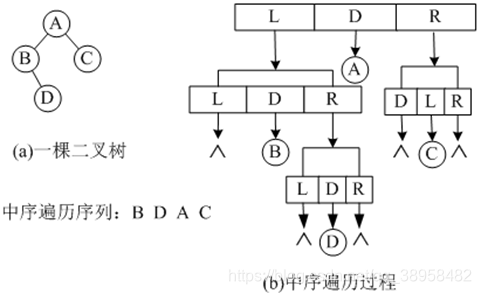
中序遍历

• 中序遍历的递归过程：若二叉树为空，遍历结束。否则
  • （1）中序遍历根结点的左子树；
  • （2）访问根结点；
  • （3）中序遍历根结点的右子树；
    

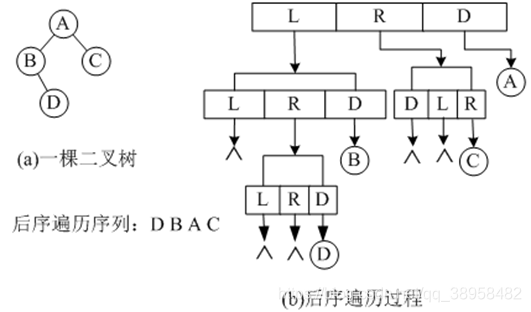
后序遍历

• 后序遍历的递归过程为：若二叉树为空，遍历结束，否则
• （1）后序遍历根结点的左子树；
• （2）后序遍历很结点的右子树；
• （3）访问根节点；