迪克斯特拉算法(最短路径)理解及代码实现(java)

介绍
迪克斯特拉算法是基于有向图（无负权）有负权边的图结构不适用这种算法,因为有负权边会导致这种算法不管用
如图: 求a1定点到其他定点的最短距离

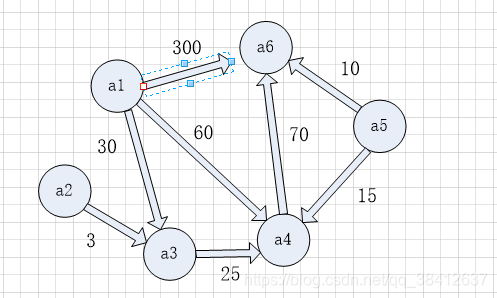
对于每一个结点 都遵循运算法则:
找出最便宜节点，（从a1结点出发，到其邻居最小开销的结点）。
更新该节点邻居的开销。
重复这个过程,直到对每个结点都这样做了。
计算最终路径
a，初始化 distance 数组，初始化时，我们对能直接到达的节点附上权值，不能直接到达的节点，我们暂且设为无穷大。
得到以下结果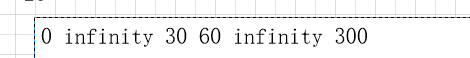
建立集合temp,表示已经确定为最短路径的顶点.我们认为a1->a1 = 0 所以初始化为{a1} ;
b，找出distance数组中最小的值（但不包括集合temp中的顶点），这里最小值为 30，所以a1→a3的最短路径就是30 ，于是我们将a3加入到集合temp中，temp就变为{a1，a3}
c, 随着a3加入集合T中，数组distance会怎么变化呢？a3→a4为25，那么a1→a4可以通过a3中转a1→a3→a4=30+25=55，因为55 < distance[3]，所以distance[3]=55，所以:

重复b,c 两步 直到所有定点全部加入temp集合中
public class MinDistance {

public static void main(String[] args) {
    //这里我们将无穷大定义为int类型最大值 2^32-1  2147483647
    int infinity =  Integer.MAX_VALUE;
    //构建地图
    int[][] paraGraph=new int[][]{
            //从a1定点出发，到各定点的开销 从a1开始
            {0,       infinity,30,60,      infinity,    300},
            //从a2顶点出发,到各个顶点的开销 从a1开始
            {infinity,      0,  3,infinity,infinity,infinity},
            //从a3顶点出发,到各个顶点的开销 从a1开始
            {infinity,infinity, 0,      25,infinity,infinity},
            //从a4顶点出发,到各个顶点的开销 从a1开始
            {infinity,infinity,infinity, 0,infinity,70},
            //从a5顶点出发,到各个顶点的开销 从a1开始
            {infinity,infinity,infinity, 15,      0,10},
            //从a6顶点出发,到各个顶点的开销 从a1开始
            {infinity,infinity,infinity,infinity,infinity,0}
    };
    int[] distance=new int[6];//开销集合
    boolean[] temp=new boolean[6];//temp集合
    temp[0]=true;

    for(int i=0;i<6;i++)
        distance[i]=paraGraph[0][i];

    minDistance(paraGraph, distance, temp);
    for(int i=0;i<distance.length;i++)
        System.out.print(distance[i]+" ");
}
public static void  minDistance(int[][] paraGraph,int[] distance,boolean[] temp){
    while(true){//外层循环
        int min=Integer.MAX_VALUE;
        int index=-1;

        //内层循环每次找出temp中最小值
        for(int i=0;i<distance.length;i++){
            //6个长度
            if(temp[i] == true)
                continue;//不包括集合temp中的顶点 已经包括了就继续循环,不在加入范围
            else{
                //i =5 时 300 <30 不满足 跳出内存循环
                if(distance[i]<min){
                    index=i;
                    min=distance[i];
                }
            }
        }

        if(index==-1) break;//直到所有顶点全部加入集合中

        temp[index]=true;//visited[2] = true; ==> 10 min = 10 visited[4] = 30; min = 30  min = 100,visited[5] = 100
        //第一次 index = 2,
        for(int i=0;i<paraGraph.length;i++){
            //如果a3结点
            if(paraGraph[index][i]!=Integer.MAX_VALUE){
                if(distance[i] < min+paraGraph[index][i]){//30+0
                    distance[i] = distance[i];
                }else{
                    distance[i]  =  min + paraGraph[index][i]; //index =2  i =5
                }
            }
        }
    }
}

}
执行结果如下:

参考资料 算法图解
参考连接:https://blog.youkuaiyun.com/weixin_40423553/article/details/79613820