cordic算法的FPGA实现

李逍遥lzx

已于 2025-03-06 10:53:46 修改

阅读量1k

点赞数 5

分类专栏： FPGA 文章标签：算法

于 2025-03-05 15:54:44 首次发布

本文链接：https://blog.youkuaiyun.com/qq_38360574/article/details/145580366

版权

FPGA 专栏收录该内容

5 篇文章

订阅专栏

CORDIC（Coordinate Rotation Digital Computer）算法是一种用于计算三角函数、双曲函数和其他数学函数的迭代算法。它通过简单的移位和加法操作来实现复杂的数学计算，非常适合在FPGA中实现。本文将简要介绍CORDIC算法的原理，以及如何从CORDIC统一的方程式中得到计算sin、cos，反正切，开方，向量模长和相角，

1.CORDIC算法的原理

向量OA与单位圆的交点为 A(xa,ya) , 与正半轴的夹角记为α, xa,ya与α的关系为。

$x_a = cos\alpha$

$y_a = sin\alpha$

将向量OA逆时针旋转β角得到向量OB，欲求向量OB的坐标有

$x_B = cos(\alpha +\beta)=cos\alpha cos\beta - sin\alpha sin\beta$

$y_B = sin(\alpha +\beta) = sin\alpha cos\beta + cos\alpha sin\beta$

有

$x_B =x_a cos\beta - y_a sin\beta$

$y_B = y_a cos\beta + x_a sin\beta$

提取cosβ，有

$x_B = cos\beta(x_a - y_a tan\beta)$

$y_B = cos\beta (y_a+ x_a tan\beta)$

当旋转角度满足条件1

$tan\beta = 2^{-n}$

有

$x_B = cos\beta(x_a - y_a 2^{-n})$

$y_B = cos\beta (y_a+ x_a 2^{-n})$

向量的旋转进一步转化为转换为移位，相加和相乘。当我们用一系列的满足条件1的角度累加逼近我们输入的角度时候，我们所得到坐标值便逼近输入角度对应的正弦和余弦。满足条件1的角度及对应的正弦值为常数，因此可以将这些值固定在代码中以供算法实现。当我们将向量由相角零旋转至指定相角时，将根据旋转后的角度与指定的角度之间的大小关系确定旋转方向。当我们反过来将向量由指定相角旋转至相角零的时候，则讨论角度的正负。

又因为

$\sum tan^{-1}2^{-n}\approx 99.8829$

$-\sum tan^{-1}2^{-n}\approx -99.8829$

因此满足条件1的角度的持续叠加并不能覆盖整个圆周，因此在使用cordic算法对角度进行逼近的时候，需要将角度偏转到能够表示的范围内。记处理至收敛后得到的坐标为(x0,yo), 假设角度范围为0~360，不同角度范围所做的处理及最终的坐标如下:

输入角度范围	处理方式	最终的坐标
[0,90]	无	(x0, yo)
[90,180]	-90	(-yo, x0)
[180,270]	-270	(y0, -x0)
[270,360]	-360	（x0, yo）

2.CORDIC算法的matlab仿真

本小节先对cordic算法进行双精度数的仿真，当旋转角度与输入角度相等的时候，停止迭代

2.1 matlab双精度数仿真

xa = 1;
ya = 0;
theta = 70;

mini_theta = zeros(1024,1);
sin_70= sin(70/180*pi);
cos_70 = cos(70/180*pi);

%正切值为2^-n对应的角度
for i = 1:length(mini_theta)
    mini_theta(i) = atan(2^(-(i-1)))/pi*180;
end

%正切值为2^-n对应的角度的余弦值
cos_mini_theta = zeros(1024,1);
for i = 1:length(mini_theta)
    cos_mini_theta(i) = cos(mini_theta(i)/180*pi);
end
flag = 1; %方向判定
n = 0;
buffer = zeros(1024,7); %中间计算结果寄存
while(n<=1023)
        n=n+1;
         buffer(n,1)=theta;
         buffer(n,2)=xa;
         buffer(n,3)=ya;

         cos_theta = cos(theta/180*pi);
         buffer(n,4)=cos_theta;

         sin_theta = sin(theta/180*pi);
         buffer(n,5)=sin_theta;
         
         buffer(n,6) =flag;
         buffer(n,7) = cos_mini_theta(n);
       
        
    %旋转方向判断
    if(theta>0)
        theta = theta - mini_theta(n);
        flag = 1;
    else 
        theta = theta + mini_theta(n);
        flag = -1;
    end
    %坐标计算
        xa_buffer = cos_mini_theta(n)*(xa - flag* ya*2^(-(n-1)));
        ya_buffer = cos_mini_theta(n)*(ya + flag*xa*2^(-(n-1)));
 
        xa = xa_buffer;
        ya = ya_buffer;
        dealt_sin =  sin_70 - ya; 
        dealt_cos =  cos_70 - xa; 
          buffer(n,8) = dealt_sin;
         buffer(n,9) = dealt_cos;
end

上图显示了角度、正弦值、余弦值在迭代过程中的变化，可以看出当迭代次数到达16的时候，角度、正弦值、余弦值都很接近理论值。当迭代次数固定的时候，可以将cordic 迭代方程中的cos项提取出来，省去与cos相乘的步骤

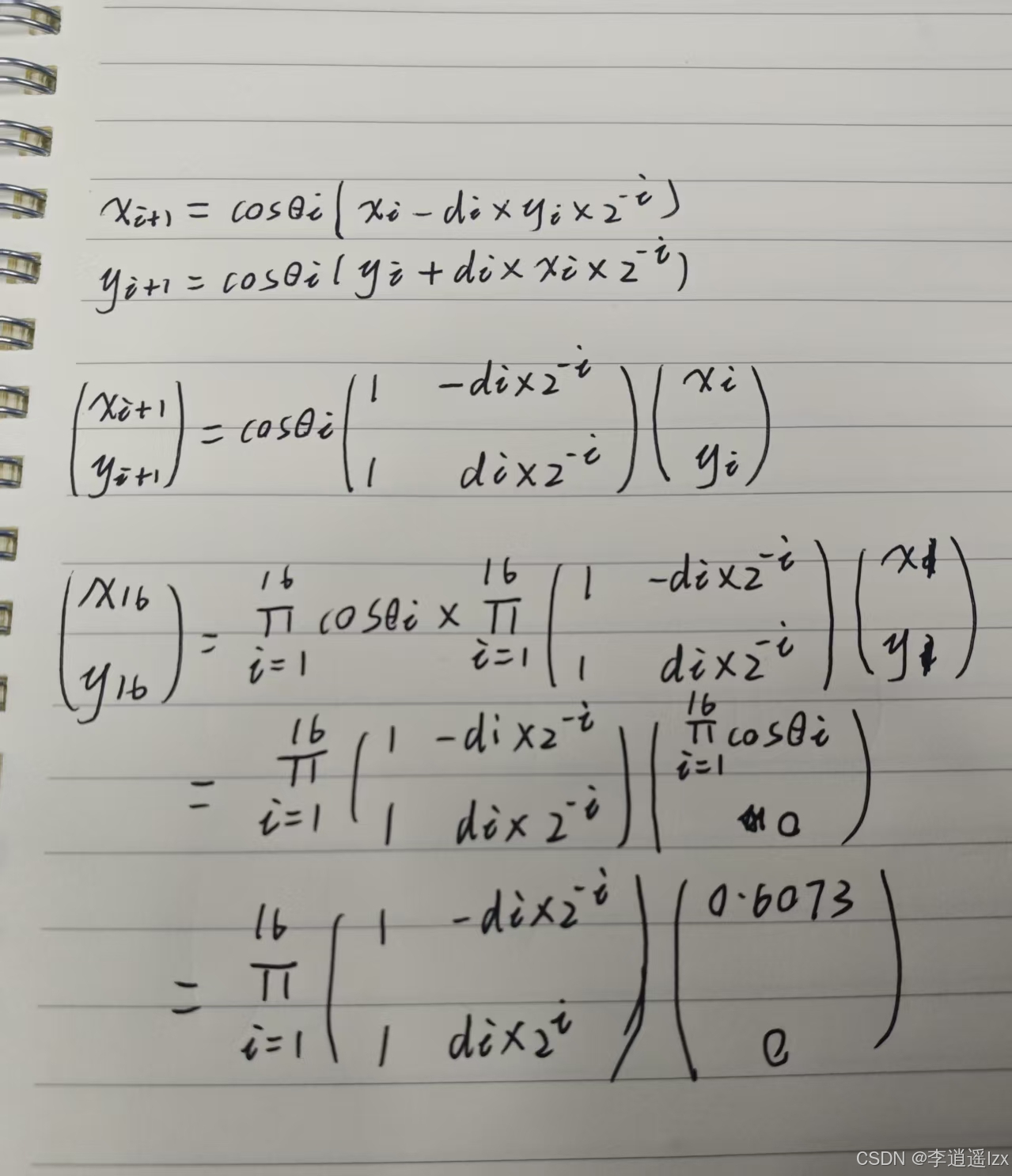
function [sin_o,cos_o] = cordic_cal(deg,num_of_iterration)
%UNTITLED2 此处提供此函数的摘要
%   此处提供详细说明
flag_cordinate = 0;
if deg > 90 && deg <=180
   deg = deg - 90;
   flag_cordinate = 1;
elseif deg >180 && deg <= 270
    deg = deg -270;
    flag_cordinate = 2;
elseif deg >270 && deg <= 360
    deg = deg -360;
    flag_cordinate = 3;
end

theta = zeros(num_of_iterration,1);
cos_theta =zeros(num_of_iterration,1);
for i = 1 :length(theta)
    theta(i) = atan(2^(-(i-1)));
    cos_theta(i) = cos(theta(i));
end
theta =theta/pi*180;
theta_initial = deg;
 xa = 0.6073;
 ya = 0;
buffer = zeros(1024,5);

 n=1;
 flag = 0;

while(n<num_of_iterration)
    if theta_initial > 0
        theta_initial = theta_initial - theta(n);
        flag =1;
    
    else
        theta_initial = theta_initial + theta(n);
        flag = -1;
    end

    xb = (xa -flag* ya/2^(n-1));
    yb = (ya + flag*xa/2^(n-1));
    xa = xb;
    ya = yb;
    n=n+1;
end

if flag_cordinate == 1
    sin_o = xa;
    cos_o = -ya;
elseif flag_cordinate == 2
    sin_o = -xa;
    cos_o = ya;
elseif flag_cordinate == 3
    sin_o = ya;
    cos_o = xa;
else 
    sin_o = ya;
    cos_o = xa;
end

测试


numn_of_iterration = 16;
theta = 0:1:360;
num_of_theta =7;
num_of_cos = 16;
num_of_cordinate  = 16;
sin_o = zeros(length(theta),1);
cos_o = zeros(length(theta),1);
sin_standard = zeros(length(theta),1);
cos_standard = zeros(length(theta),1);
dealt_sin_ = zeros(length(theta),1);
dealt_cos = zeros(length(theta),1);

for i = 1 : length(theta)
     sin_standard(i) = sin(theta(i)/180*pi); 
     cos_standard(i) = cos(theta(i)/180*pi); 
    theta(i) = floor(theta(i)*2^num_of_theta);
     [sin_o(i),cos_o(i)] = cordic_cal_fixed_point(theta(i),numn_of_iterration,num_of_theta,num_of_cos,num_of_cordinate);
    
     dealt_sin(i) = sin_standard(i) - sin_o(i)/2^num_of_cordinate; 
     dealt_cos(i) = cos_standard(i)-  cos_o(i)/2^num_of_cordinate; 

end


 subplot(121);
 plot(sin_o/2^num_of_cordinate,'r','LineWidth',0.5);
 hold on
 plot(cos_o/2^num_of_cordinate,'b','LineWidth',0.5);
 xlabel('theta');
 ylabel('amplitude');
 legend('sin','cos');
 grid on;
 subplot(122)
 plot(dealt_sin,'r','LineWidth',0.5);
 hold on
 plot(dealt_cos,'b','LineWidth',0.5);
 xlabel('theta');
 ylabel('amplitude');
 legend('dealt\_sin','dealt\_cos');
 grid on;

结果

2.2 matlab定点化仿真

function [sin_o,cos_o,buffer] = cordic_cal_fixed_point(deg,num_of_iterration,num_of_theta,num_of_cos,num_of_cordinate)
%UNTITLED2 此处提供此函数的摘要
%   此处提供详细说明

%角度坐标确定及处理
flag_cordinate = 0;
if deg > 90*2^num_of_theta && deg <=180*2^num_of_theta
   deg = deg - 90*2^num_of_theta;
   flag_cordinate = 1;
elseif deg >= 180*2^num_of_theta && deg < 270*2^num_of_theta
    deg = deg - 270 *2^num_of_theta;
    flag_cordinate = 2;
elseif deg >=270*2^num_of_theta
    deg = deg - 360 *2^num_of_theta;
    flag_cordinate = 3;
end

theta = zeros(num_of_iterration,1);
cos_theta =zeros(num_of_iterration,1);

%余弦
for i = 1 :length(theta)
    theta(i) = atan(2^(-(i-1)));
    cos_theta(i) = floor(cos(theta(i))*2^num_of_cos);
end

%初始化
theta =floor(theta/pi*180*2^num_of_theta);
theta_initial = deg;
 xa =floor(0.6073*2^num_of_cordinate);
 ya = 0;
buffer = zeros(1024,8);
 n=1;
 flag = 0;
theta1 = theta_initial/2^num_of_theta;

while(n<num_of_iterration)
    buffer(n,1) = xa ;
    buffer(n,2) = ya ; 
    buffer(n,3) = theta_initial ;
    buffer(n,4) = flag;
    if  theta_initial< 0
        theta_initial = theta_initial + theta(n);
        flag =-1;
    else
        theta_initial = theta_initial - theta(n);
        flag = 1;
    end
    xb = (xa -flag* ya/2^(n-1));
    y_shift = ya/2^(n-1);
    yb = (ya + flag*xa/2^(n-1));
    x_shift = xa/2^(n-1);
    buffer(n,5) = theta(n);
    buffer(n,6) = y_shift;
    buffer(n,7) = x_shift;
    xa = xb;
    ya = yb;
    n=n+1;
    buffer(n,8) = n;
end
if flag_cordinate == 0
    sin_o = ya;
    cos_o = xa;
elseif flag_cordinate == 1
    sin_o = xa;
    cos_o = -ya;
elseif flag_cordinate == 2
    sin_o = -xa;
    cos_o = ya;
elseif flag_cordinate ==3
    sin_o = ya;
    cos_o = xa;
end

测试代码


numn_of_iterration = 16;
theta = 0:1:360;
num_of_theta =7;
num_of_cos = 16;
num_of_cordinate  = 16;
sin_o = zeros(length(theta),1);
cos_o = zeros(length(theta),1);
for i = 1 : length(theta)
    theta(i) = floor(theta(i)*2^num_of_theta);
     [sin_o(i),cos_o(i)] = cordic_cal_fixed_point(theta(i),numn_of_iterration,num_of_theta,num_of_cos,num_of_cordinate)
end
plot(sin_o,'r','LineWidth',2);
hold on
plot(cos_o,'b','LineWidth',2);
xlabel('theta');
ylabel('amplitude');
legend('sin','cos');
grid on;

仿真结果

3.CORDIC算法的verilog实现

`timescale 1ns / 1ps
module cordic(
        input                       sys_clk     ,    
        input                       rst         ,
        input                       i_theta_vld ,
        input        [15:0]         i_theta     ,
        output reg signed [17:0]    o_sin       ,
        output reg signed [17:0]    o_cos       ,
        output reg                  cordic_tvld
);
//theta_in、cos、坐标小数部分位宽分别为7、16、16, 迭代次数为12
reg [17:0] cos_theta    [11:0];
reg [15:0] theta        [11:0];

//象限判定
reg [1:0] quadrant; //象限

//cordic 迭代
reg signed [15:0]   theta_rotate ; 
reg                 cal_en;
reg         [3:0]   cnt_iteration;     //迭代次数
reg signed [17:0]   cos_shift;
reg signed [17:0]   sin_shift;
reg signed [17:0]   sin;
reg signed [17:0]   cos;

//输出有效标志
reg cal_en_r1;
wire  neg_cal_en;

//固定系数准备

    always@(posedge sys_clk)begin
        if(rst)
            cos_theta[0]  <= 46340;    
            cos_theta[1]  <= 58617;    
            cos_theta[2]  <= 63579;    
            cos_theta[3]  <= 65029;    
            cos_theta[4]  <= 65408;    
            cos_theta[5]  <= 65504;    
            cos_theta[6]  <= 65528;    
            cos_theta[7]  <= 65534;    
            cos_theta[8]  <= 65535;    
            cos_theta[9]  <= 65535;    
            cos_theta[10] <= 65535;    
            cos_theta[11] <= 65535;    
            cos_theta[12] <= 65535;     
    end

    always@(posedge sys_clk)begin
        if(rst)
            theta[0 ]  <= 5760;    
            theta[1 ]  <= 3400;    
            theta[2 ]  <= 1796;    
            theta[3 ]  <= 912;    
            theta[4 ]  <= 457;    
            theta[5 ]  <= 229;    
            theta[6 ]  <= 114;    
            theta[7 ]  <= 57;    
            theta[8 ]  <= 28;    
            theta[9 ]  <= 14;    
            theta[10]  <= 7;    
            theta[11]  <= 3;    
    end


//角度象限判定

    always@(posedge sys_clk)begin
        if(rst)
            quadrant <= 'd0;
        else if(i_theta_vld)begin
            if(i_theta > 11520 && i_theta <=23040 )
                quadrant <= 'd1;
            else if( i_theta > 23040 && i_theta <= 34560)
                quadrant <= 'd2;
            else if( i_theta > 34560 )
                quadrant <= 'd3;
            else 
                quadrant <= 'd0;
        end
    end

//-------------------
//cordic 迭代

    always@(posedge sys_clk)begin
        if(rst)
            cnt_iteration <= 'd0;
        else if(cal_en)
            cnt_iteration <= cnt_iteration + 'd1;
        else 
            cnt_iteration <= 'd0;
    end

    always@(posedge sys_clk)begin
        if(rst)
            cal_en <= 'd0; 
        else if(i_theta_vld)
            cal_en <= 'd1;
        else if(cnt_iteration == 'd15)
            cal_en <= 'd0;
    end

//角度旋转

    always@(posedge sys_clk)begin
        if(rst)
            theta_rotate <= 'sd0;
        else if(i_theta_vld)begin
            if(i_theta > 11520 && i_theta <=23040 )
                theta_rotate <= i_theta - 11520;
            else if( i_theta > 23040 && i_theta <= 34560 )
                theta_rotate <= i_theta - 34560;
            else if(i_theta > 34560)
                theta_rotate <= i_theta - 46080;
            else 
                theta_rotate <= i_theta;
        end
        else if(cal_en)begin
            if(theta_rotate[15])begin
                theta_rotate <= theta_rotate + theta[cnt_iteration];    
            end
            else begin
                theta_rotate <= theta_rotate - theta[cnt_iteration];   
            end
        end
        else 
            theta_rotate <= theta_rotate;
    end

//三角函数计算

    always@(posedge sys_clk)begin
        if(rst)begin
            sin <= 'sd0;
            cos <= 'sd0;
        end
        else if(i_theta_vld)begin
            sin <= 'sd0; 
            cos <= 'sd39800;       
        end 
        else if(cal_en)begin
            if(theta_rotate[15])begin
                sin <= sin - cos_shift ;
                cos <= cos + sin_shift;
            end
            else begin
                sin <= sin + cos_shift ;
                cos <= cos - sin_shift;
            end
        end
    end    


    always@(*)begin
        case(cnt_iteration)
            0   :   cos_shift <= cos;
            1   :   cos_shift <= cos >>> 1 ;
            2   :   cos_shift <= cos >>> 2 ;
            3   :   cos_shift <= cos >>> 3 ;
            4   :   cos_shift <= cos >>> 4 ;
            5   :   cos_shift <= cos >>> 5 ;
            6   :   cos_shift <= cos >>> 6 ;
            7   :   cos_shift <= cos >>> 7 ;
            8   :   cos_shift <= cos >>> 8 ;
            9   :   cos_shift <= cos >>> 9 ;
            10  :   cos_shift <= cos >>> 10;
            11  :   cos_shift <= cos >>> 11;
            12  :   cos_shift <= cos >>> 12;
            13  :   cos_shift <= cos >>> 13;
            14  :   cos_shift <= cos >>> 14;
            15  :   cos_shift <= cos >>> 15;
        default : cos_shift <= cos;
        endcase
    end
    always@(*)begin
        case(cnt_iteration)
            0   :   sin_shift <= sin      ;
            1   :   sin_shift <= sin >>> 1 ;
            2   :   sin_shift <= sin >>> 2 ;
            3   :   sin_shift <= sin >>> 3 ;
            4   :   sin_shift <= sin >>> 4 ;
            5   :   sin_shift <= sin >>> 5 ;
            6   :   sin_shift <= sin >>> 6 ;
            7   :   sin_shift <= sin >>> 7 ;
            8   :   sin_shift <= sin >>> 8 ;
            9   :   sin_shift <= sin >>> 9 ;
            10  :   sin_shift <= sin >>> 10;
            11  :   sin_shift <= sin >>> 11;
            12  :   sin_shift <= sin >>> 12;
            13  :   sin_shift <= sin >>> 13;
            14  :   sin_shift <= sin >>> 14;
            15  :   sin_shift <= sin >>> 15;
        default : sin_shift <= sin;
        endcase
    end

//output

    always@(posedge sys_clk)begin
        cal_en_r1 <= cal_en;
    end
    
    
    always@(posedge sys_clk)begin
        if(rst)begin
            o_sin <= 'sd0;
            o_cos <= 'sd0; 
        end 
        else if(neg_cal_en)begin
           case(quadrant)
                0 : begin
                    o_sin <= sin;
                    o_cos <= cos;
                end
                1 : begin
                    o_sin <= cos;
                    o_cos <= -sin;        
                end
                2 : begin
                    o_sin <= -cos;
                    o_cos <= sin;    
                end
                3 : begin
                    o_sin <= sin;
                    o_cos <= cos;    
                end 
            default : begin
               o_sin <= 'sd0;
               o_cos <= 'sd0;            
            end
            endcase
        end
    end
    
    always@(posedge sys_clk)begin
        cordic_tvld <= neg_cal_en;
    end
    assign neg_cal_en = cal_en_r1 & ~cal_en;

endmodule

仿真

module tb_cordic(

    );
    reg   sys_clk;
    reg   rst;
    wire    i_theta_vld;
    wire    [15:0]  i_theta;
    reg   [8:0]     theta;
    // cordic Outputs
    wire  [17:0]  o_sin;
    wire  [17:0]  o_cos;
    wire  cordic_tvld;
    initial begin
        sys_clk = 0;
        rst = 1;
        #100
        rst = 0;
    end
    reg [7:0] cnt ;
    always@(posedge sys_clk)begin
        if(rst)
            cnt <= 'd0;
        else 
            cnt <= cnt + 'd1;   
    end
    assign i_theta_vld = cnt == 8'hff;
    always@(posedge sys_clk)begin
        if(rst)
            theta <= 'd0;
        else if(i_theta_vld)begin
            if(theta == 360)
                theta <= 'd0;
            else 
                theta <= theta + 'd1; 
        end
    end
    assign i_theta = theta*128;
    always #10 sys_clk = ~sys_clk;
    cordic  u_cordic (
        .sys_clk                 ( sys_clk       ),
        .rst                     ( rst           ),
        .i_theta_vld             ( i_theta_vld   ),
        .i_theta                 ( i_theta       ),
    
        .o_sin                   ( o_sin         ),
        .o_cos                   ( o_cos         ),
        .cordic_tvld             ( cordic_tvld   )
    );

仿真结果