KNN

KNN

---

如何衡量相似（距离）

不同属性之间的比较

• 标称属性
  • 属性值匹配
  • 属性值不匹配
  • $0-1$ 函数
• 序数属性
  • 可以考虑量化序数属性
  • $d=\frac{|p-q|}{n-1}$
• 区间或者比率属性
  • 属性值差的绝对值
  • 属性值比率
  • $d=|p-q|$
  • $s=-d,s=\frac{1}{1+d},s=1-\frac{d-\min d}{\max d-\min d}$

距离

距离公理，度量

• 非负性 $d(a,b)\ge 0$
• 到自身的距离为0 $d(a,a)=d(b,b)=0$
• 对称性 $d(a,b)=d(b,a)$
• 三角不等式 $d(a,b)\le d(a,k)+d(b,k)$

欧氏距离 $(EuclideanDistance)$

$$x_a=(x_{a1},...,x_{an}),x_b=(x_{b1},...,x_{bn})$$

$$\Rightarrow d(a,b)=\sqrt{(x_{a1}-x_{b1}{)}^2+...+(x_{an}-x_{bn}{)}^2}$$

曼哈顿距离 $(ManhattanDistance)$

$$d(a,b)=|x_{a1}-x_{b1}|+...+|x_{an}-x_{bn}|$$

闵可夫斯基距离 $(MinkowskiDistance)$

• 普通的闵可夫斯基距离
  $$d(a,b)=(|x_{a1}-x_{b1}{|}^p+...+|x_{an}-x_{bn}{|}^p{)}^{\frac{1}{p}}$$
  其中 $p$ 为一个整数
• 加权闵可夫斯基距离
  $$d(a,b)=(w_1|x_{a1}-x_{b1}{|}^p+...+w_n|x_{an}-x_{bn}{|}^p{)}^{\frac{1}{p}}$$
  其中 $p$ 为一个整数

可以发现，欧氏距离以及曼哈顿距离都是闵可夫斯基距离的一个特例

马氏距离 $(MahalanobisDistance)$

$$d(a,b)=(a-b){\Sigma }^{-1}(a-b{)}^T$$
其中 $\Sigma$ 是数据的协方差矩阵
$${\Sigma }_{j,k}=\frac{1}{n-1}\sum _{i=1}^n(X_{ij}-{\bar{X}}_j)(X_{ik}-{\bar{X}}_k)$$

相当于引入了对方向上的方差进行惩罚的机制。

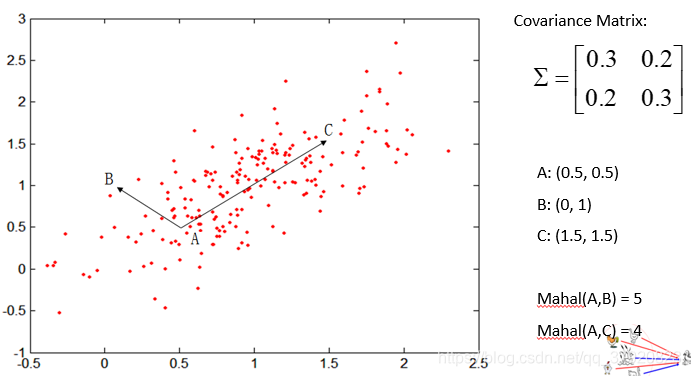
一些不满足距离或度量的评估标准

• 集合
  • $d(A,B)=size(A-B)$
  • $d(A,B)=size(A-B)+size(B-A)$
• 时间
  • $d(t_1,t_2) = \begin{Bmatrix}
    t_2-t_1 & 如果 t_1 \leq t_2 \
    24+(t_2 - t_1) & 如果t_1 \geq t_2
    \end{Bmatrix} $
• 简单匹配系数 $(SimpleMatchingCoefficent)$
  • SMC = $\frac{numberofmatches}{numberofattributes}=\frac{M_{11}+M_{00}}{M_{11}+M_{00}+M_{10}+M_{01}}$
• $JaccardCoefficent$
  • $J=\frac{M_{11}}{M_{11}+M_{00}+M_{10}+M_{01}}$

余弦相似度

$$d(a,b)=\frac{a\cdot b}{||a||\ast ||b||}$$

不同属性的距离综合评估

• 对于不同属性通常会用不同的距离标准去衡量。
• 不同属性的重要性也可能不同
• 可以采取不同属性的距离进行加权求和的形式来解决这个问题

---

$KNN$

简单介绍

• 将个类训练样本划分为若干子类
• 在每一个子类中确定代表点
  • 常见使用质心或者质心周围的点作为代表点
• 计算未知样本与这些代表点的距离，最近的作为决策结果
• 由于决策受代表点的影响很大，所以有可能导致错误率升高

代表点的选取

• 增加代表点的数量会使分类器效果增加吗？
• 将所有样本作为代表点。新样本与哪 $k$ 个代表点最相似就基于投票多数类别决策。
  • $y^{\prime }=arg\underset{y}{\max }{\sum }_{(x_i,y_i)\in D_k}I(v=y_i)$
• 通过对每一个最近邻的距离进行加权
  • $y^{\prime }=arg\underset{y}{\max }{\sum }_{(x_i,y_i)\in D_k}{w}_i\ast I(v=y_i)$
  • $w_i=\frac{1}{d(x^{\prime },x_i{)}^2}$

对于 $k$ 值大小的讨论

• $k$ 值太小，则模型对噪声敏感程度大
• $k$ 值太大，则可能误分类样例
• 使用交叉验证法选取最优 $k$ 值

尺度变换非常重要

$KD$ 树

• 对 $k$ 维空间中的实例点进行存储以便于进行快速检索的树形数据结构
• 二叉树
• 是对 $k$ 维空间的一种划分，划分边界垂直于坐标轴。
• 每一个节点对应于一个矩形区域
• 如果使用中位数作为切分点，那么得到的 $kd$ 树是平衡的
  • 平衡的 $kd$ 树效率未必是最优的

构造过程

• 构造根节点，选择 $x_1$ 为坐标轴，以样本在这个维度上的中位数进行划分，切分方向垂直于坐标轴。在根节点处保存对应的实例
• 对于深度为 $j$ 的节点，选择 $x_l,l=j(modk)+1$ 作为坐标轴，以该节点中的样本在维度上的中位数进行划分；在节点处保存实例。重复直至划分后的区域没有样本。

搜索过程

• 首先找到包含目标点的叶结点作为当前最近点：兄根节点出发，递归向下访问，每一次访问比较对应维度的大小，进入左节点或者右节点。
• 从叶节点出发回退
  • 如果当前节点保存的样本距离比当前最近点的距离还小，则更新当前最近点。
  • 当前最近点一定存在于该节点的某个子节点的区域，所以检查该节点的父节点的另一子节点的区域中是否有更近的点
  • 如果有，则移动到另一个节点。递归进行搜索
  • 如果没有，向上回退，递归搜索。
• 回退至根节点时，搜索结束。返回当前最近点。

当维数较大时， $kd$ 树的搜索效率降低，只有当 $N$ 远大于 $2^D$ 时，效率优势明显。