本文介绍了决策树的基础知识，包括如何划分属性，如Entropy、GiniIndex和MisclassificationError等度量标准，以及ID3、C4.5和CART算法的工作原理。C4.5是对ID3的改进，解决了信息增益偏向多值特征的问题，CART则采用Gini Index进行二元划分。此外，文章还探讨了树的剪枝方法，如错误率降低修剪和预剪枝、后剪枝策略，以防止过拟合。
决策树
如何划分属性
一些度量
- 选择最优分裂的度量是根据划分后子女节点的不纯性的程度
- 不纯度越低，类分布就越倾斜
- 度量不纯度的方法
- E n t r o p y Entropy Entropy
- G i n i I n d e x Gini Index GiniIndex
- M i s c l a s s i f i c a t i o n E r r o r Misclassification Error MisclassificationError
E n t r o p y Entropy Entropy:
E
n
t
r
o
p
y
(
t
)
=
−
∑
j
p
(
j
∣
t
)
log
2
p
(
j
∣
t
)
Entropy(t) = -\sum_jp(j|t)\log_2p(j|t)
Entropy(t)=−j∑p(j∣t)log2p(j∣t)其中
p
(
j
∣
t
)
p(j|t)
p(j∣t) 是给定节点
t
t
t 中类
j
j
j 所占的比例
是节点的一种纯度的度量方式
- 当时均匀分布时，取得最大值 log 2 n c \log_2n_c log2nc
- 当只有一个类别时，取得最小值 0 0 0
G i n i I n d e x Gini Index GiniIndex:
G I N I ( t ) = 1 − ∑ j [ p ( j ∣ t ) ] 2 GINI(t) = 1-\sum_j[p(j|t)]^2 GINI(t)=1−j∑[p(j∣t)]2
- 最大值为 1 − 1 n c 1-\frac{1}{n_c} 1−nc1,对应为均匀分布
- 最小为 0 0 0，对应为只有一个类别
M i s c l a s s i f i c a t i o n E r r o r Misclassification\ Error Misclassification Error:
E r r o r ( t ) = 1 − max i p ( i ∣ t ) Error(t) = 1-\max_ip(i|t) Error(t)=1−imaxp(i∣t)
- 最大值为 1 − 1 n c 1-\frac{1}{n_c} 1−nc1,对应为均匀分布
- 最小为 0 0 0，对应为只有一个类别
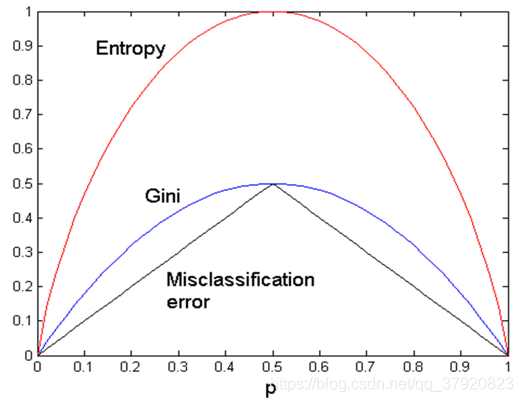
二分类时的三种度量比较:
划分
Δ = I ( p a r e n t ) − ∑ j = 1 k N ( v j ) N I ( v j ) \Delta = I(parent) - \sum_{j=1}^k\frac{N(v_j)}{N}I(v_j) Δ=I(parent)−j=1∑kNN(vj)I(vj)
- I ( ⋅ ) I(·) I(⋅) 给定节点的不纯性度量
- N N N 父节点的记录总数
- k k k 属性值的个数
- N ( v j ) N(v_j) N(vj) 与子女节点 v j v_j vj 相关的记录数
当我们选择熵作为度量时，我们相当于在使用 信息增益
G
A
I
N
s
p
l
i
t
=
E
n
t
r
o
p
y
(
p
)
−
(
∑
i
=
1
k
n
i
n
E
n
t
r
o
p
y
(
i
)
)
GAIN_{split} = Entropy(p) - (\sum_{i=1}^k\frac{n_i}{n}Entropy(i))
GAINsplit=Entropy(p)−(i=1∑knniEntropy(i))
此时父节点
p
p
p 分裂为
k
k
k 个部分，
n
j
n_j
nj 是在第
j
j
j 个部分的样本数量.
衡量了如果产生此分裂，那么我们得到的信息增益是多少。
如果要进行分裂，那么每一次分裂都选择使得
G
A
I
N
GAIN
GAIN 最大的特征。
I D 3 ID3 ID3
- 自上而下地构建决策树
- 每一次都选择一个属性来进行分裂过程
- 分类能力最好的特征作为根节点
- 根节点的每一个可能的值产生一个分支
- 将样本划分到对应的分支中
- 对每一个分支重复进行分裂过程
使用的标准就是信息增益
即
G
A
I
N
s
p
l
i
t
=
E
n
t
r
o
p
y
(
p
)
−
(
∑
i
=
1
k
n
i
n
E
n
t
r
o
p
y
(
i
)
)
GAIN_{split} = Entropy(p) - (\sum_{i=1}^k\frac{n_i}{n}Entropy(i))
GAINsplit=Entropy(p)−(i=1∑knniEntropy(i))
它的特点：
优势：
- 算法理论很清晰
- 方法简单
- 学习能力较强
不足：
- 容易过拟合
- 连续值特征需要改变标准
- 缺失值的处理
- 处理不同代价的特征问题
- G a i n 2 ( S , A ) C o s t ( A ) \frac{Gain^2(S,A)}{Cost(A)} Cost(A)Gain2(S,A)
- 2 G a i n ( S , A ) − 1 ( C o s t ( A ) + 1 ) w \frac{2^{Gain(S,A)}-1}{(Cost(A)+1)^w} (Cost(A)+1)w2Gain(S,A)−1
也可以采用 G i n i I n d e x Gini\ Index Gini Index 来作为度量标准
C 4.5 C4.5 C4.5
C
4
,
5
C4,5
C4,5 算法是针对
I
D
3
ID3
ID3 算法的一种改进。
体现在
- 新的属性划分标准
- 连续值属性的学习问题
- 含缺失值的处理
- 避免树的过度增长，避免过拟合（缓解过拟合）
它是一种监督学习算法，一种归纳学习算法
I D 3 ID3 ID3 中划分标准的问题
- 信息增益度量天然的偏向于具有较多取值的特征
- 举一个极端例子：顾客的 I D ID ID ,每一个顾客都不同，那么根据不纯度标准，模型就会选择这个特征来进行划分，而且一次划分就将所有数据划分完
针对上述问题，我们引入一个惩罚
S
p
l
i
t
I
N
F
O
=
−
∑
i
=
1
k
n
i
n
log
2
n
i
n
SplitINFO = -\sum_{i=1}^k\frac{n_i}{n}\log_2\frac{n_i}{n}
SplitINFO=−i=1∑knnilog2nni
- 惩罚特征取值较多的属性
- 衡量特征分裂数据的广度和均匀性
由此，我们有了一个新的衡量标准：
G a i n R A T I O s p l i t = G A I N s p l i t S p l i t I N F O GainRATIO_{split} = \frac{GAIN_{split}}{SplitINFO} GainRATIOsplit=SplitINFOGAINsplit
连续值的划分问题
- 对每一个连续值特征对取值进行排序
- 利用不同的值进行动态划分
- 选择不同的阈值，将数据划分为两部分
- 计算两部分的信息增益率，选出使其最高的阈值
- 将最高的信息增益率作为与其余特征进行比较的增益率
缺失值
- 抛弃缺失值，但是当缺失值较多时，不能采用这种方法
- 其他方法
- 赋予它节点处样本中最常见的值
- 赋予一个概率分布，不同取值的概率
- 修正增益参数
F
F
F
- F F F 为某特征已知的样本数量 / / / 数据集中样本数量的总和.
- 此时 G A I N n e w = F ∗ G A I N GAIN_{new} = F*GAIN GAINnew=F∗GAIN
- 或者将缺失值当做新的类别，利用原来的标准参与构建模型。
- 赋予每一个子树的样本一个类别概率用来解决缺失值问题。
树的剪枝
为了解决树的过拟合的问题
- 噪声的存在
- 偶然的规律性
剪枝一共有两种
- 预剪枝
及早停止树的增长 - 后剪枝
构建完树后进行修剪
剪枝的标准
- 训练集和验证集法
- 使用所有数据进行训练，但进行统计测试来评估一个节点是否可能改善在训练集外的实例的性能
- 最小描述长度
- 启发式的规则 s i z e ( t r e e ) + s i z e ( m i s c l a s s i f i c a t i o n s ( t r e e ) ) size(tree) + size(misclassifications(tree)) size(tree)+size(misclassifications(tree))
错误率降低修剪 R E P ( R e d u c e d − E r r o r P r u n i n g ) REP(Reduced-Error\ Pruning) REP(Reduced−Error Pruning)
数据分为三个子集
- 训练集，构建决策树
- 验证集，修剪决策树
- 测试集，评估决策树的泛化性能
修剪步骤：
- 删除某节点为根的子树，使其成为叶节点
- 将与该节点关联的样本中最常见的分类赋给他
- 计算错误率，比较修剪前后的错误率
- 每一次都选择删除使得错误率降低最多的节点
- 重复修剪，直到修剪是有害的
预剪枝与后剪枝
- 预剪枝：每一次节点的划分还要考虑当前树在验证集上的错误率情况。
- 后剪枝：构建完树后，进行错误率降低修剪。
C 4 , 5 C4,5 C4,5 剪枝法
- 悲观剪枝 P e s s i m i s t i c E r r o r P r u n i n g , P E P Pessimistic\ Error\ Pruning,PEP Pessimistic Error Pruning,PEP
- 不划分出验证集，利用所有训练数据来剪枝
e
′
(
t
)
=
e
(
t
)
+
1
2
e'(t) = e(t) + \frac{1}{2}
e′(t)=e(t)+21
e
′
(
T
t
)
=
∑
e
(
i
)
+
N
t
2
e'(T_t) = \sum e(i) + \frac{N_t}{2}
e′(Tt)=∑e(i)+2Nt
S
(
e
′
(
T
t
)
)
=
[
e
′
(
T
t
)
n
(
t
)
−
e
′
(
T
t
)
n
(
t
)
]
1
2
S(e'(T_t)) = [e'(T_t)\frac{n(t) - e'(T_t)}{n(t)}]^{\frac{1}{2}}
S(e′(Tt))=[e′(Tt)n(t)n(t)−e′(Tt)]21
如果有
e
′
(
t
)
≤
e
′
(
T
t
)
+
S
(
e
′
(
T
t
)
)
e'(t) \leq e'(T_t) + S(e'(T_t))
e′(t)≤e′(Tt)+S(e′(Tt))
其中
e
(
t
)
e(t)
e(t) 为节点
t
t
t 的误差，
i
i
i 为子树
T
t
T_t
Tt 的节点，
N
t
N_t
Nt 为子树的叶节点数目，
n
t
n_t
nt为节点
t
t
t 包含的样本数。
时，子树
T
t
T_t
Tt 应被剪枝为叶子节点。
C A R T ( C l a s s i f i c a t i o n a n d R e g r e s s i o n T r e e s ) CART\ (Classification\ and\ Regression\ Trees) CART (Classification and Regression Trees)
在 C A R T CART CART 算法中，采用了二元划分，即二叉树。
- 内部节点取值为 是 或者 否
- 左分支为是，右分支为否
- 二叉树的优点
- 不容易产生数据碎片
- 精度往往高于多叉树
即递归的划分每一个属性，在属性空间上划分有限个单元，并确定单元上的预测概率分布。
分裂标准的度量选择 G i n i I n d e x Gini\ Index Gini Index
- 离散，逻辑与之前类似
- 连续，考虑所有可能的分裂点，选出最优的
G i n i A ( D ) = ∑ i = 1 v ∣ D i ∣ D ∗ G i n i ( D i ) Gini_A(D) = \sum_{i=1}^v\frac{|D_i|}{D}*Gini(D_i) GiniA(D)=i=1∑vD∣Di∣∗Gini(Di)
构建树的终止条件：
- 所有叶节点的样本数为1、或者样本数小于某个给定的值，或者样本都属于某一类
- 决策树的高度达到设定的阈值，或者分之后的叶节点的样本特征都属于某一类
- 数据中不再有特征向量作为分支选择的时候
C A R T CART CART 算法
由于 C A R T CART CART 的特点，相较于之前的算法，它有些许不同。
- 设节点的训练数据集为 D D D，计算现有属性对该数据集的 G i n i I n d e x Gini\ Index Gini Index。此时，对每一个属性 A A A,对其每一个的可能取值 a a a,根据样本对 A = a A = a A=a的测试为是或者否将数据集进行划分，并计算此时的 G i n i I n d e x Gini\ Index Gini Index;
- 选择最小的 G i n i I n d e x Gini\ Index Gini Index 作为当前进行分割的标准来进行划分
- 递归进行上述两步，直至满足停止条件
C A R T CART CART 剪枝策略
- C C P ( C o s t − C o m p l e x i t y P r u n i n g ) CCP(Cost-Complexity\ Pruning) CCP(Cost−Complexity Pruning) 代价复杂度剪枝；从树的底端剪去一些子树,使模型变得更加简单，能够具有更高的泛化性能
- 选择节点误差率增益值最小的非叶节点，删除该节点；如果都很小，则删除节点数最多的非叶节点。
- 这个过程会产生一列树 { T 0 , . . . , T n } \{T_0,...,T_n\} {T0,...,Tn}
- 通过交叉验证从上面的集合中选出最优子树
子树的损失函数：
C
α
(
T
)
=
C
(
T
)
+
α
∣
T
∣
C_{\alpha}(T) = C(T) + \alpha |T|
Cα(T)=C(T)+α∣T∣
∣
T
∣
|T|
∣T∣ 代表了子树中的叶节点的数目
具体算法
总结
- 大致记录了一些经典的决策树算法
- I D 3 ID3 ID3 算法搜索完整的假设空间
- I D 3 ID3 ID3 算法优先选择较短的树，通过搜索假设空间来增长树，使得其刚好能够分类已有的训练样例
- 过拟合是树模型需要解决的一个关键问题。剪枝是一种很好的减缓过拟合的方法。
- C 4.5 C4.5 C4.5 算法可以处理连续值属性；可以容纳存在缺失值的样本；使用除了增益率作为标准来选择属性；考虑了剪枝的方法
- C A R T CART CART 可以处理分类和回归问题
扫一扫
776
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
