Dijkstra算法

一、代码

//
// Created by dgm on 19-4-3.
//
#include <iostream>
using namespace std;
#define Maxnum 100
#define Infinity 65535
typedef int Vertex;
typedef int ARType;
typedef char* Info;
typedef struct {
    ARType adj=Infinity;    //边长
    Info info;
}Arcs[Maxnum][Maxnum];      //arcs[i][j]表示顶点i到j的边长

typedef struct {
    Arcs arcs;
    Vertex vexs[Maxnum];//顶点编号，简单起见，从0开始编号
    int arcnum,vexnum;
}MGraph;

void CreateMGraph(MGraph&G)
{
    cin>>G.vexnum>>G.arcnum;    //顶点数和边数
    for (int i = 0; i < G.vexnum; ++i) cin>>G.vexs[i];
    int posx,posy,weight;   //边的起点终点和权值
    for (int i = 0; i < G.arcnum; ++i) {
        cin>>posx>>posy>>weight;
        G.arcs[posx][posy].adj=weight;
    }
}

typedef int PathMatrix[Maxnum][Maxnum];
typedef int ShortPathTable[Maxnum];

void ShortestPath_Dijkstra(MGraph G,int v0,PathMatrix&P,ShortPathTable&D)
{
    //D[i]表示从v0到i的最短路径长度，
    //P[j][w]=1表示顶点w位于从v0到j的最短路径上
    bool final[Maxnum];//final[j]=true表示从v0到j的最短路径已经建立
    int v;
    for (int i = 0; i < G.vexnum; ++i) {
        final[i]= false;
        D[i]=G.arcs[v0][i].adj;//初始化v0到各顶点的距离
        for (int j = 0; j < G.vexnum; ++j) P[i][j]=0;//初始化路径
        if(D[i]<Infinity)//如果v0与i之间有边
        {
            P[i][v0]=1;P[i][i]=1;//暂时建立路径v0->i（接下来会根据路径长短更新）
        }
    }
    final[v0]= true;D[v0]=0;//v0到v0的最短路径是0
    for (int i = 1; i < G.vexnum; ++i) {
        int min=Infinity;
        for (int j = 0; j < G.vexnum; ++j) {
            if (!final[j]&&(D[j]<min)){
                min=D[j];v=j;//找到距离v0最近且未加入最短路径的那个点，用v记录下来
            }
        }
        final[v]=true;//将v加入最短路径
        for (int j = 0; j < G.vexnum; ++j) {//建立v0与v的最短路径后，
                // 更新v0到尚未与v0建立最短路径的各点的距离（最短距离）
            if (!final[j]&&(min+G.arcs[v][j].adj<D[j]))
            {
                D[j]=min+G.arcs[v][j].adj;//如果v0->v->j的长度小于v0->j
                //那么从v0到j的路径更新为从v0到v的路径+从v到j的路径
                for (int k = 0; k < G.vexnum; ++k) P[j][k]=P[v][k];
                P[j][j]= 1;
            }
        }
    }//for循环一次，就会建立一条v0到其他顶点的最短路径，
    // final一直在变化，当所有顶点的final值都为true时，到每一个顶点的最短路径也就建立了
}

int main()
{
    MGraph G;
    CreateMGraph(G);
    ShortPathTable D;
    PathMatrix P;
    ShortestPath_Dijkstra(G,0,P,D);
    for (int i = 0; i < G.vexnum; ++i) {
        cout<<i<<": ";
        for (int j = 0; j < G.vexnum&&j!=i; ++j)
            //P[i][j]=1表示j在从v0到i的最短路径上
            if (P[i][j]==1) cout<<j<<"->";
            cout<<i<<"  ";
        cout<<"shortest path: "<<D[i]<<endl;
    }
    return 0;
}

输入及输出：

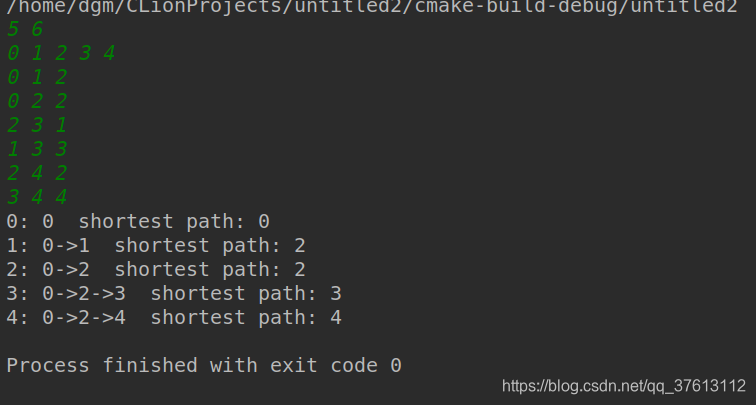
二、过程

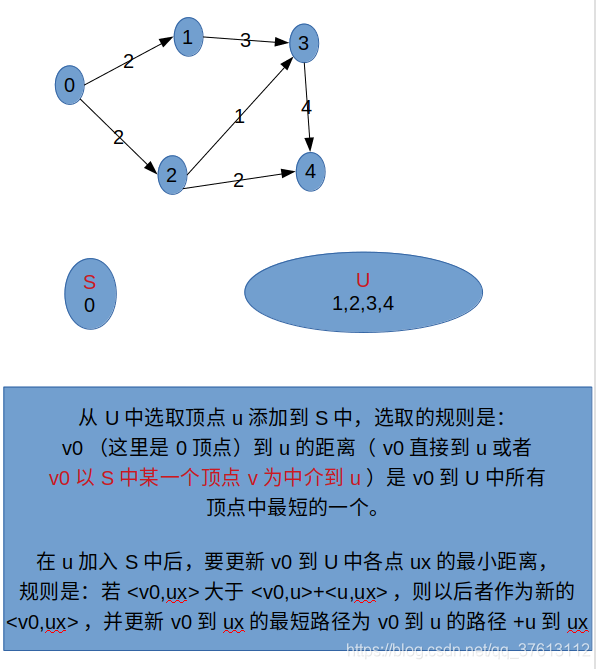
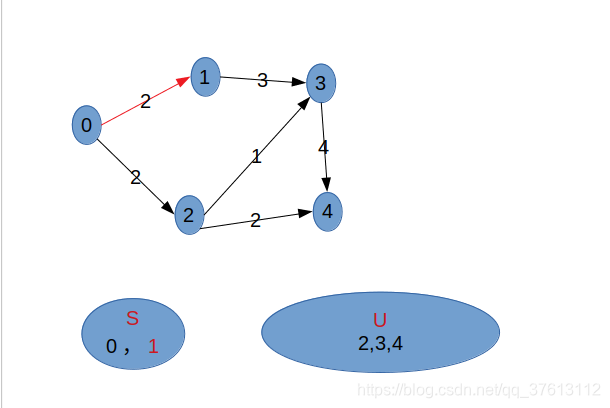
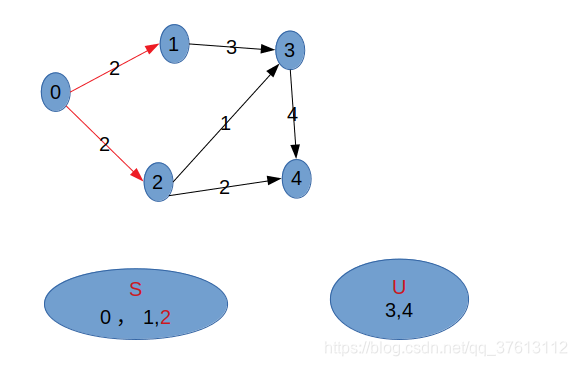
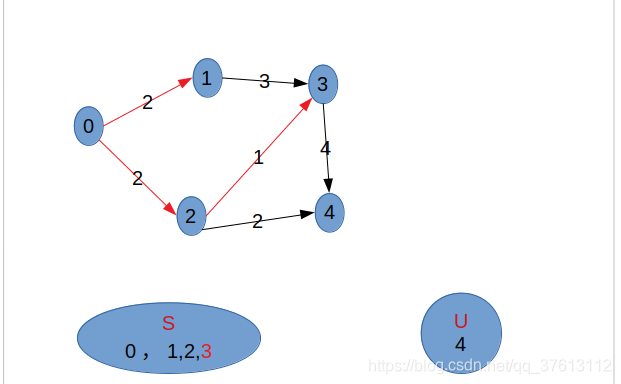
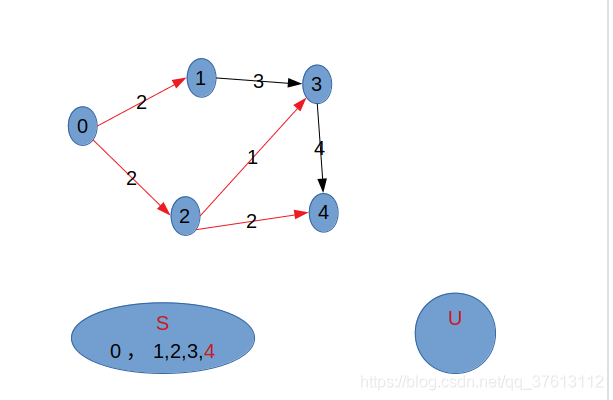
总结

dijkstra算法与prim算法非常相似：
prim算法是不断寻找U中与集合S之间距离最小的顶点加入S中（相当于集合与集合的最小距离），而dijsktra算法是不断寻找U中与集合S中的v0顶点之间距离最小的顶点加入S中（相当于点与集合的最小距离）。个人认为主要的两步是：①、找U（不属于最小生成树/最短路径集合的顶点）中距离（S/v0）最小的顶点并加入到S中；②、更新S/v0到U中其余点的距离。