【算法】计算时间复杂度

• O(n) 小于等于

• o(n) 小于

• Ω(n) 大于等于

• ω(n) 大于

• Θ(n) 等于

直接判断时间复杂度

• Q1：

其中，所以f is in Θ(n)

• Q2：

其中，所以f is in O(n)

根据代码判断时间复杂度

 

声明：Python len()的时间复杂度为O(1)

def first_or_last(numbers):
    n = len(numbers)
    return numbers[0] + numbers[n - 1]

• Q1：O(1)

def filter(numbers):
    result = []
    for x in numbers:
        if x >= 0:
            result.append(x)
    return result

• Q2：O(n)

def nested(nums):
    n = len(nums)
    c = 0
    for i in range(n):
        for j in range(i * i):
            c += 1
    return c

• Q3：O(n^3)

def dumbo_func(data):
    if len(data) == 0:
        return 0
    else:
        if (data[0] // 100) % 3 != 0:
            return 1 + dumbo_func(data[1:])
        else:
            return dumbo_func(data[1:])

• Q4：O(n^2)：原因是递归的深度是k=n，且slicing(切片)的时间复杂度是O(n)

def fiddling(numbers):
    m = len(numbers)
    while m > 5:
        m = m // 2
    return m

• Q5：O(logn)

---

def mysum(A):
    if len(A) == 0:
        return 0
    else:
        return A[0] + mysum(A[1:])

 

• The number of nodes at depth d is 1 (每一层只有一个点)
• The cost expression for each node at depth d is c(n-d) (每一层都是A[x:])
• The sum of costs for all the nodes at depth d is c(n-d) (A[x:])
• The depth of the recurrence tree is O(n) (从A[1:]就可以知道深度为n)
• The running time complexity of the algorithm is O(n^2) (递归的深度是k=n，且slicing(切片)的时间复杂度是O(n))

根据递推式计算时间复杂度

• Q1：上述代码的递推式

    

---

• Q2：

    

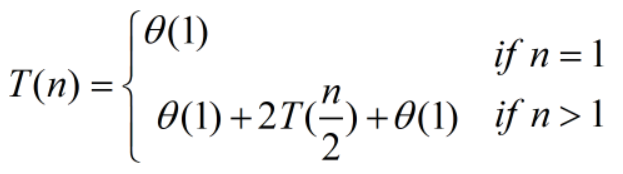
• The number of nodes at depth d is 2^d
• The cost expression for each node at depth d is c
• The sum of costs for all the nodes at depth d is c(2^d)
• The depth of the recurrence tree is in O(logn)
• The running time complexity of the algorithm is O(n)